
En relatividad , la velocidad propia (también conocida como celeridad ) w de un objeto en relación con un observador es la relación entre el vector de desplazamiento medido por el observador y el tiempo propio τ transcurrido en los relojes del objeto en viaje:
Es una alternativa a la velocidad ordinaria , la distancia por unidad de tiempo donde tanto la distancia como el tiempo son medidos por el observador.
Los dos tipos de velocidad, ordinaria y propia, son casi iguales a bajas velocidades. Sin embargo, a altas velocidades, la velocidad propia conserva muchas de las propiedades que la velocidad pierde en la relatividad en comparación con la teoría newtoniana . Por ejemplo, la velocidad propia es igual al momento por unidad de masa a cualquier velocidad y, por lo tanto, no tiene límite superior. A altas velocidades, como se muestra en la figura de la derecha, también es proporcional a la energía de un objeto.
La velocidad propia w se puede relacionar con la velocidad ordinaria v a través del factor de Lorentz γ :
donde t es el tiempo de coordenadas o "tiempo del mapa". Para el movimiento unidireccional, cada uno de estos también está relacionado simplemente con el ángulo de velocidad hiperbólica o la rapidez η de un objeto en movimiento mediante
En el espacio-tiempo plano , la velocidad propia es la relación entre la distancia recorrida en relación con un marco de mapa de referencia (usado para definir la simultaneidad) y el tiempo propio τ transcurrido en los relojes del objeto en movimiento. Es igual al momento del objeto p dividido por su masa en reposo m , y está formada por los componentes espaciales de la velocidad de cuatro vectores del objeto . La monografía de William Shurcliff [1] mencionó su uso temprano en el texto de Sears y Brehme. [2] Fraundorf ha explorado su valor pedagógico [3] mientras que Ungar, [4] Baylis [5] y Hestenes [6] han examinado su relevancia desde las perspectivas de la teoría de grupos y el álgebra geométrica . A la velocidad propia a veces se la denomina celeridad. [7]

A diferencia de la velocidad de coordenadas más conocida v , la velocidad propia no tiene sincronía [1] (no requiere relojes sincronizados) y es útil para describir tanto el movimiento superrelativista como el subrelativista. Al igual que la velocidad de coordenadas y a diferencia de la velocidad de cuatro vectores, reside en la porción tridimensional del espacio-tiempo definida por el marco del mapa. Como se muestra a continuación y en la figura de ejemplo a la derecha, las velocidades propias incluso se suman como tres vectores con el reescalado del componente fuera del marco. Esto las hace más útiles para aplicaciones basadas en mapas (por ejemplo, ingeniería) y menos útiles para obtener información sin coordenadas. La velocidad propia dividida por la velocidad de la luz c es el seno hiperbólico de la rapidez η , así como el factor de Lorentz γ es el coseno hiperbólico de la rapidez, y la velocidad de coordenadas v sobre la velocidad de la luz es la tangente hiperbólica de la rapidez.
Imaginemos un objeto que viaja a través de una región del espacio-tiempo descrita localmente por la ecuación métrica del espacio plano de Hermann Minkowski ( cdτ ) 2 = ( cd t) 2 − ( d x ) 2 . Aquí un marco de mapa de referencia de varas y relojes sincronizados definen la posición del mapa x y el tiempo del mapa t respectivamente, y la d que precede a una coordenada significa un cambio infinitesimal. Un poco de manipulación permite demostrar que la velocidad propia w = d x / dτ = γ v donde como es habitual la velocidad de las coordenadas v = d x / dt . Así, la w finita asegura que v sea menor que la velocidad de la luz c . Al agrupar γ con v en la expresión para el momento relativista p , la velocidad propia también extiende la forma newtoniana del momento como masa por velocidad a altas velocidades sin necesidad de masa relativista . [8]
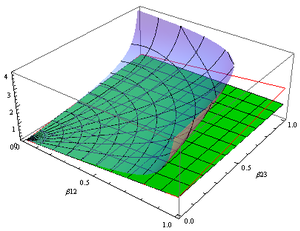
La fórmula adecuada para la adición de velocidades: [9] [10] [4]
donde es el factor beta dado por .
Esta fórmula proporciona un modelo de espacio girovectorial de velocidad adecuado para la geometría hiperbólica que utiliza un espacio completo en comparación con otros modelos de geometría hiperbólica que utilizan discos o semiplanos.
En el caso unidireccional, esto se vuelve conmutativo y se simplifica a un producto de factor de Lorentz por una suma de velocidad de coordenadas, por ejemplo, w AC = γ AB γ BC ( v AB + v BC ) , como se analiza en la sección de aplicación a continuación.
La siguiente tabla ilustra cómo la velocidad adecuada de w = c o "un año luz de mapa por año-viajero" es un punto de referencia natural para la transición del movimiento subrelativista al superrelativista.
Nótese que, como se muestra arriba, el ángulo de velocidad η y la velocidad propia w van de 0 a infinito y siguen la velocidad de coordenadas cuando w << c . Por otro lado, cuando w >> c , la velocidad propia sigue el factor de Lorentz, mientras que el ángulo de velocidad es logarítmico y, por lo tanto, aumenta mucho más lentamente.
Las siguientes ecuaciones convierten entre cuatro medidas alternativas de velocidad (o velocidad unidireccional) que surgen de la ecuación métrica del espacio plano de Minkowski:
o en términos de logaritmos:
La velocidad propia es útil para comparar la velocidad de los objetos con un momento por unidad de masa en reposo ( w ) mayor que la velocidad de la luz c . La velocidad de coordenadas de dichos objetos es generalmente cercana a la velocidad de la luz, mientras que la velocidad propia indica la rapidez con la que cubren terreno en los relojes de objetos en movimiento . Esto es importante, por ejemplo, si, como algunas partículas de rayos cósmicos, los objetos en movimiento tienen una vida útil finita. La velocidad propia también nos da pistas sobre el momento del objeto, que no tiene límite superior.
Por ejemplo, un electrón de 45 GeV acelerado por el Gran Colisionador de Electrones y Positrones (LEP) en el CERN en 1989 habría tenido un factor de Lorentz γ de aproximadamente 88.000 (45 GeV dividido por la masa en reposo del electrón de 511 keV). Su velocidad de coordenadas v habría sido aproximadamente sesenta y cuatro billonésimas menor que la velocidad de la luz c a 1 segundo luz por segundo de mapa . Por otro lado, su velocidad propia habría sido w = γv ~ 88.000 segundos luz por segundo viajero . En comparación, la velocidad de coordenadas de un electrón de 250 GeV en el Colisionador Lineal Internacional propuesto [11] (ILC) permanecerá cerca de c , mientras que su velocidad propia aumentará significativamente a ~489.000 segundos luz por segundo viajero.
La velocidad propia también es útil para comparar velocidades relativas a lo largo de una línea a alta velocidad. En este caso
donde A, B y C se refieren a diferentes objetos o marcos de referencia. [12] Por ejemplo, w AC se refiere a la velocidad propia del objeto A con respecto al objeto C. Por lo tanto, al calcular la velocidad propia relativa, los factores de Lorentz se multiplican cuando las velocidades de las coordenadas se suman.
Por lo tanto, cada uno de los dos electrones (A y C) en una colisión frontal a 45 GeV en el marco de referencia de laboratorio (B) vería al otro acercándose a ellos a v AC ~ c y w AC = 88.000 2 (1 + 1) ~ 1,55×10 10 segundos luz por segundo viajero. Por lo tanto, desde el punto de vista del objetivo, los colisionadores pueden explorar colisiones con una energía de proyectil y un momento por unidad de masa mucho mayores.

Al representar gráficamente "( γ − 1) en función de la velocidad propia" después de multiplicar la primera por mc2 y la segunda por la masa m , para distintos valores de m, se obtiene una familia de curvas de energía cinética en función del momento que incluye la mayoría de los objetos en movimiento que encontramos en la vida cotidiana. Tales gráficos se pueden utilizar, por ejemplo, para mostrar dónde figuran la velocidad de la luz, la constante de Planck y la energía de Boltzmann kT .
Para ilustrarlo, la figura de la derecha con ejes logarítmicos muestra objetos con la misma energía cinética (relacionados horizontalmente) que tienen diferentes cantidades de momento, así como también cómo se compara la velocidad de un objeto de baja masa (por extrapolación vertical) con la velocidad después de una colisión perfectamente inelástica con un objeto grande en reposo. Las líneas con una pendiente muy pronunciada (elevación/recorrido = 2) marcan los contornos de masa constante, mientras que las líneas con una pendiente unitaria marcan los contornos de velocidad constante.
Los objetos que encajan bien en esta trama son los humanos conduciendo automóviles, las partículas de polvo en movimiento browniano , una nave espacial en órbita alrededor del Sol, moléculas a temperatura ambiente, un avión de combate a Mach 3, un fotón de onda de radio , una persona que se mueve a un año luz por año viajero, el pulso de un láser de 1,8 MegaJoule , un electrón de 250 GeV y nuestro universo observable con la energía cinética del cuerpo negro esperada de una sola partícula a 3 kelvin.
La aceleración propia a cualquier velocidad es la aceleración física que experimenta localmente un objeto . En el espacio-tiempo es una aceleración de tres vectores con respecto al marco de referencia de flotación libre que varía instantáneamente del objeto. [13] Su magnitud α es la magnitud invariante en el marco de referencia de la aceleración de cuatro vectores de ese objeto . La aceleración propia también es útil desde el punto de vista (o porción de espacio-tiempo) de los observadores externos. No solo los observadores en todos los marcos de referencia pueden estar de acuerdo sobre su magnitud, sino que también mide hasta qué punto un cohete en aceleración "tiene el acelerador a fondo".
En el caso unidireccional, es decir, cuando la aceleración del objeto es paralela o antiparalela a su velocidad en la porción de espacio-tiempo del observador, el cambio en la velocidad propia es la integral de la aceleración propia sobre el tiempo del mapa, es decir, Δ w = α Δ t para α constante . A bajas velocidades, esto se reduce a la relación bien conocida entre la velocidad de las coordenadas y la aceleración de las coordenadas por el tiempo del mapa, es decir, Δ v = a Δ t . Para una aceleración propia unidireccional constante, existen relaciones similares entre la rapidez η y el tiempo propio transcurrido Δ τ , así como entre el factor de Lorentz γ y la distancia recorrida Δ x . Para ser más específicos:
donde como se señaló anteriormente los diversos parámetros de velocidad están relacionados por
Estas ecuaciones describen algunas consecuencias de viajar acelerado a alta velocidad. Por ejemplo, imaginemos una nave espacial que puede acelerar a sus pasajeros a 1 g (o 1,03 años luz/año 2 ) hasta la mitad del camino hacia su destino, y luego desacelerarlos a 1 g durante la mitad restante para proporcionar gravedad artificial similar a la de la Tierra desde el punto A al punto B en el menor tiempo posible. Para una distancia cartográfica de Δx AB , la primera ecuación anterior predice un factor de Lorentz de punto medio (por encima de su valor de reposo unitario) de γ mid = 1 + α (Δ x AB /2)/ c 2 . Por lo tanto, el tiempo de ida y vuelta en los relojes de los viajeros será Δ τ = 4( c / α )cosh −1 [ γ mid ], durante el cual el tiempo transcurrido en los relojes cartográficos será Δ t = 4( c / α )sinh[cosh −1 [ γ mid ]].

Esta nave espacial imaginaria podría ofrecer viajes de ida y vuelta a Próxima Centauri con una duración de unos 7,1 años-viajero (unos 12 años en los relojes de la Tierra), viajes de ida y vuelta al agujero negro central de la Vía Láctea de unos 40 años (unos 54.000 años transcurridos en los relojes de la Tierra) y viajes de ida y vuelta a la galaxia de Andrómeda con una duración de unos 57 años (más de 5 millones de años en los relojes de la Tierra). Desafortunadamente, aunque se pueden alcanzar fácilmente aceleraciones de 1 g en cohetes, no se pueden mantener durante largos períodos de tiempo. [14]