En la ciencia de los materiales , la dureza (antónimo: suavidad ) es una medida de la resistencia a la deformación plástica localizada , como una hendidura (sobre un área) o un rasguño (lineal), inducida mecánicamente ya sea por presión o abrasión . En general, los diferentes materiales difieren en su dureza; por ejemplo, los metales duros como el titanio y el berilio son más duros que los metales blandos como el sodio y el estaño metálico , o la madera y los plásticos comunes . La dureza macroscópica generalmente se caracteriza por fuertes enlaces intermoleculares , pero el comportamiento de los materiales sólidos bajo fuerza es complejo; por lo tanto, la dureza se puede medir de diferentes maneras, como la dureza al rayado , la dureza por hendidura y la dureza de rebote. La dureza depende de la ductilidad , la rigidez elástica , la plasticidad , la deformación , la resistencia , la tenacidad , la viscoelasticidad y la viscosidad . Los ejemplos comunes de materia dura son la cerámica , el hormigón , ciertos metales y los materiales superduros , que pueden contrastarse con la materia blanda .

Existen tres tipos principales de medidas de dureza: rayado, indentación y rebote. Dentro de cada una de estas clases de medida existen escalas de medición individuales. Por razones prácticas se utilizan tablas de conversión para convertir entre una escala y otra.
La dureza al rayado es la medida de la resistencia de una muestra a la fractura o deformación plástica permanente debido a la fricción de un objeto afilado. [1] El principio es que un objeto hecho de un material más duro rayará un objeto hecho de un material más blando. Al probar recubrimientos, la dureza al rayado se refiere a la fuerza necesaria para cortar la película hasta el sustrato. La prueba más común es la escala de Mohs , que se utiliza en mineralogía . Una herramienta para realizar esta medición es el esclerómetro .
Otra herramienta que se utiliza para realizar estas pruebas es el durómetro de bolsillo . Esta herramienta consta de un brazo de escala con marcas graduadas unido a un carro de cuatro ruedas. Una herramienta de rayado con un borde afilado se monta en un ángulo predeterminado con respecto a la superficie de prueba. Para utilizarla, se añade un peso de masa conocida al brazo de escala en una de las marcas graduadas y luego se pasa la herramienta por la superficie de prueba. El uso del peso y las marcas permite aplicar una presión conocida sin necesidad de maquinaria complicada. [2]
La dureza por indentación mide la resistencia de una muestra a la deformación del material debido a una carga de compresión constante de un objeto afilado. Las pruebas de dureza por indentación se utilizan principalmente en ingeniería y metalurgia . Las pruebas funcionan sobre la premisa básica de medir las dimensiones críticas de una indentación dejada por un indentador específicamente dimensionado y cargado. Las escalas de dureza por indentación más comunes son Rockwell , Vickers , Shore y Brinell , entre otras.
La dureza de rebote , también conocida como dureza dinámica , mide la altura del "rebote" de un martillo con punta de diamante que se deja caer desde una altura fija sobre un material. Este tipo de dureza está relacionada con la elasticidad . El dispositivo utilizado para tomar esta medida se conoce como escleroscopio . [3] Dos escalas que miden la dureza de rebote son la prueba de dureza de rebote de Leeb y la escala de dureza de Bennett. El método de impedancia de contacto ultrasónico (UCI) determina la dureza midiendo la frecuencia de una varilla oscilante. La varilla consta de un eje de metal con un elemento vibratorio y un diamante en forma de pirámide montado en un extremo. [4]
Hay cinco procesos de endurecimiento: fortalecimiento de Hall-Petch , endurecimiento por trabajo , fortalecimiento por solución sólida , endurecimiento por precipitación y transformación martensítica .

En mecánica de sólidos , los sólidos generalmente tienen tres respuestas a la fuerza , dependiendo de la cantidad de fuerza y el tipo de material:
La resistencia es una medida del alcance del rango elástico de un material, o de los rangos elástico y plástico juntos. Esto se cuantifica como resistencia a la compresión , resistencia al corte y resistencia a la tracción según la dirección de las fuerzas involucradas. La resistencia máxima es una medida de ingeniería de la carga máxima que puede soportar una parte de un material y una geometría específicos.
La fragilidad , en el uso técnico, es la tendencia de un material a fracturarse con muy poca o ninguna deformación plástica detectable de antemano. Por lo tanto, en términos técnicos, un material puede ser frágil y fuerte. En el uso cotidiano, "fragilidad" generalmente se refiere a la tendencia a fracturarse bajo una pequeña cantidad de fuerza, lo que muestra tanto fragilidad como falta de resistencia (en el sentido técnico). Para materiales perfectamente frágiles, el límite elástico y la resistencia máxima son los mismos, porque no experimentan una deformación plástica detectable. Lo opuesto a la fragilidad es la ductilidad .
La tenacidad de un material es la cantidad máxima de energía que puede absorber antes de fracturarse, que es diferente de la cantidad de fuerza que se puede aplicar. La tenacidad tiende a ser pequeña en el caso de los materiales frágiles, porque las deformaciones elásticas y plásticas permiten que los materiales absorban grandes cantidades de energía.
La dureza aumenta a medida que disminuye el tamaño de las partículas . Esto se conoce como efecto Hall-Petch . Sin embargo, por debajo de un tamaño de grano crítico, la dureza disminuye a medida que disminuye el tamaño de grano. Esto se conoce como efecto Hall-Petch inverso.
La dureza de un material a la deformación depende de su microdurabilidad o módulo de corte a pequeña escala en cualquier dirección, no de ninguna propiedad de rigidez como su módulo volumétrico o módulo de Young . La rigidez a menudo se confunde con la dureza. [5] [6] Algunos materiales son más rígidos que el diamante (por ejemplo, el osmio) , pero no son más duros y son propensos a descascarillarse y descascararse en hábitos escamosos o aciculares.

La clave para entender el mecanismo que subyace a la dureza es comprender la microestructura metálica , o la estructura y disposición de los átomos a nivel atómico. De hecho, la mayoría de las propiedades metálicas más importantes que son fundamentales para la fabricación de los bienes actuales están determinadas por la microestructura de un material. [7] A nivel atómico, los átomos de un metal están dispuestos en una matriz tridimensional ordenada llamada red cristalina . Sin embargo, en realidad, es probable que una muestra dada de un metal nunca contenga una red cristalina única consistente. Una muestra dada de metal contendrá muchos granos, y cada grano tendrá un patrón de matriz bastante consistente. A una escala aún más pequeña, cada grano contiene irregularidades.
Existen dos tipos de irregularidades a nivel de grano de la microestructura que son responsables de la dureza del material. Estas irregularidades son defectos puntuales y defectos lineales. Un defecto puntual es una irregularidad ubicada en un solo sitio de la red dentro de la red tridimensional general del grano. Hay tres defectos puntuales principales. Si falta un átomo en la matriz, se forma un defecto de vacancia . Si hay un tipo diferente de átomo en el sitio de la red que normalmente debería estar ocupado por un átomo de metal, se forma un defecto de sustitución. Si existe un átomo en un sitio donde normalmente no debería estar, se forma un defecto intersticial . Esto es posible porque existe espacio entre los átomos en una red cristalina. Mientras que los defectos puntuales son irregularidades en un solo sitio en la red cristalina, los defectos lineales son irregularidades en un plano de átomos. Las dislocaciones son un tipo de defecto lineal que implica la desalineación de estos planos. En el caso de una dislocación de borde, un medio plano de átomos se encaja entre dos planos de átomos. En el caso de una dislocación helicoidal, dos planos de átomos están desplazados con una disposición helicoidal que corre entre ellos. [8]
En los vidrios, la dureza parece depender linealmente del número de restricciones topológicas que actúan entre los átomos de la red. [9] Por lo tanto, la teoría de la rigidez ha permitido predecir valores de dureza con respecto a la composición.
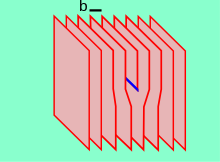
Las dislocaciones proporcionan un mecanismo para que los planos de átomos se deslicen y, por lo tanto, un método para la deformación plástica o permanente. [7] Los planos de átomos pueden voltearse de un lado a otro de la dislocación, lo que permite que la dislocación atraviese el material y que este se deforme de forma permanente. El movimiento permitido por estas dislocaciones provoca una disminución de la dureza del material.
La forma de inhibir el movimiento de los planos de átomos, y por lo tanto hacerlos más duros, implica la interacción de las dislocaciones entre sí y con los átomos intersticiales. Cuando una dislocación se cruza con una segunda dislocación, ya no puede atravesar la red cristalina. La intersección de dislocaciones crea un punto de anclaje y no permite que los planos de átomos continúen deslizándose uno sobre el otro [10] . Una dislocación también puede anclarse mediante la interacción con átomos intersticiales. Si una dislocación entra en contacto con dos o más átomos intersticiales, el deslizamiento de los planos se interrumpirá nuevamente. Los átomos intersticiales crean puntos de anclaje, o puntos de fijación, de la misma manera que las dislocaciones que se cruzan.
Al variar la presencia de átomos intersticiales y la densidad de dislocaciones, se puede controlar la dureza de un metal en particular. Aunque parezca contradictorio, a medida que aumenta la densidad de dislocaciones, se crean más intersecciones y, en consecuencia, más puntos de anclaje. De manera similar, a medida que se agregan más átomos intersticiales, se forman más puntos de fijación que impiden los movimientos de las dislocaciones. Como resultado, cuantos más puntos de anclaje se agreguen, más duro se volverá el material.
Se debe tomar nota cuidadosa de la relación entre un número de dureza y la curva de tensión-deformación exhibida por el material. Esta última, que se obtiene convencionalmente a través de pruebas de tracción , captura la respuesta de plasticidad completa del material (que en la mayoría de los casos es un metal). De hecho, es una dependencia de la (verdadera) deformación plástica de von Mises en la (verdadera) tensión de von Mises , pero esto se obtiene fácilmente a partir de una curva de tensión nominal-deformación nominal (en el régimen de pre- estrechamiento ), que es el resultado inmediato de una prueba de tracción. Esta relación se puede utilizar para describir cómo responderá el material a casi cualquier situación de carga, a menudo utilizando el método de elementos finitos (FEM). Esto se aplica al resultado de una prueba de indentación (con un tamaño y forma determinados de penetrador, y una carga aplicada determinada).
Sin embargo, aunque un número de dureza depende de la relación tensión-deformación, inferir esta última a partir de la primera dista mucho de ser sencillo y no se intenta de ninguna manera rigurosa durante las pruebas de dureza convencionales. (De hecho, la técnica de plastometría de indentación , que implica el modelado iterativo de elementos finitos de una prueba de indentación, permite obtener una curva de tensión-deformación a través de la indentación, pero esto está fuera del alcance de las pruebas de dureza convencionales). Un número de dureza es simplemente un indicador semicuantitativo de la resistencia a la deformación plástica. Aunque la dureza se define de manera similar para la mayoría de los tipos de prueba (normalmente como la carga dividida por el área de contacto), los números obtenidos para un material en particular son diferentes para diferentes tipos de prueba, e incluso para la misma prueba con diferentes cargas aplicadas. En ocasiones se han hecho intentos [11] [12] [13] [14] [15] de identificar expresiones analíticas simples que permitan obtener características de la curva de esfuerzo-deformación, en particular el límite elástico y el límite de tracción (UTS), a partir de un tipo particular de número de dureza. Sin embargo, todos estos intentos se basan en correlaciones empíricas, a menudo específicas de tipos particulares de aleación: incluso con esta limitación, los valores obtenidos suelen ser bastante poco fiables. El problema subyacente es que los metales con una gama de combinaciones de características de límite elástico y endurecimiento por deformación pueden presentar el mismo número de dureza. El uso de números de dureza para cualquier propósito cuantitativo debe, en el mejor de los casos, abordarse con considerable cautela.