Biholomorfismo

Función holomorfa biyectiva con inversa holomorfa

La función exponencial compleja que mapea biholomórficamente un rectángulo a un cuarto de anillo .

En la teoría matemática de funciones de una o más variables complejas , y también en la geometría algebraica compleja , un biholomorfismo o función biholomorfa es una función holomorfa biyectiva cuya inversa también es holomorfa .

Definicion formal

Formalmente, una función biholomórfica es una función definida en un subconjunto abierto U del espacio complejo dimensional C ⁿ con valores en C ⁿ que es holomórfico y uno a uno , de modo que su imagen es un conjunto abierto en C ⁿ y la La inversa también es holomorfa . De manera más general, U y V pueden ser variedades complejas . Como en el caso de funciones de una sola variable compleja, una condición suficiente para que un mapa holomorfo sea biholomórfico en su imagen es que el mapa sea inyectivo, en cuyo caso la inversa también es holomorfa (por ejemplo, ver Gunning 1990, Teorema I. 11 o Corolario E.10 pág. 57). ${\displaystyle \phi }$ ${\displaystyle n}$ ${\displaystyle V}$ ${\displaystyle \phi ^{-1}:V\to U}$

Si existe un biholomorfismo , decimos que U y V son biholomorfismo equivalente o que son biholomorfismo . ${\displaystyle \phi \colon U\to V}$

Teorema de mapeo de Riemann y generalizaciones

Si todo conjunto abierto simplemente conexo que no sea el plano complejo completo es biholomórfico con respecto al disco unitario (este es el teorema de mapeo de Riemann ). La situación es muy diferente en dimensiones superiores. Por ejemplo, las bolas unitarias abiertas y los polidiscos unitarios abiertos no son biholomórficamente equivalentes. De hecho, ni siquiera existe una función holomorfa adecuada de una a otra. ${\displaystyle n=1,}$ ${\displaystyle n>1.}$

Definiciones alternativas

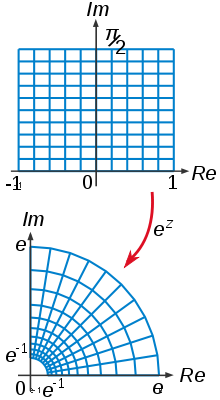
En el caso de aplicaciones f  : U → C definidas en un subconjunto abierto U del plano complejo C , algunos autores (por ejemplo, Freitag 2009, Definición IV.4.1) definen una aplicación conforme como una aplicación inyectiva con derivada distinta de cero, es decir, f '( z )≠ 0 para cada z en U . Según esta definición, un mapa f  : U → C es conforme si y sólo si f : U → f ( U ) es biholomórfico. Tenga en cuenta que, según la definición de biholomorfismos, no se supone nada acerca de sus derivadas, por lo que esta equivalencia contiene la afirmación de que un homeomorfismo que es diferenciable complejo en realidad debe tener una derivada distinta de cero en todas partes. Otros autores (por ejemplo, Conway 1978) definen un mapa conforme como uno con derivada distinta de cero, pero sin requerir que el mapa sea inyectivo. Según esta definición más débil, un mapa conforme no tiene por qué ser biholomórfico, aunque sea localmente biholomórfico, por ejemplo, según el teorema de la función inversa. Por ejemplo, si f : U → U se define por f ( z ) = z ² con U = C –{0}, entonces f es conforme a U , ya que su derivada f '( z ) = 2 z ≠ 0, pero no es biholomórfico, ya que es 2-1.

Referencias

• Conway, John B. (1978). Funciones de una variable compleja . Springer-Verlag. ISBN 3-540-90328-3.
• D'Angelo, John P. (1993). Varias variables complejas y la geometría de hipersuperficies reales . Prensa CRC. ISBN 0-8493-8272-6.
• Freitag, Eberhard; Busam, Rolf (2009). Análisis complejo . Springer-Verlag. ISBN 978-3-540-93982-5.
• Armado, Robert C. (1990). Introducción a las funciones holomorfas de varias variables, vol. II . Wadsworth. ISBN 0-534-13309-6.
• Krantz, Steven G. (2002). Teoría de funciones de varias variables complejas . Sociedad Matemática Estadounidense. ISBN 0-8218-2724-3.

Este artículo incorpora material biholomórficamente equivalente en PlanetMath , que tiene la licencia Creative Commons Attribution/Share-Alike License .