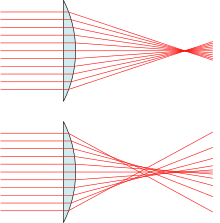

En óptica , la aberración esférica ( SA ) es un tipo de aberración que se encuentra en los sistemas ópticos que tienen elementos con superficies esféricas . Este fenómeno afecta comúnmente a lentes y espejos curvos , ya que estos componentes a menudo tienen forma esférica para facilitar su fabricación. Los rayos de luz que inciden en una superficie esférica fuera del centro se refractan o reflejan más o menos que los que inciden cerca del centro. Esta desviación reduce la calidad de las imágenes producidas por los sistemas ópticos. El efecto de la aberración esférica fue identificado por primera vez en el siglo XI por Ibn al-Haytham, quien lo analizó en su obra Kitāb al-Manāẓir . [1]
Una lente esférica tiene un punto aplanático (es decir, sin aberración esférica) solo a una distancia lateral del eje óptico que es igual al radio de la superficie esférica dividido por el índice de refracción del material de la lente.
La aberración esférica hace que el enfoque de los telescopios y otros instrumentos no sea el ideal. Este es un efecto importante, porque las formas esféricas son mucho más fáciles de producir que las asféricas. En muchos casos, es más barato utilizar múltiples elementos esféricos para compensar la aberración esférica que utilizar una sola lente asférica .
La aberración esférica "positiva" significa que los rayos cerca del borde exterior de una lente se desvían más de lo que se predice para una lente ideal. La aberración esférica "negativa" significa que dichos rayos se desvían menos de lo que se predice.
El efecto es proporcional a la cuarta potencia del diámetro e inversamente proporcional a la tercera potencia de la distancia focal, por lo que es mucho más pronunciado en relaciones focales cortas , es decir, lentes "rápidas".

En los sistemas de lentes, las aberraciones se pueden minimizar utilizando combinaciones de lentes convexas y cóncavas , o utilizando lentes asféricas o lentes aplanáticas.
Los sistemas de lentes con corrección de aberración se diseñan generalmente mediante trazado numérico de rayos . Para diseños simples, a veces se pueden calcular analíticamente parámetros que minimizan la aberración esférica. Por ejemplo, en un diseño que consiste en una sola lente con superficies esféricas y una distancia al objeto o , una distancia a la imagen i y un índice de refracción n dados , se puede minimizar la aberración esférica ajustando los radios de curvatura y de las superficies frontal y posterior de la lente de tal manera que

Para telescopios pequeños que utilizan espejos esféricos con relaciones focales más cortas quef /10, la luz de una fuente puntual distante (como una estrella ) no se enfoca toda en el mismo punto. En particular, la luz que incide en la parte interior del espejo se enfoca más lejos del espejo que la luz que incide en la parte exterior. Como resultado, la imagen no se puede enfocar con tanta nitidez como si la aberración no estuviera presente. Debido a la aberración esférica, los telescopios con una relación focal inferior af /10Generalmente se fabrican con espejos no esféricos o con lentes correctoras.
La aberración esférica se puede eliminar fabricando lentes con una superficie asférica. Descartes demostró que las lentes cuyas superficies son óvalos cartesianos bien elegidos (girados alrededor del eje de simetría central) pueden reflejar perfectamente la luz desde un punto del eje o desde el infinito en la dirección del eje. Un diseño de este tipo permite enfocar la luz de una fuente distante sin ninguna aberración. [2]
En 2018, Rafael G. González-Acuña y Héctor A. Chaparro-Romo, estudiantes de posgrado de la Universidad Nacional Autónoma de México y del Instituto Tecnológico y de Estudios Superiores de Monterrey en México, encontraron una fórmula cerrada para una superficie de lente que elimina la aberración esférica. [3] [4] [5] Su ecuación se puede aplicar para especificar una forma para una superficie de una lente, donde la otra superficie tiene cualquier forma dada.
Muchas de las formas de estimar el diámetro del punto enfocado debido a la aberración esférica se basan en la óptica de rayos. Sin embargo, la óptica de rayos no considera que la luz es una onda electromagnética. Por lo tanto, los resultados pueden ser erróneos debido a los efectos de interferencia que surgen de la naturaleza ondulatoria de la luz.
Un formalismo bastante simple basado en la óptica de rayos, que se aplica solo a lentes delgadas, es la notación de Coddington. [6] En lo que sigue, n es el índice de refracción de la lente, o es la distancia del objeto, i es la distancia de la imagen, h es la distancia desde el eje óptico en el que el rayo más externo ingresa a la lente, es el primer radio de la lente, es el segundo radio de la lente y f es la distancia focal de la lente. La distancia h puede entenderse como la mitad de la apertura libre.
Utilizando los factores de Coddington para la forma, s , y la posición, p ,
La aberración esférica longitudinal se puede escribir como [6]
Si la longitud focal f es mucho mayor que la aberración esférica longitudinal LSA, entonces la aberración esférica transversal, TSA, que corresponde al diámetro del punto focal, viene dada por