La poda alfa-beta es un algoritmo de búsqueda que busca disminuir la cantidad de nodos que son evaluados por el algoritmo minimax en su árbol de búsqueda . Es un algoritmo de búsqueda adversarial que se usa comúnmente para juegos combinatorios de dos jugadores ( tres en raya , ajedrez , Conecta 4 , etc.) con máquinas. Deja de evaluar un movimiento cuando se ha encontrado al menos una posibilidad que demuestra que el movimiento es peor que un movimiento examinado previamente. No es necesario evaluar más estos movimientos. Cuando se aplica a un árbol minimax estándar, devuelve el mismo movimiento que obtendría minimax, pero poda las ramas que no pueden influir en la decisión final. [1]
John McCarthy, durante el taller de Dartmouth, conoció a Alex Bernstein de IBM , que estaba escribiendo un programa de ajedrez. McCarthy inventó la búsqueda alfa-beta y se la recomendó, pero Bernstein no estaba "convencido". [2]
Allen Newell y Herbert A. Simon, que utilizaron lo que John McCarthy llama una "aproximación" [3] en 1958, escribieron que alfa-beta "parece haber sido reinventado varias veces". [4] Arthur Samuel tenía una versión temprana para una simulación de damas. Richards, Timothy Hart, Michael Levin y/o Daniel Edwards también inventaron alfa-beta de forma independiente en los Estados Unidos . [5] McCarthy propuso ideas similares durante el taller de Dartmouth en 1956 y se las sugirió a un grupo de sus estudiantes, incluido Alan Kotok en el MIT en 1961. [6] Alexander Brudno concibió de forma independiente el algoritmo alfa-beta y publicó sus resultados en 1963. [7] Donald Knuth y Ronald W. Moore refinaron el algoritmo en 1975. [8] [9] Judea Pearl demostró su optimalidad en términos del tiempo de ejecución esperado para árboles con valores de hojas asignados aleatoriamente en dos artículos. [10] [11] La optimalidad de la versión aleatoria de alfa-beta fue demostrada por Michael Saks y Avi Wigderson en 1986. [12]
Un árbol de juegos puede representar muchos juegos de suma cero para dos jugadores , como ajedrez, damas y reversi. Cada nodo del árbol representa una posible situación en el juego. A cada nodo terminal (resultado) de una rama se le asigna una puntuación numérica que determina el valor del resultado para el jugador con el siguiente movimiento. [13]
El algoritmo mantiene dos valores, alfa y beta, que representan respectivamente la puntuación mínima que se le asegura al jugador que maximiza y la puntuación máxima que se le asegura al jugador que minimiza. Inicialmente, alfa es infinito negativo y beta es infinito positivo, es decir, ambos jugadores comienzan con su peor puntuación posible. Siempre que la puntuación máxima que se le asegura al jugador que minimiza (es decir, el jugador "beta") se vuelva menor que la puntuación mínima que se le asegura al jugador que maximiza (es decir, el jugador "alfa") (es decir, beta < alfa), el jugador que maximiza no necesita considerar más descendientes de este nodo, ya que nunca se alcanzarán en el juego real.
Para ilustrar esto con un ejemplo de la vida real, supongamos que alguien está jugando al ajedrez y es su turno. La jugada "A" mejorará la posición del jugador. El jugador continúa buscando movimientos para asegurarse de que no se haya olvidado de uno mejor. La jugada "B" también es una buena jugada, pero el jugador se da cuenta de que permitirá al oponente forzar el jaque mate en dos movimientos. Por lo tanto, ya no es necesario considerar otros resultados de la jugada B, ya que el oponente puede forzar una victoria. La puntuación máxima que el oponente podría forzar después de la jugada "B" es menos infinito: una pérdida para el jugador. Esto es menor que la posición mínima que se encontró anteriormente; la jugada "A" no resulta en una pérdida forzada en dos movimientos.

El beneficio de la poda alfa-beta radica en el hecho de que se pueden eliminar ramas del árbol de búsqueda. [13] De esta manera, el tiempo de búsqueda se puede limitar al subárbol "más prometedor" y se puede realizar una búsqueda más profunda en el mismo tiempo. Al igual que su predecesor, pertenece a la clase de algoritmos de ramificación y acotación . La optimización reduce la profundidad efectiva a un poco más de la mitad de la del minimax simple si los nodos se evalúan en un orden óptimo o casi óptimo (la mejor opción para el movimiento lateral ordenado primero en cada nodo).
Con un factor de ramificación (promedio o constante) de b , y una profundidad de búsqueda de d plies , el número máximo de posiciones de nodos de hoja evaluadas (cuando el orden de movimientos es pésimo) es O ( b d ) – lo mismo que una búsqueda minimax simple. Si el orden de movimientos para la búsqueda es óptimo (lo que significa que los mejores movimientos siempre se buscan primero), el número de posiciones de nodos de hoja evaluadas es aproximadamente O ( b ×1× b ×1×...× b ) para profundidad impar y O ( b ×1× b ×1×...×1) para profundidad par, o . En el último caso, donde el ply de una búsqueda es par, el factor de ramificación efectivo se reduce a su raíz cuadrada o, equivalentemente, la búsqueda puede llegar al doble de profundidad con la misma cantidad de cálculo. [14] La explicación de b ×1× b ×1×... es que todos los movimientos del primer jugador deben estudiarse para encontrar el mejor, pero para cada uno, solo se necesita el mejor movimiento del segundo jugador para refutar todos menos el primero (y mejor) movimiento del primer jugador; alfa-beta asegura que no sea necesario considerar ningún otro movimiento del segundo jugador. Cuando los nodos se consideran en un orden aleatorio (es decir, el algoritmo aleatoriza), asintóticamente, el número esperado de nodos evaluados en árboles uniformes con valores de hoja binarios es . [12] Para los mismos árboles, cuando los valores se asignan a los valores de hoja independientemente unos de otros y digamos que cero y uno son igualmente probables, el número esperado de nodos evaluados es , que es mucho menor que el trabajo realizado por el algoritmo aleatorizado, mencionado anteriormente, y nuevamente es óptimo para tales árboles aleatorios. [10] Cuando los valores de hoja se eligen independientemente unos de otros pero del intervalo uniformemente al azar, el número esperado de nodos evaluados aumenta a en el límite, [11] que nuevamente es óptimo para este tipo de árboles aleatorios. Tenga en cuenta que el trabajo real para valores "pequeños" de se aproxima mejor utilizando . [11] [10]
Un programa de ajedrez que busca cuatro capas con un promedio de 36 ramas por nodo evalúa más de un millón de nodos terminales. Una poda alfa-beta óptima eliminaría todos los nodos terminales, excepto unos 2000, una reducción del 99,8 %. [13]
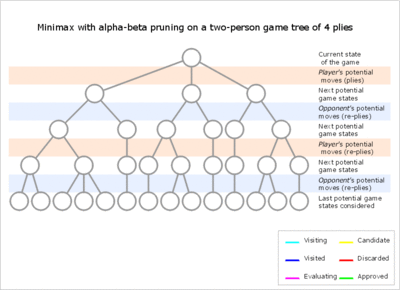
Normalmente, durante la fase alfa-beta, los subárboles están dominados temporalmente por una ventaja del primer jugador (cuando muchos movimientos del primer jugador son buenos y en cada profundidad de búsqueda el primer movimiento verificado por el primer jugador es adecuado, pero se requieren todas las respuestas del segundo jugador para intentar encontrar una refutación), o viceversa. Esta ventaja puede cambiar de bando muchas veces durante la búsqueda si el orden de los movimientos es incorrecto, lo que cada vez genera ineficiencia. Como el número de posiciones buscadas disminuye exponencialmente con cada movimiento más cercano a la posición actual, vale la pena dedicar un esfuerzo considerable a ordenar los movimientos iniciales. Una ordenación mejorada a cualquier profundidad reducirá exponencialmente el número total de posiciones buscadas, pero ordenar todas las posiciones en profundidades cercanas al nodo raíz es relativamente barato ya que hay muy pocas. En la práctica, el orden de los movimientos a menudo se determina por los resultados de búsquedas anteriores más pequeñas, como mediante profundización iterativa .
Además, este algoritmo se puede modificar de forma trivial para devolver una variación principal completa además de la puntuación. Algunos algoritmos más agresivos, como MTD(f), no permiten fácilmente dicha modificación.
El pseudocódigo para el minimax de profundidad limitada con poda alfa-beta es el siguiente: [15]
Las implementaciones de poda alfa-beta a menudo se pueden delinear en función de si son "fail-soft" o "fail-hard". Con la alfa-beta fail-soft, la función alphabeta puede devolver valores (v) que excedan (v < α o v > β) los límites α y β establecidos por sus argumentos de llamada de función. En comparación, la alfa-beta fail-hard limita el valor de retorno de su función dentro del rango inclusivo de α y β. La principal diferencia entre las implementaciones fail-soft y fail-hard es si α y β se actualizan antes o después de la verificación de corte. Si se actualizan antes de la verificación, pueden exceder los límites iniciales y el algoritmo es fail-soft.
El siguiente pseudocódigo ilustra la variación de falla difícil. [15]
función alphabeta(nodo, profundidad, α, β, maximizingPlayer) es si profundidad == 0 o el nodo es terminal entonces devuelve el valor heurístico del nodo si maximizingPlayer entonces valor := −∞ Para cada hijo del nodo hacer valor := máx(valor, alphabeta(hijo, profundidad − 1, α, β, FALSO)) si valor > β entonces se rompe (* β corte *) α := máx(α, valor) valor de retorno de lo contrario valor := +∞ Para cada hijo del nodo hacer valor := min(valor, alphabeta(hijo, profundidad − 1, α, β, VERDADERO)) si valor < α entonces se rompe (* α corte *) β := min(β, valor) valor de retorno
(*Llamada inicial*) alphabeta(origen, profundidad, − ∞ , + ∞ , VERDADERO)
El siguiente pseudocódigo ilustra el algoritmo alpha-beta fail-soft.
función alphabeta(nodo, profundidad, α, β, maximizingPlayer) es si profundidad == 0 o el nodo es terminal entonces devuelve el valor heurístico del nodo si maximizingPlayer entonces valor := −∞ Para cada hijo del nodo hacer valor := máx(valor, alphabeta(hijo, profundidad − 1, α, β, FALSO)) α := máx(α, valor) si valor ≥ β entonces se rompe (* β corte *) devuelve valor de lo contrario valor := +∞ Para cada hijo del nodo hacer valor := min(valor, alphabeta(hijo, profundidad − 1, α, β, VERDADERO)) β := min(β, valor) si valor ≤ α entonces se rompe (* α corte *) valor de retorno
(*Llamada inicial*) alphabeta(origen, profundidad, − ∞ , + ∞ , VERDADERO)
Se pueden lograr mejoras adicionales sin sacrificar la precisión mediante el uso de heurísticas de ordenamiento para buscar partes anteriores del árbol que probablemente fuercen cortes alfa-beta. Por ejemplo, en ajedrez, los movimientos que capturan piezas pueden examinarse antes que los movimientos que no lo hacen, y los movimientos que han obtenido una puntuación alta en pasadas anteriores a través del análisis del árbol de juego pueden evaluarse antes que otros. Otra heurística común y muy barata es la heurística asesina , donde el último movimiento que causó un corte beta en el mismo nivel de árbol en la búsqueda de árboles siempre se examina primero. Esta idea también se puede generalizar en un conjunto de tablas de refutación .
La búsqueda alfa-beta puede hacerse incluso más rápida considerando solo una ventana de búsqueda estrecha (generalmente determinada por conjeturas basadas en la experiencia). Esto se conoce como ventana de aspiración . En el caso extremo, la búsqueda se realiza con alfa y beta iguales; una técnica conocida como búsqueda de ventana cero , búsqueda de ventana nula o búsqueda de explorador . Esto es particularmente útil para búsquedas de victorias/derrotas cerca del final de un juego donde la profundidad adicional obtenida de la ventana estrecha y una función de evaluación de victorias/derrotas simple puede llevar a un resultado concluyente. Si una búsqueda de aspiración falla, es sencillo detectar si falló alto (el borde superior de la ventana era demasiado bajo) o bajo (el borde inferior de la ventana era demasiado alto). Esto brinda información sobre qué valores de ventana podrían ser útiles en una nueva búsqueda de la posición.
Con el tiempo, se han sugerido otras mejoras y, de hecho, la idea de Falphabeta (fail-soft alpha–beta) de John Fishburn es casi universal y ya se ha incorporado anteriormente en una forma ligeramente modificada. Fishburn también sugirió una combinación de la heurística asesina y la búsqueda de ventana cero bajo el nombre de Lalphabeta ("último movimiento con búsqueda alfa–beta de ventana mínima").
Dado que el algoritmo minimax y sus variantes son inherentemente de profundidad primero , una estrategia como la profundización iterativa se utiliza generalmente junto con alfa-beta para que se pueda devolver un movimiento razonablemente bueno incluso si el algoritmo se interrumpe antes de que haya terminado su ejecución. Otra ventaja de utilizar la profundización iterativa es que las búsquedas a profundidades menores dan pistas sobre el orden de los movimientos, así como estimaciones alfa y beta menores, que pueden ayudar a producir puntos de corte para búsquedas de mayor profundidad mucho antes de lo que sería posible de otro modo.
Por otro lado, algoritmos como SSS* utilizan la estrategia del mejor primero . Esto puede hacerlos potencialmente más eficientes en términos de tiempo, pero generalmente a un alto costo en términos de eficiencia de espacio. [16]
Al igual que su contraparte A* para juegos de un solo jugador, SSS* es óptimo en términos de la cantidad promedio de nodos examinados; pero su poder de poda superior se ve más que compensado por el importante espacio de almacenamiento y contabilidad requeridos.