
Los acertijos de vertido de agua (también llamados problemas de jarras de agua , problemas de decantación , [1] [2] acertijos de medición o acertijos de Duro de matar con la venganza ) son una clase de acertijos que involucran una colección finita de jarras de agua de capacidades enteras conocidas (en términos de una medida de líquido como litros o galones ). Inicialmente, cada jarra contiene un volumen entero conocido de líquido, no necesariamente igual a su capacidad.
Los acertijos de este tipo preguntan cuántos pasos de vertido de agua de una jarra a otra (hasta que una jarra se vacíe o la otra se llene) son necesarios para alcanzar un estado objetivo, especificado en términos del volumen de líquido que debe estar presente en alguna jarra o jarras. [3]
Por la identidad de Bézout , tales rompecabezas tienen solución si y sólo si el volumen deseado es un múltiplo del máximo común divisor de todas las capacidades de volumen entero de las jarras.
En estos acertijos se suele suponer que las jarras tienen forma irregular y no están marcadas, por lo que es imposible medir con precisión la cantidad de agua que no llena por completo una jarra. Otras suposiciones de estos problemas pueden incluir que no se puede derramar agua y que cada paso que vierte agua de una jarra de origen a una de destino se detiene cuando la jarra de origen está vacía o la de destino está llena, lo que ocurra primero.
El rompecabezas estándar de este tipo funciona con tres jarras de capacidad 8, 5 y 3 litros. Estas se llenan inicialmente con 8, 0 y 0 litros. En el estado final, deben llenarse con 4, 4 y 0 litros. El rompecabezas se puede resolver en siete pasos, pasando por la siguiente secuencia de estados (indicados como un triple entre corchetes de los tres volúmenes de agua en las tres jarras):
Cowley (1926) escribe que este rompecabezas en particular "se remonta a la época medieval" y señala su aparición en el libro de texto de matemáticas del siglo XVII de Bachet .
Dado que las reglas sólo permiten detenerse/girar en los límites de la cuadrícula cartesiana (es decir, en la capacidad máxima de cada jarra), las únicas acciones reversibles (reversibles en un paso) son:
Las únicas acciones irreversibles que no se pueden revertir en un solo paso son:
Si nos limitamos a las acciones reversibles, podemos construir la solución del problema a partir del resultado deseado. A partir del punto [4,4,0], sólo hay dos acciones reversibles: transferir 3 litros de la jarra de 8 litros a la jarra vacía de 3 litros [1,4,3], y transferir 3 litros de la jarra de 5 litros a la jarra vacía de 3 litros [4,1,3]. Por lo tanto, sólo hay dos soluciones a este problema:

Las reglas a veces se formulan añadiendo un grifo (una "jarra" de agua infinita) y un fregadero (una "jarra" de desagüe que acepta cualquier cantidad de agua sin límite). Llenar una jarra hasta el borde con el grifo o verter todo el contenido de la jarra en el desagüe cuenta como un paso al resolver el problema. Esta versión del rompecabezas apareció en una escena de la película de 1995 Duro de matar 3: la venganza . [4] Esta variante tiene una solución óptima que se puede obtener utilizando un gráfico baricéntrico en forma de billar (o un billar matemático). [5]
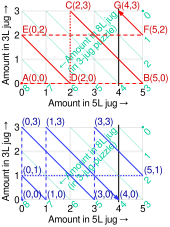
La gráfica muestra dos formas de obtener 4 litros utilizando jarras de 3 y 5 litros, y una fuente de agua y un lavabo en una cuadrícula cartesiana con líneas diagonales de pendiente −1 (de modo que en estas líneas diagonales, que representan el vertido de agua de una jarra a la otra jarra). Los ejes x e y representan las cantidades en las jarras de 5 y 3 L, respectivamente. Partiendo de (0, 0), recorremos la cuadrícula a lo largo de los segmentos de línea, girando solo en sus límites, hasta llegar a la línea negra que denota 4 L en la jarra de 5 L. Las líneas sólidas denotan el vertido entre jarras, las líneas discontinuas denotan el llenado de una jarra y las líneas punteadas denotan el vaciado de una jarra.
Al concatenar cualquiera de las soluciones, el recorrido de la línea de 4 L y el inverso de la otra solución regresa a (0, 0), lo que produce un gráfico de ciclo . Si y solo si los volúmenes de las jarras son coprimos , se visita cada punto límite, lo que da un algoritmo para medir cualquier cantidad entera hasta la suma de los volúmenes.
Como se ha mostrado en la sección anterior, podemos construir la solución del problema a partir del resultado deseado utilizando únicamente acciones reversibles (vaciar una jarra llena en el fregadero y llenar una jarra vacía con el grifo son ambas reversibles). Para obtener 4 litros utilizando jarras de 3 y 5 litros, queremos llegar al punto (4, 0). Desde el punto (4, 0), sólo hay dos acciones reversibles: llenar la jarra vacía de 3 litros hasta llenarla con el grifo (4,3), o transferir 1 litro de agua de la jarra de 5 litros a la de 3 litros (1,3). Por tanto, sólo hay dos soluciones al problema:
El gráfico del ciclo se puede representar mediante los pares ordenados conectados por acciones reversibles:
que contiene todos los estados posibles a los que se puede llegar con una jarra de 3 litros y una de 5 litros. El estado (1, 2), por ejemplo, es imposible de alcanzar desde un estado inicial de (0, 0), ya que (1, 2) tiene ambas jarras parcialmente llenas y no es posible ninguna acción reversible desde este estado.
_Problem_in_Cartesian_coordinates.jpg/440px-Decanting_(water_jugs)_Problem_in_Cartesian_coordinates.jpg)
Otra variante [6] es cuando una de las jarras tiene un volumen conocido de agua para empezar; en ese caso, los volúmenes alcanzables son o bien un múltiplo del máximo común divisor entre los dos recipientes a partir del volumen conocido existente, o bien a partir de cero. Por ejemplo, si una jarra que contiene 8 litros está vacía y la otra jarra que contiene 12 litros tiene 9 litros de agua para empezar, entonces con una fuente (grifo) y un desagüe (fregadero), estas dos jarras pueden medir volúmenes de 9 litros, 5 litros, 1 litro, así como 12 litros, 8 litros, 4 litros y 0 litros. La solución más simple para 5 litros es (9,0) → (9,8) → (12,5); la solución más simple para 4 litros es (9,0) → (12,0) → (4,8). Estas soluciones se pueden visualizar mediante flechas rojas y azules en una cuadrícula cartesiana con líneas diagonales (de pendiente -1 tal que en estas líneas diagonales) espaciadas 4 litros entre sí, tanto horizontal como verticalmente.
De nuevo, si nos limitamos a las acciones reversibles, a partir del punto buscado (5,0), sólo hay dos acciones reversibles: trasvasar 5 litros de agua de la jarra de 12 litros a la de 8 litros (0,5), o llenar la jarra de 8 litros vacía hasta llenarla con agua del grifo (5,8). Por tanto, sólo hay dos soluciones al problema:
Para la pregunta de los 4 litros, como , es necesaria una acción irreversible al comienzo de la solución; podría ser simplemente verter los 9 litros de agua de la jarra de 12 litros en el fregadero (0,0), o llenarla completamente hasta los 12 litros del grifo (12,0). Luego, podemos construir nuestras soluciones al revés como antes:

Si el número de jarras es tres, el estado de llenado después de cada paso se puede describir en un diagrama de coordenadas baricéntricas , porque la suma de los tres números enteros permanece igual a lo largo de todos los pasos. [7] En consecuencia, los pasos se pueden visualizar como movimientos de billar en el sistema de coordenadas (recortado) en una red triangular.
El gráfico baricéntrico de la derecha ofrece dos soluciones para los acertijos de 8, 5 y 3 L. El área amarilla indica las combinaciones que se pueden lograr con las jarras. A partir del cuadrado, los caminos de color rojo sólido y azul discontinuo muestran las transiciones que se pueden verter. Cuando un vértice cae sobre el triángulo negro punteado, se han medido 4 L. Otro vertido al rombo arroja 4 L en cada una de las jarras de 8 y 5 L.
El camino azul es un paso más corto que el camino del puzzle de las dos jarras con grifo y desagüe, ya que podemos acumular 4 L en la jarra de 8 L, ausente en la variante de dos jarras.