Vecino más cercano de gran margen

Algoritmo estadístico de aprendizaje automático para el aprendizaje métrico.

La clasificación del vecino más cercano de margen grande ( LMNN ) ^[1] es un algoritmo estadístico de aprendizaje automático para el aprendizaje métrico . Aprende una pseudométrica diseñada para la clasificación de k vecinos más cercanos . El algoritmo se basa en programación semidefinida , una subclase de optimización convexa .

El objetivo del aprendizaje supervisado (más específicamente la clasificación) es aprender una regla de decisión que pueda categorizar instancias de datos en clases predefinidas. La regla del vecino k-más cercano supone un conjunto de datos de entrenamiento de instancias etiquetadas (es decir, las clases son conocidas). Clasifica una nueva instancia de datos con la clase obtenida del voto mayoritario de las k instancias de entrenamiento más cercanas (etiquetadas). La cercanía se mide con una métrica predefinida . Los vecinos más cercanos de margen grande son un algoritmo que aprende esta (pseudo)métrica global de forma supervisada para mejorar la precisión de la clasificación de la regla del vecino k-más cercano.

Configuración

La principal intuición detrás de LMNN es aprender una pseudométrica según la cual todas las instancias de datos en el conjunto de entrenamiento están rodeadas por al menos k instancias que comparten la misma etiqueta de clase. Si esto se logra, se minimiza el error de dejar uno fuera (un caso especial de validación cruzada ). Deje que los datos de entrenamiento consistan en un conjunto de datos , donde está el conjunto de posibles categorías de clases . ${\displaystyle D=\{({\vec {x}}_{1},y_{1}),\dots ,({\vec {x}}_{n},y_{n})\}\subset R^{d}\times C}$ ${\displaystyle C=\{1,\dots ,c\}}$

El algoritmo aprende una pseudométrica del tipo

${\displaystyle d({\vec {x}}_{i},{\vec {x}}_{j})=({\vec {x}}_{i}-{\vec {x}}_{j})^{\top }\mathbf {M} ({\vec {x}}_{i}-{\vec {x}}_{j})}$.

Para que esté bien definida, la matriz debe ser semidefinida positiva . La métrica euclidiana es un caso especial, donde está la matriz identidad. Esta generalización a menudo se denomina (falsamente ^{[ cita requerida ] )} métrica de Mahalanobis . ${\displaystyle d(\cdot ,\cdot )}$ ${\displaystyle \mathbf {M} }$ ${\displaystyle \mathbf {M} }$

La Figura 1 ilustra el efecto de la métrica bajo variaciones . Los dos círculos muestran el conjunto de puntos con igual distancia al centro . En el caso euclidiano este conjunto es un círculo, mientras que bajo la métrica modificada (Mahalanobis) se convierte en un elipsoide . ${\displaystyle \mathbf {M} }$ ${\displaystyle {\vec {x}}_{i}}$

Figura 1: Ilustración esquemática de LMNN.

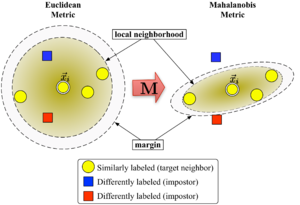
El algoritmo distingue entre dos tipos de puntos de datos especiales: vecinos objetivo e impostores .

Vecinos objetivo

Los vecinos objetivo se seleccionan antes de aprender. Cada instancia tiene vecinos objetivo exactamente diferentes , los cuales comparten la misma etiqueta de clase . Los vecinos objetivo son los puntos de datos que deberían convertirse en vecinos más cercanos según la métrica aprendida . Denotaremos el conjunto de vecinos objetivo para un punto de datos como . ${\displaystyle {\vec {x}}_{i}}$ ${\displaystyle k}$ ${\displaystyle D}$ ${\displaystyle y_{i}}$ ${\displaystyle {\vec {x}}_{i}}$ ${\displaystyle N_{i}}$

Impostores

Un impostor de un punto de datos es otro punto de datos con una etiqueta de clase diferente (es decir , ) que es uno de los vecinos más cercanos de . Durante el aprendizaje, el algoritmo intenta minimizar la cantidad de impostores para todas las instancias de datos en el conjunto de entrenamiento. ${\displaystyle {\vec {x}}_{i}}$ ${\displaystyle {\vec {x}}_{j}}$ ${\displaystyle y_{i}\neq y_{j}}$ ${\displaystyle {\vec {x}}_{i}}$

Algoritmo

Los vecinos más cercanos de gran margen optimizan la matriz con la ayuda de la programación semidefinida . El objetivo es doble: para cada punto de datos , los vecinos objetivo deben estar cerca y los impostores deben estar lejos . La Figura 1 muestra el efecto de dicha optimización en un ejemplo ilustrativo. La métrica aprendida hace que el vector de entrada esté rodeado por instancias de entrenamiento de la misma clase. Si fuera un punto de prueba, se clasificaría correctamente según la regla del vecino más cercano. ${\displaystyle \mathbf {M} }$ ${\displaystyle {\vec {x}}_{i}}$ ${\displaystyle {\vec {x}}_{i}}$ ${\displaystyle k=3}$

El primer objetivo de optimización se logra minimizando la distancia promedio entre las instancias y sus vecinos objetivo.

${\displaystyle \sum _{i,j\in N_{i}}d({\vec {x}}_{i},{\vec {x}}_{j})}$.

El segundo objetivo se logra penalizando las distancias a los impostores que están a menos de una unidad de distancia de los vecinos objetivo (y, por lo tanto, expulsándolos del vecindario local de ). El valor resultante a minimizar se puede expresar como: ${\displaystyle {\vec {x}}_{l}}$ ${\displaystyle {\vec {x}}_{j}}$ ${\displaystyle {\vec {x}}_{i}}$

${\displaystyle \sum _{i,j\in N_{i},l,y_{l}\neq y_{i}}[d({\vec {x}}_{i},{\vec {x}}_{j})+1-d({\vec {x}}_{i},{\vec {x}}_{l})]_{+}}$

Con función de pérdida de bisagra , que garantiza que la proximidad del impostor no sea penalizada cuando esté fuera del margen. El margen de exactamente una unidad fija la escala de la matriz . Cualquier elección alternativa daría como resultado un cambio de escala de por un factor de . ${\textstyle [\cdot ]_{+}=\max(\cdot ,0)}$ ${\displaystyle M}$ ${\displaystyle c>0}$ ${\displaystyle M}$ ${\displaystyle 1/c}$

El problema de optimización final se convierte en:

${\displaystyle \min _{\mathbf {M} }\sum _{i,j\in N_{i}}d({\vec {x}}_{i},{\vec {x}}_{j})+\lambda \sum _{i,j,l}\xi _{ijl}}$

${\displaystyle \forall _{i,j\in N_{i},l,y_{l}\neq y_{i}}}$

${\displaystyle d({\vec {x}}_{i},{\vec {x}}_{j})+1-d({\vec {x}}_{i},{\vec {x}}_{l})\leq \xi _{ijl}}$

${\displaystyle \xi _{ijl}\geq 0}$

${\displaystyle \mathbf {M} \succeq 0}$

El hiperparámetro es una constante positiva (normalmente establecida mediante validación cruzada). Aquí las variables (junto con dos tipos de restricciones) reemplazan el término en la función de costos. Desempeñan un papel similar al de las variables de holgura para absorber el alcance de las violaciones de las restricciones del impostor. La última restricción asegura que sea semidefinida positiva. El problema de optimización es un ejemplo de programación semidefinida (SDP). Aunque los SDP tienden a sufrir una alta complejidad computacional, esta instancia de SDP en particular se puede resolver de manera muy eficiente debido a las propiedades geométricas subyacentes del problema. En particular, la mayoría de las restricciones del impostor se satisfacen naturalmente y no es necesario aplicarlas durante el tiempo de ejecución (es decir, el conjunto de variables es escaso). Una técnica de resolución particularmente adecuada es el método del conjunto de trabajo , que mantiene un pequeño conjunto de restricciones que se aplican activamente y monitorea las restricciones restantes (probablemente satisfechas) sólo ocasionalmente para garantizar su corrección. ${\textstyle \lambda >0}$ ${\displaystyle \xi _{ijl}}$ ${\displaystyle \mathbf {M} }$ ${\displaystyle \xi _{ijl}}$

Extensiones y solucionadores eficientes

LMNN se amplió a múltiples métricas locales en el documento de 2008. ^[2] Esta extensión mejora significativamente el error de clasificación, pero implica un problema de optimización más costoso. En su publicación de 2009 en el Journal of Machine Learning Research, ^[3] Weinberger y Saul obtienen un solucionador eficiente para el programa semidefinido. Puede aprender una métrica para el conjunto de datos de dígitos escritos a mano MNIST en varias horas, lo que implica miles de millones de restricciones por pares. Una implementación de Matlab de código abierto está disponible gratuitamente en la página web del autor.

Kumal et al. ^[4] amplió el algoritmo para incorporar invarianzas locales a transformaciones polinómicas multivariadas y mejoró la regularización.

Ver también

• Aprendizaje por similitud
• Análisis discriminante lineal
• Aprendizaje de la cuantificación de vectores
• Espacio pseudométrico
• Búsqueda de vecino más cercano
• Análisis de conglomerados
• Clasificación de datos
• Procesamiento de datos
• Aprendizaje automático
• Reconocimiento de patrones
• Análisis predictivo
• Reducción de dimensiones
• Análisis de componentes del barrio.

Referencias

1. Weinberger, KQ; BlitzerJC; Saúl LK (2006). "Aprendizaje métrico a distancia para la clasificación del vecino más cercano de gran margen". Avances en los sistemas de procesamiento de información neuronal . 18 : 1473-1480.
2. Weinberger, KQ; Saúl LK (2008). "Solucionadores rápidos e implementaciones eficientes para el aprendizaje métrico a distancia" (PDF) . Actas de la conferencia internacional sobre aprendizaje automático : 1160–1167. Archivado desde el original (PDF) el 24 de julio de 2011 . Consultado el 14 de julio de 2010 .
3. Weinberger, KQ; Saúl LK (2009). "Aprendizaje métrico a distancia para clasificación de grandes márgenes" (PDF) . Revista de investigación sobre aprendizaje automático . 10 : 207–244.
4. Kumar, diputado; Torr PHS; Zisserman A. (2007). "Un clasificador de vecino más cercano invariante de gran margen". 2007 IEEE 11ª Conferencia Internacional sobre Visión por Computadora . págs. 1–8. doi :10.1109/ICCV.2007.4409041. ISBN 978-1-4244-1630-1. S2CID  1326101.

enlaces externos

• Implementación de Matlab
• Tutorial ICML 2010 sobre aprendizaje de métricas