El principio de autoconsistencia de Novikov , también conocido como conjetura de autoconsistencia de Novikov y ley de conservación de la historia de Larry Niven , es un principio desarrollado por el físico ruso Ígor Dmitrievich Novikov a mediados de la década de 1980. Novikov pretendía resolver el problema de las paradojas en los viajes en el tiempo , lo que teóricamente está permitido en ciertas soluciones de la relatividad general que contienen lo que se conoce como curvas temporales cerradas . El principio afirma que si existe un evento que causaría una paradoja o cualquier "cambio" en el pasado, entonces la probabilidad de ese evento es cero. Por lo tanto, sería imposible crear paradojas temporales .
Los físicos saben desde hace tiempo que algunas soluciones a la teoría de la relatividad general contienen curvas temporales cerradas , como por ejemplo la métrica de Gödel . Novikov analizó la posibilidad de las curvas temporales cerradas (CTC) en libros que escribió en 1975 y 1983 [1] , y opinó que solo se permitirían viajes autoconsistentes en el tiempo. [2] En un artículo de 1990 de Novikov y otros, " El problema de Cauchy en los espacio-tiempos con curvas temporales cerradas", [3] los autores afirman:
El único tipo de violación de la causalidad que los autores considerarían inaceptable es el que se materializa en el concepto de ciencia ficción de retroceder en el tiempo y matar al yo más joven ("cambiar el pasado"). Hace algunos años, uno de nosotros (Novikov) consideró brevemente la posibilidad de que pudieran existir las CTC y argumentó que no pueden implicar este tipo de violación de la causalidad: los eventos en una CTC ya están garantizados como autoconsistentes, argumentó Novikov; se influyen entre sí alrededor de una curva cerrada de una manera autoajustada, cíclica y autoconsistente. Los otros autores han llegado recientemente al mismo punto de vista.
Incorporaremos este punto de vista en un principio de autoconsistencia, que establece que las únicas soluciones a las leyes de la física que pueden darse localmente en el Universo real son aquellas que son globalmente autoconsistentes. Este principio permite construir una solución local a las ecuaciones de la física sólo si esa solución local puede extenderse a una parte de una solución global (no necesariamente única), que está bien definida en todas las regiones no singulares del espacio-tiempo.
Entre los coautores de este artículo de 1990 se encontraban Kip Thorne , Mike Morris y Ulvi Yurtsever, quienes en 1988 habían despertado un renovado interés en el tema de los viajes en el tiempo en la relatividad general con su artículo "Agujeros de gusano, máquinas del tiempo y la condición de energía débil", [4] que mostraba que una nueva solución de la relatividad general conocida como agujero de gusano atravesable podía conducir a curvas temporales cerradas y, a diferencia de las soluciones anteriores que contenían CTC, no requería condiciones poco realistas para el universo en su conjunto. Después de discusiones con el autor principal del artículo de 1990, John Friedman, se convencieron de que los viajes en el tiempo no tenían por qué conducir a paradojas irresolubles, independientemente del objeto enviado a través del agujero de gusano. [5] : 509

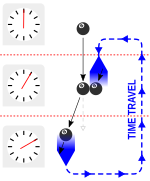
Como respuesta, el físico Joseph Polchinski les escribió una carta en la que argumentaba que se podría evitar la cuestión del libre albedrío empleando un experimento mental potencialmente paradójico que implicaba enviar una bola de billar al pasado a través de un agujero de gusano. En el escenario de Polchinski, la bola de billar se lanza al agujero de gusano en un ángulo tal que, si continúa su camino, saldrá en el pasado en el ángulo justo para colisionar con su yo anterior, sacándola de su trayectoria e impidiéndole entrar en el agujero de gusano en primer lugar. Thorne se referiría a este escenario como " la paradoja de Polchinski " en 1994. [6] : 510–511
Tras considerar el escenario, Fernando Echeverría y Gunnar Klinkhammer, dos estudiantes de Caltech (donde enseñaba Thorne), llegaron a una solución al problema que presenta los mismos elementos que la solución que Feynman y Wheeler [7] denominaron la solución del "golpe oblicuo", para evitar las inconsistencias que surgen de los bucles de causalidad. En el escenario revisado, la pelota del futuro emerge en un ángulo diferente al que genera la paradoja y le da a su yo más joven un golpe oblicuo en lugar de golpearlo completamente fuera del agujero de gusano. Este golpe altera su trayectoria en el grado justo, lo que significa que viajará hacia atrás en el tiempo con el ángulo requerido para darle a su yo más joven el golpe oblicuo necesario. Echeverría y Klinkhammer descubrieron que había más de una solución autoconsistente, con ángulos ligeramente diferentes para el golpe oblicuo en cada situación. Un análisis posterior de Thorne y Robert Forward ilustró que, para ciertas trayectorias iniciales de la bola de billar, en realidad podría haber un número infinito de soluciones autoconsistentes. [6] : 511–513
Echeverría, Klinkhammer y Thorne publicaron un artículo en el que discutían estos resultados en 1991; [8] además, informaron que habían tratado de ver si podían encontrar alguna condición inicial para la bola de billar para la cual no hubiera extensiones autoconsistentes, pero no pudieron hacerlo. Por lo tanto, es plausible que existan extensiones autoconsistentes para cada trayectoria inicial posible, aunque esto no se ha demostrado. [9] : 184 Esto solo se aplica a las condiciones iniciales fuera de la región del espacio-tiempo que viola la cronología, [9] : 187 que está limitada por un horizonte de Cauchy . [10] Esto podría significar que el principio de autoconsistencia de Novikov en realidad no impone ninguna restricción a los sistemas fuera de la región del espacio-tiempo donde es posible viajar en el tiempo, solo dentro de ella.
Incluso si se pueden encontrar extensiones autoconsistentes para condiciones iniciales arbitrarias fuera del horizonte de Cauchy, el hallazgo de que puede haber múltiples extensiones autoconsistentes distintas para la misma condición inicial (de hecho, Echeverría et al. encontraron un número infinito de extensiones consistentes para cada trayectoria inicial que analizaron [9] : 184 ) puede verse como problemático, ya que clásicamente no parece haber forma de decidir qué extensión elegirán las leyes de la física. Para superar esta dificultad, Thorne y Klinkhammer analizaron el escenario de la bola de billar utilizando la mecánica cuántica, [6] : 514–515 realizando una suma mecánico-cuántica sobre historias ( integral de trayectoria ) utilizando solo las extensiones consistentes, y encontraron que esto resultó en una probabilidad bien definida para cada extensión consistente. Los autores de "Cauchy problem in spacetimes with closed timelike curves" escriben:
La forma más sencilla de imponer el principio de autoconsistencia en la mecánica cuántica (en un espacio-tiempo clásico) es mediante una formulación de suma sobre historias en la que se incluyen todas aquellas, y sólo aquellas, historias que son autoconsistentes. Resulta que, al menos formalmente (módulo cuestiones como la convergencia de la suma), para cada elección de la función de onda inicial no relativista de la bola de billar antes del horizonte de Cauchy , dicha suma sobre historias produce probabilidades únicas y autoconsistentes para los resultados de todos los conjuntos de mediciones posteriores. ... Sospechamos, de forma más general, que para cualquier sistema cuántico en un espacio-tiempo clásico de agujero de gusano con un horizonte de Cauchy estable, la suma sobre todas las historias autoconsistentes dará probabilidades únicas y autoconsistentes para los resultados de todos los conjuntos de mediciones que uno podría elegir hacer.
El principio de consistencia de Novikov presupone ciertas condiciones sobre qué tipo de viaje en el tiempo es posible. En concreto, presupone que solo existe una línea temporal o que no es posible acceder a líneas temporales alternativas (como las postuladas por la interpretación de los múltiples mundos de la mecánica cuántica ).
Teniendo en cuenta estos supuestos, la restricción de que el viaje en el tiempo no debe conducir a resultados inconsistentes podría verse simplemente como una tautología , una verdad evidente que no puede ser falsa. Sin embargo, el principio de autoconsistencia de Novikov pretende ir más allá de la simple afirmación de que la historia debe ser consistente, haciendo la suposición adicional no trivial de que el universo obedece las mismas leyes locales de la física en situaciones que implican viajes en el tiempo que en regiones del espacio-tiempo que carecen de curvas temporales cerradas. Esto se aclara en el "problema de Cauchy en espacio-tiempos con curvas temporales cerradas" mencionado anteriormente, [3] donde los autores escriben:
Que el principio de autoconsistencia no es totalmente tautológico se hace evidente cuando se considera la siguiente alternativa: las leyes de la física podrían permitir las CTC; y cuando ocurren, podrían desencadenar nuevos tipos de física local que no hemos conocido anteriormente. ... El principio de autoconsistencia tiene por objeto descartar ese comportamiento. Insiste en que la física local está gobernada por los mismos tipos de leyes físicas que manejamos en ausencia de CTC: las leyes que implican un valor único autoconsistente para los campos. En esencia, el principio de autoconsistencia es un principio de que no hay nueva física. Si uno se inclina desde el principio a ignorar o descartar la posibilidad de nueva física, entonces considerará la autoconsistencia como un principio trivial.
Las hipótesis del principio de autoconsistencia pueden extenderse a escenarios hipotéticos que involucran viajeros inteligentes en el tiempo, así como objetos no inteligentes como bolas de billar. Los autores de "Cauchy problem in spacetimes with closed timelike curves " comentaron sobre el tema en la conclusión del artículo, escribiendo:
Si se permiten las CTC y si la visión anterior de la adaptación de la física teórica a ellas resulta ser más o menos correcta, ¿qué implicará esto sobre la noción filosófica del libre albedrío para los humanos y otros seres inteligentes? Sin duda implicará que los seres inteligentes no pueden cambiar el pasado. Tal cambio es incompatible con el principio de autoconsistencia. En consecuencia, cualquier ser que atravesara un agujero de gusano e intentara cambiar el pasado se vería impedido por la ley física de realizar el cambio; es decir, el "libre albedrío" del ser estaría limitado. Aunque esta restricción tiene un carácter más global que las restricciones al libre albedrío que se desprenden de las leyes estándar y locales de la física, no es obvio para nosotros que esta restricción sea más severa que las impuestas por la ley física estándar. [3]
De manera similar, el físico y astrónomo J. Craig Wheeler concluye que:
Según la conjetura de la consistencia, cualquier interacción interpersonal compleja debe resolverse de manera coherente para que no haya paradojas. Esa es la solución. Esto significa, si se toma literalmente, que si existen máquinas del tiempo, no puede haber libre albedrío. No puedes obligarte a matar a tu yo más joven si viajas al pasado. Puedes coexistir, salir a tomar una cerveza, celebrar tu cumpleaños juntos, pero de alguna manera las circunstancias dictarán que no puedes comportarte de una manera que conduzca a una paradoja en el tiempo. Novikov apoya este punto de vista con otro argumento: la física ya restringe tu libre albedrío todos los días. Puedes obligarte a volar o a atravesar una pared de hormigón, pero la gravedad y la física de la materia condensada dictan que no puedes. ¿Por qué, pregunta Novikov, la restricción de consistencia impuesta a un viajero en el tiempo es diferente? [11]
La lógica de bucle temporal, acuñada por el roboticista y futurista Hans Moravec , [12] es un sistema hipotético de computación que explota el principio de autoconsistencia de Novikov para calcular respuestas mucho más rápido de lo que es posible con el modelo estándar de complejidad computacional utilizando máquinas de Turing . En este sistema, una computadora envía un resultado de un cálculo hacia atrás en el tiempo y se basa en el principio de autoconsistencia para forzar que el resultado enviado sea correcto, siempre que la máquina pueda recibir información confiable del futuro y siempre que el algoritmo y el mecanismo subyacente sean formalmente correctos . Aún se puede producir un resultado incorrecto o ningún resultado si no se garantiza que el mecanismo o algoritmo de viaje en el tiempo sea preciso.
Un ejemplo sencillo es un algoritmo de método iterativo . Moravec afirma:
Construya una máquina de computación que acepte una entrada que represente una solución aproximada a un problema y produzca una salida que sea una aproximación mejorada. Convencionalmente, aplicaría un cálculo de este tipo repetidamente un número finito de veces y luego se conformaría con el resultado mejor, pero aún aproximado. Dado un retraso negativo apropiado, es posible otra cosa: [...] el resultado de cada iteración de la función se devuelve en el tiempo para que sirva como la "primera" aproximación. Tan pronto como se activa la máquina, aparece (¡por una coincidencia extraordinaria!) de manera inmediata y constante un denominado "punto fijo" de F, una entrada que produce una salida idéntica, que generalmente indica una respuesta perfecta. [...] Si la iteración no converge, es decir, si F no tiene un punto fijo, las salidas y entradas de la computadora se apagarán o se mantendrán en un estado intermedio improbable.
El físico David Deutsch demostró en 1991 que este modelo de computación podía resolver problemas NP en tiempo polinomial [13] , y Scott Aaronson luego extendió este resultado para mostrar que el modelo también podía usarse para resolver problemas PSPACE en tiempo polinomial [14] [15] Deutsch muestra que la computación cuántica con un retraso negativo (viaje en el tiempo hacia atrás) produce solo soluciones autoconsistentes, y la región que viola la cronología impone restricciones que no son evidentes a través del razonamiento clásico [13] . Los investigadores publicaron en 2014 una simulación en la que afirman haber validado el modelo de Deutsch con fotones. [16] Sin embargo, en un artículo de Tolksdorf y Verch se demostró que la condición de autoconsistencia de Deutsch puede cumplirse con precisión arbitraria en cualquier sistema cuántico descrito según la teoría cuántica de campos relativista incluso en espaciotiempos que no admiten curvas temporales cerradas, lo que pone en duda si el modelo de Deutsch es realmente característico de los procesos cuánticos que simulan curvas temporales cerradas en el sentido de la relatividad general . [17] En un artículo posterior, [18] los mismos autores muestran que la condición de punto fijo CTC de Deutsch también puede cumplirse en cualquier sistema sujeto a las leyes de la mecánica estadística clásica , incluso si no está construido por sistemas cuánticos. Los autores concluyen que, por tanto, la condición de Deutsch no es específica de la física cuántica, ni depende de la naturaleza cuántica de un sistema físico para que pueda cumplirse. En consecuencia, Tolksdorf y Verch argumentan que la condición de Deutsch no es lo suficientemente específica como para permitir afirmaciones sobre escenarios de viaje en el tiempo o su realización hipotética por la física cuántica.
Posteriormente, Seth Lloyd [19] [20] presentó una propuesta alternativa basada en la postselección y las integrales de trayectoria. En particular, la integral de trayectoria se aplica a cuerpos de un solo valor, lo que conduce a historias autoconsistentes.
La paradoja de Polchinski.