En lógica matemática , un término denota un objeto matemático , mientras que una fórmula denota un hecho matemático. En particular, los términos aparecen como componentes de una fórmula. Esto es análogo al lenguaje natural, donde una frase nominal se refiere a un objeto y una oración completa se refiere a un hecho.
Un término de primer orden se construye recursivamente a partir de símbolos constantes, variables y símbolos de función . Una expresión formada al aplicar un símbolo de predicado a un número apropiado de términos se llama fórmula atómica , que evalúa como verdadera o falsa en lógicas bivalentes , dada una interpretación . Por ejemplo, es un término construido a partir de la constante 1, la variable x y los símbolos de función binaria y ; es parte de la fórmula atómica que evalúa como verdadera para cada valor de número real de x .
Además de en lógica , los términos juegan papeles importantes en el álgebra universal y en los sistemas de reescritura .
Dado un conjunto V de símbolos variables, un conjunto C de símbolos constantes y conjuntos F n de símbolos de funciones n -arias, también llamados símbolos de operador, para cada número natural n ≥ 1, el conjunto de términos (de primer orden no ordenados) T se define recursivamente como el conjunto más pequeño con las siguientes propiedades: [1]
Usando una notación pseudogramatical intuitiva , esto a veces se escribe así:
La firma del término lenguaje describe qué conjuntos de símbolos de función F n están habitados. Ejemplos bien conocidos son los símbolos de función unaria sen , cos ∈ F 1 , y los símbolos de función binaria +, −, ⋅, / ∈ F 2 . Las operaciones ternarias y las funciones de aridad superior son posibles pero poco comunes en la práctica. Muchos autores consideran los símbolos constantes como símbolos de función 0-arios F 0 , por lo que no necesitan una clase sintáctica especial para ellos.
Un término denota un objeto matemático del dominio del discurso . Una constante c denota un objeto nombrado de ese dominio, una variable x abarca los objetos de ese dominio y una función n -aria f asigna n - tuplas de objetos a objetos. Por ejemplo, si n ∈ V es un símbolo de variable, 1 ∈ C es un símbolo de constante y add ∈ F 2 es un símbolo de función binaria, entonces n ∈ T , 1 ∈ T y (por lo tanto) add ( n , 1) ∈ T por la primera, segunda y tercera regla de construcción de términos, respectivamente. El último término se escribe generalmente como n +1, utilizando la notación infija y el símbolo de operador más común + para mayor comodidad.
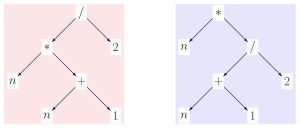
Originalmente, los lógicos definían un término como una cadena de caracteres que se ajustaba a ciertas reglas de construcción. [2] Sin embargo, desde que el concepto de árbol se hizo popular en la ciencia informática, resultó más conveniente pensar en un término como un árbol. Por ejemplo, varias cadenas de caracteres distintas, como " ( n ⋅( n +1))/2 ", " (( n ⋅( n +1)))/2 " y " ", denotan el mismo término y corresponden al mismo árbol, es decir, el árbol de la izquierda en la imagen anterior. Al separar la estructura de árbol de un término de su representación gráfica en papel, también es fácil tener en cuenta los paréntesis (que son solo representación, no estructura) y los operadores de multiplicación invisibles (que existen solo en la estructura, no en la representación).
Se dice que dos términos son estructuralmente , literalmente o sintácticamente iguales si corresponden al mismo árbol. Por ejemplo, el árbol izquierdo y el derecho en la imagen anterior son términos estructuralmente desiguales , aunque podrían considerarse " semánticamente iguales " ya que siempre evalúan el mismo valor en aritmética racional . Mientras que la igualdad estructural se puede comprobar sin ningún conocimiento sobre el significado de los símbolos, la igualdad semántica no. Si la función / se interpreta, por ejemplo, no como racional sino como división de enteros truncados , entonces en n = 2 el término izquierdo y el derecho evalúan a 3 y 2, respectivamente. Los términos estructuralmente iguales deben coincidir en sus nombres de variable.
Por el contrario, un término t se denomina un cambio de nombre , o una variante , de un término u si este último resultó de cambiar sistemáticamente el nombre de todas las variables del primero, es decir, si u = tσ para alguna sustitución de cambio de nombre σ. En ese caso, u también es un cambio de nombre de t , ya que una sustitución de cambio de nombre σ tiene una inversa σ −1 y t = uσ −1 . Se dice entonces que ambos términos son iguales módulo cambio de nombre . En muchos contextos, los nombres de las variables particulares de un término no importan, p. ej., el axioma de conmutatividad para la adición se puede enunciar como x + y = y + x o como a + b = b + a ; en tales casos, se puede cambiar el nombre de toda la fórmula, mientras que un subtérmino arbitrario normalmente no, p. ej., x + y = b + a no es una versión válida del axioma de conmutatividad. [nota 1] [nota 2]
El conjunto de variables de un término t se denota por vars ( t ). Un término que no contiene ninguna variable se denomina término fundamental ; un término que no contiene múltiples ocurrencias de una variable se denomina término lineal . Por ejemplo, 2+2 es un término fundamental y, por lo tanto, también un término lineal, x ⋅( n +1) es un término lineal, n ⋅( n +1) es un término no lineal. Estas propiedades son importantes, por ejemplo, en la reescritura de términos .
Dada una signatura para los símbolos de función, el conjunto de todos los términos forma el álgebra de términos libre . El conjunto de todos los términos básicos forma el álgebra de términos inicial .
Abreviando el número de constantes como f 0 , y el número de símbolos de funciones i -arias como f i , el número θ h de términos fundamentales distintos de una altura hasta h se puede calcular mediante la siguiente fórmula de recursión:
Dado un conjunto R n de símbolos de relación n -arios para cada número natural n ≥ 1, se obtiene una fórmula atómica (de primer orden no ordenada) aplicando un símbolo de relación n -ario a n términos. En cuanto a los símbolos de función, un conjunto de símbolos de relación R n normalmente no está vacío solo para n pequeños. En lógica matemática, las fórmulas más complejas se construyen a partir de fórmulas atómicas utilizando conectivos lógicos y cuantificadores . Por ejemplo, dejando denotar el conjunto de números reales , ∀ x : x ∈ ⇒ ( x +1)⋅( x +1) ≥ 0 es una fórmula matemática que se evalúa como verdadera en el álgebra de números complejos . Una fórmula atómica se llama fundamental si se construye completamente a partir de términos fundamentales; todas las fórmulas atómicas fundamentales componibles a partir de un conjunto dado de símbolos de función y predicado conforman la base de Herbrand para estos conjuntos de símbolos.

Cuando el dominio del discurso contiene elementos de tipos básicamente diferentes, es útil dividir el conjunto de todos los términos en consecuencia. Para este fin, se asigna una clasificación (a veces también llamada tipo ) a cada variable y a cada símbolo de constante, y una declaración [nota 3] de clasificaciones de dominio y clasificación de rango a cada símbolo de función. Un término clasificado f ( t 1 ,..., t n ) puede estar compuesto de subtérminos clasificados t 1 ,..., t n solo si la clasificación del i ésimo subtérmino coincide con la i ésima clasificación de dominio declarada de f . Un término de este tipo también se denomina bien clasificado ; cualquier otro término (es decir, que solo obedezca las reglas de no clasificación) se denomina mal clasificado .
Por ejemplo, un espacio vectorial viene con un campo asociado de números escalares. Sean W y N los tipos de vectores y números, respectivamente, sean V W y V N el conjunto de variables vectoriales y numéricas, respectivamente, y C W y C N el conjunto de constantes vectoriales y numéricas, respectivamente. Entonces, eg y 0 ∈ C N , y la suma vectorial, la multiplicación escalar y el producto interno se declaran como , y , respectivamente. Suponiendo símbolos de variable y a , b ∈ V N , el término está bien ordenado, mientras que no lo está (ya que + no acepta un término de tipo N como segundo argumento). Para hacer un término bien ordenado, se requiere una declaración adicional . Los símbolos de función que tienen varias declaraciones se denominan sobrecargados .
Consulte la lógica multiordenada para obtener más información, incluidas las extensiones del marco multiordenado que se describe aquí.
Las notaciones matemáticas que se muestran en la tabla no encajan en el esquema de un término de primer orden como se definió anteriormente, ya que todas introducen una variable local o ligada propia que puede no aparecer fuera del alcance de la notación, p. ej. no tiene sentido. Por el contrario, las otras variables, denominadas libres , se comportan como variables de término de primer orden ordinarias, p. ej. tiene sentido.
Todos estos operadores pueden considerarse como si tomaran una función en lugar de un término de valor como uno de sus argumentos. Por ejemplo, el operador lim se aplica a una secuencia, es decir, a una asignación de un entero positivo a, por ejemplo, números reales. Como otro ejemplo, una función C para implementar el segundo ejemplo de la tabla, Σ, tendría un argumento de puntero de función (ver el cuadro a continuación).
Los términos lambda se pueden utilizar para denotar funciones anónimas que se proporcionarán como argumentos a lim , Σ, ∫, etc.
Por ejemplo, la función cuadrado del programa C a continuación se puede escribir anónimamente como un término lambda λ i . i 2 . El operador suma general Σ puede entonces considerarse como un símbolo de función ternaria que toma un valor de límite inferior, un valor de límite superior y una función a sumar. Debido a su último argumento, el operador Σ se llama símbolo de función de segundo orden . Como otro ejemplo, el término lambda λ n . x / n denota una función que mapea 1, 2, 3, ... a x /1, x /2, x /3, ..., respectivamente, es decir, denota la secuencia ( x /1, x /2, x /3, ...). El operador lim toma dicha secuencia y devuelve su límite (si está definido).
La columna más a la derecha de la tabla indica cómo cada ejemplo de notación matemática puede representarse mediante un término lambda, convirtiendo también los operadores infijos comunes en forma de prefijo .
int suma ( int lwb , int upb , int fct ( int )) { // implementa el operador de suma general int res = 0 ; for ( int i = lwb ; i <= upb ; ++ i ) res += fct ( i ); return res ; } int square ( int i ) { return i * i ; } // implementa una función anónima (lambda i. i*i); sin embargo, C requiere un nombre para ella #include <stdio.h> int main ( void ) { int n ; scanf ( " %d" , & n ); printf ( "%d \n " , sum ( 1 , n , square )); // aplica el operador suma para sumar los cuadrados return 0 ; } Dado un conjunto V de símbolos variables, el conjunto de términos lambda se define recursivamente de la siguiente manera:
Los ejemplos motivadores anteriores también utilizan algunas constantes como div , power , etc., que, sin embargo, no se admiten en el cálculo lambda puro.
Intuitivamente, la abstracción λ x . t denota una función unaria que devuelve t cuando se da x , mientras que la aplicación ( t 1 t 2 ) denota el resultado de llamar a la función t 1 con la entrada t 2 . Por ejemplo, la abstracción λ x . x denota la función identidad, mientras que λ x . y denota la función constante que siempre devuelve y . El término lambda λ x .( x x ) toma una función x y devuelve el resultado de aplicar x a sí misma.