dispersión caótica

La dispersión caótica es una rama de la teoría del caos que se ocupa de los sistemas de dispersión que muestran una fuerte sensibilidad a las condiciones iniciales . En un sistema de dispersión clásico habrá uno o más parámetros de impacto , b , en los que se envía una partícula al dispersor. Esto da lugar a uno o más parámetros de salida, y , cuando la partícula sale hacia el infinito. Mientras la partícula atraviesa el sistema, también puede haber un tiempo de retraso , T (el tiempo que tarda la partícula en salir del sistema), además de la distancia recorrida, s . En ciertos sistemas (por ejemplo, sistemas "tipo billar" en los que la partícula sufre colisiones sin pérdidas con objetos duros y fijos), los dos serán equivalentes (ver más abajo). En un sistema de dispersión caótico, un cambio mínimo en el parámetro de impacto puede dar lugar a un cambio muy grande en los parámetros de salida.

Sistema Gaspard-Arroz

Fig. 1: Diagrama del sistema de dispersión Gaspard-Rice que muestra los principales parámetros.

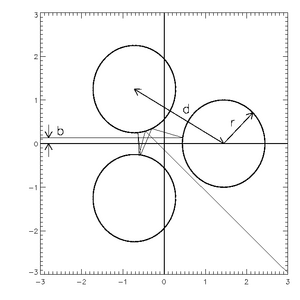
Un excelente ejemplo de sistema es el sistema de dispersión "Gaspard-Rice" (GR) ^[1] , también conocido simplemente como sistema de "tres discos", que incorpora muchos de los conceptos importantes de la dispersión caótica y al mismo tiempo es simple y fácil de entender y simular. El concepto es muy simple: tenemos tres discos duros dispuestos en una formación triangular, se envía una partícula puntual y sufre colisiones elásticas perfectas hasta que sale hacia el infinito. En esta discusión, solo consideraremos sistemas GR que tengan discos del mismo tamaño, igualmente espaciados alrededor de los puntos de un triángulo equilátero.

La Figura 1 ilustra este sistema, mientras que la Figura 2 muestra dos trayectorias de ejemplo. Tenga en cuenta primero que las trayectorias rebotan alrededor del sistema durante algún tiempo antes de salir finalmente. Tenga en cuenta también que si consideramos que los parámetros del impacto son el inicio de las dos líneas perfectamente horizontales de la izquierda (el sistema es completamente reversible: el punto de salida también podría ser el punto de entrada), las dos trayectorias están inicialmente tan cerca como para ser casi idéntico. Cuando salen, son completamente diferentes, lo que ilustra la fuerte sensibilidad a las condiciones iniciales. Este sistema se utilizará como ejemplo a lo largo del artículo.

Fig. 2: Sistema de dispersión Gaspard-Rice que muestra sensibilidad a las condiciones iniciales.

Tasa de descomposición

Si introducimos una gran cantidad de partículas con parámetros de impacto uniformemente distribuidos, la velocidad a la que salen del sistema se conoce como tasa de desintegración. Podemos calcular la tasa de caída simulando el sistema durante muchas pruebas y formando un histograma del tiempo de retraso , T. Para el sistema GR, es fácil ver que el tiempo de retraso y la longitud de la trayectoria de la partícula son equivalentes excepto por un coeficiente de multiplicación. Una elección típica para el parámetro de impacto es la coordenada y , mientras que el ángulo de la trayectoria se mantiene constante en cero grados (horizontal). Mientras tanto, decimos que la partícula ha "salido del sistema" una vez que pasa una frontera a una distancia arbitraria, pero suficientemente grande, del centro del sistema.

Esperamos que el número de partículas que quedan en el sistema, N(T) , varíe como:

${\displaystyle N(T)\sim e^{-\gamma T}}$

Por tanto, la tasa de desintegración , , viene dada como: ${\displaystyle \gamma }$

${\displaystyle \gamma =\lim _{n\rightarrow \infty }-{\frac {\ln N(T)}{T}}}$

donde n es el número total de partículas. ^[2]

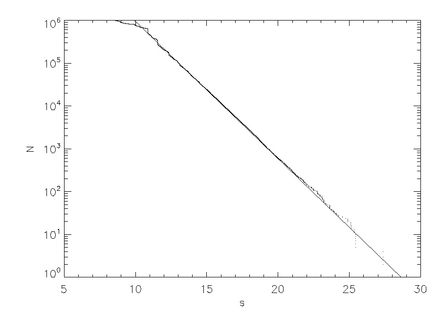
La Figura 3 muestra una gráfica de la longitud del camino versus el número de partículas para una simulación de un millón (1e6) de partículas iniciadas con el parámetro de impacto aleatorio, b . Se superpone una recta ajustada de pendiente negativa . La longitud del camino, s , es equivalente al tiempo de caída, T , siempre que escalemos la velocidad (constante) de manera adecuada. Tenga en cuenta que una tasa de caída exponencial es una propiedad específica de la dispersión caótica hiperbólica. Los dispersores no hiperbólicos pueden tener una tasa de caída aritmética. ^[3] ${\displaystyle \gamma =0.739}$

Fig. 3: Tasa de descomposición del sistema de dispersión Gaspard-Rice.

Un sistema experimental y la variedad estable.

Fig. 4: Un sistema de dispersión experimental de Gaspard-Rice. ^[4]

La Figura 4 muestra una realización experimental del sistema Gaspard-Rice utilizando un láser en lugar de una partícula puntual. Como sabe cualquiera que haya probado esto, este no es un método muy eficaz para probar el sistema: el rayo láser se dispersa en todas direcciones. Como lo muestran Sweet, Ott y Yorke, ^[5] un método más eficaz es dirigir luz de colores a través de los espacios entre los discos (o en este caso, pegar tiras de papel de colores entre pares de cilindros) y ver los reflejos a través de un espejo abierto. brecha. El resultado es un patrón complejo de rayas de colores alternos, como se muestra a continuación, que se ve más claramente en la versión simulada a continuación.

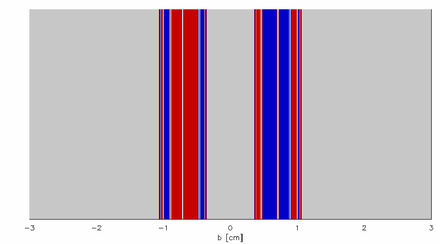
Las figuras 5 y 6 muestran las cuencas de atracción para cada parámetro de impacto, b , es decir, para un valor dado de b , ¿por qué espacio sale la partícula? Los límites de las cuencas forman un conjunto de Cantor y representan miembros de la variedad estable : trayectorias que, una vez iniciadas, nunca salen del sistema.

Fig. 5: Un sistema de dispersión experimental de Gaspard-Rice que muestra cuencas de atracción. ^[4]

Fig 6: Simulación del sistema de dispersión Gaspard-Rice que muestra cuencas de atracción. ^[4]

El conjunto invariante y la dinámica simbólica

Fig. 7: Posibles variables para representar el sistema Gaspard-Rice como un mapa de funciones iteradas. ^[6]

Mientras sea simétrico, podemos pensar fácilmente en el sistema como un mapa de funciones iteradas , un método común para representar un sistema dinámico y caótico. ^[7] La ​​Figura 7 muestra una posible representación de las variables, con la primera variable, representando el ángulo alrededor del disco en el rebote y la segunda, representando el ángulo de impacto/rebote con respecto al disco. Un subconjunto de estas dos variables, llamado conjunto invariante, se asignará a sí mismo. Este conjunto, cuyos cuatro miembros se muestran en las Figuras 8 y 9, será fractal , totalmente no atractivo y de medida cero. Esta es una inversión interesante de los sistemas caóticos más comúnmente discutidos en los que el conjunto invariante fractal atrae y de hecho comprende la(s) cuenca(s) de atracción. Tenga en cuenta que la naturaleza totalmente no atractiva del conjunto invariante es otra propiedad de un dispersor caótico hiperbólico. ${\displaystyle \theta \in [-\pi ,\pi ]}$ ${\displaystyle \phi \in [-\pi /2,\pi /2]}$

Fig. 8: Cuatro miembros del conjunto invariante del sistema Gaspard-Rice.

Fig. 9: Cuatro miembros del conjunto invariante del sistema Gaspard-Rice, iterados hacia adelante en el tiempo.

Cada miembro del conjunto invariante se puede modelar mediante dinámica simbólica : la trayectoria se etiqueta en función de cada uno de los discos en los que rebota. El conjunto de todas esas secuencias forma un conjunto incontable . ^[8] Para los cuatro miembros mostrados en las Figuras 8 y 9, la dinámica simbólica será la siguiente: ^[3]

...121212121212......232323232323......313131313131......123123123123...

Los miembros de la variedad estable también pueden representarse, excepto que cada secuencia tendrá un punto de partida. Cuando se considera que un miembro del conjunto invariante debe "encajar" en los límites entre dos cuencas de atracción, es evidente que, si se perturba, la trayectoria puede salir en cualquier punto de la secuencia. Por lo tanto, también debería ser evidente que existirá un número infinito de cuencas alternas de los tres "colores" entre cualquier límite dado. ^{[2] [3] [8]}

Debido a su naturaleza inestable, es difícil acceder directamente a los miembros del conjunto invariante o de la variedad estable. El exponente de incertidumbre está idealmente diseñado para medir la dimensión fractal de este tipo de sistema. Una vez más, utilizando el parámetro de impacto único, b , realizamos múltiples pruebas con parámetros de impacto aleatorios, perturbándolos en una cantidad mínima, y ​​contando con qué frecuencia cambia el número de rebotes de los discos, es decir, la fracción de incertidumbre. Tenga en cuenta que aunque el sistema es bidimensional, un solo parámetro de impacto es suficiente para medir la dimensión fractal de la variedad estable. Esto se demuestra en la Figura 10, que muestra las cuencas de atracción trazadas en función de un parámetro de impacto dual, y . La variedad estable, que se puede ver en los límites entre las cuencas, es fractal en una sola dimensión. ${\displaystyle \epsilon }$ ${\displaystyle \theta }$ ${\displaystyle \phi }$

Fig. 10: Las cuencas de atracción en función de los parámetros de impacto dual, y . ^[6] ${\displaystyle \theta }$ ${\displaystyle \phi }$

La Figura 11 representa la fracción de incertidumbre, f , en función de la incertidumbre, para un sistema Gaspard-Rice simulado. La pendiente de la curva ajustada devuelve el exponente de incertidumbre, por lo que la dimensión de conteo de cajas de la variedad estable es ,. El conjunto invariante es la intersección de las variedades estable e inestable . ^[9] ${\displaystyle \epsilon }$ ${\displaystyle \gamma =0.380}$ ${\displaystyle D_{0}=N-\gamma =2-0.380=1.62}$

Dado que el sistema es el mismo ya sea que se ejecute hacia adelante o hacia atrás, la variedad inestable es simplemente la imagen especular de la variedad estable y sus dimensiones fractales serán iguales. ^[8] Sobre esta base podemos calcular la dimensión fractal del conjunto invariante: ^[2]

${\displaystyle D=D_{s}+D_{u}-N=2D_{s}-N=N-2\gamma }$

donde D_s y D_u son las dimensiones fractales de las variedades estable e inestable, respectivamente y N =2 es la dimensionalidad del sistema. La dimensión fractal del conjunto invariante es D =1,24.

Fig. 10: Gráfico de la fracción de incertidumbre del sistema de dispersión de Gaspard-Rice, con ajuste en línea recta, que da un exponente de incertidumbre .

Relación entre la dimensión fractal, la tasa de desintegración y los exponentes de Lyapunov

De la discusión anterior, debería resultar evidente que la tasa de desintegración, la dimensión fractal y los exponentes de Lyapunov están todos relacionados. El gran exponente de Lyapunov, por ejemplo, nos dice qué tan rápido divergirá una trayectoria en el conjunto invariante si se perturba. De manera similar, la dimensión fractal nos dará información sobre la densidad de órbitas en el conjunto invariante. Por lo tanto, podemos ver que ambos afectarán la tasa de desintegración como se refleja en la siguiente conjetura para un sistema de dispersión bidimensional: ^[2]

${\displaystyle D_{1}=\left(h_{1}-{\frac {1}{\gamma }}\right)\left({\frac {1}{h_{1}}}-{\frac {1}{h_{2}}}\right)}$

donde D ₁ es la dimensión de información y h ₁ y h ₂ son los exponentes de Lyapunov pequeño y grande, respectivamente. Para un atractor, se reduce a la conjetura de Kaplan-Yorke . ^[2] ${\displaystyle \gamma =\infty }$

Ver también

• Lagos de Wada
• Exponente de incertidumbre

Referencias

1. Gaspard, Pedro; Arroz, Stuart A. (15 de febrero de 1989). "Dispersión de un repelente clásicamente caótico". La Revista de Física Química . 90 (4). Publicación AIP: 2225–2241. doi : 10.1063/1.456017. ISSN  0021-9606.
2. Edward Ott (1993). Caos en sistemas dinámicos . Prensa de la Universidad de Cambridge .
3. Yalçinkaya, Tolga; Lai, Ying-Cheng (1995). "Dispersión caótica". Computadoras en Física . 9 (5). Publicación AIP: 511–518. doi : 10.1063/1.168549 . ISSN  0894-1866.
4. Peter Mills (2000). Se investiga un sistema experimental de dispersión caótica clásica (informe técnico). Universidad de Waterloo.
5. David Sweet, Edward Ott y James A. Yorke. "Topología compleja en dispersión caótica: una observación de laboratorio". Naturaleza . 399 : 313.
6. Peter Mills (1998). Dispersión caótica ruidosa (Tesis). Universidad de Waterloo.
7. Denny Gulick (1992). Encuentros con el Caos . McGraw-Hill .
8. Bleher, Siegfried; Grebogi, Celso ; Ott, Eduardo (1990). "Bifurcación a dispersión caótica". Physica D: Fenómenos no lineales . 46 (1). Elsevier BV: 87-121. doi :10.1016/0167-2789(90)90114-5. ISSN  0167-2789.
9. Ott, Eduardo; Tél, Tamás (1993). "Dispersión caótica: una introducción" (PDF) . Caos: una revista interdisciplinaria de ciencia no lineal . 3 (4). Publicación AIP: 417–426. doi : 10.1063/1.165949. ISSN  1054-1500. PMID  12780049.

enlaces externos

• Software para simular el sistema Gaspard-Rice
• Una simulación del sistema Gaspard-Rice y su dinámica simbólica, de Chaos V: Duhem's Bull