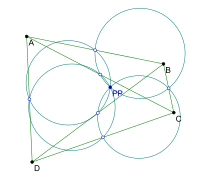
En geometría , el punto Poncelet de cuatro puntos dados se define de la siguiente manera:
Sean A, B, C, D cuatro puntos en el plano que no forman un sistema ortocéntrico y tales que no hay tres de ellos colineales . Los círculos de nueve puntos de los triángulos △ ABC , △ BCD , △ CDA , △ DAB se encuentran en un punto, el punto Poncelet de los puntos A, B, C, D . (Si A, B, C, D forman un sistema ortocéntrico, entonces los triángulos △ ABC , △ BCD , △ CDA , △ DAB comparten el mismo círculo de nueve puntos, y el punto Poncelet no está definido.)
Si A, B, C, D no están en un círculo, el punto Poncelet de A, B, C, D está en el círculo circunscrito del triángulo pedal de D con respecto al triángulo △ ABC y está en los otros círculos análogos. (Si están en un círculo, entonces esos triángulos pedal serán líneas; a saber, la línea de Simson de D con respecto al triángulo △ ABC y las otras líneas de Simson análogas. En ese caso, esas líneas aún concurren en el punto Poncelet, que también será el anticentro del cuadrilátero cíclico cuyos vértices son A, B, C, D ).
El punto Poncelet de A, B, C, D se encuentra en el círculo a través de la intersección de las líneas AB y CD , la intersección de las líneas AC y BD , y la intersección de las líneas AD y BC (asumiendo que existen todas estas intersecciones).
El punto Poncelet de A, B, C, D es el centro de la única hipérbola rectangular que pasa por A, B, C, D.