Prismatoide

Poliedro con todos los vértices en dos planos paralelos

Prismatoide con caras paralelas A ₁ y A ₃ , sección transversal intermedia A ₂ y altura h

En geometría , un prismatoide es un poliedro cuyos vértices se encuentran todos en dos planos paralelos . Sus caras laterales pueden ser trapecios o triángulos . ^[1] Si ambos planos tienen el mismo número de vértices y las caras laterales son paralelogramos o trapecios, se denomina prismoide . ^[2]

Volumen

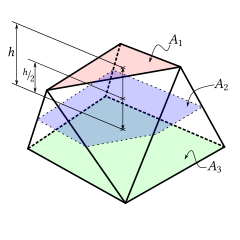
Si las áreas de las dos caras paralelas son A ₁ y A ₃ , el área de la sección transversal de la intersección del prismatoide con un plano intermedio entre las dos caras paralelas es A ₂ , y la altura (la distancia entre las dos caras paralelas) es h , entonces el volumen del prismatoide está dado por ^[3] Esta fórmula se deduce inmediatamente integrando el área paralela a los dos planos de vértices por la regla de Simpson , ya que esa regla es exacta para la integración de polinomios de grado hasta 3, y en este caso el área es como máximo una función cuadrática en la altura. $${\displaystyle V={\frac {h(A_{1}+4A_{2}+A_{3})}{6}}.}$$

Familias prismatoides

Las familias de prismatoides incluyen:

• Pirámides , en las que un plano contiene sólo un punto;
• Cuñas , en las que un plano contiene sólo dos puntos;
• Prismas , cuyos polígonos en cada plano son congruentes y están unidos por rectángulos o paralelogramos;
• Antiprismas , cuyos polígonos en cada plano son congruentes y están unidos por una franja alternada de triángulos;
• Antiprismas estelares ;
• Cúpulas , en las que el polígono en un plano contiene el doble de puntos que el otro y está unido a éste mediante triángulos y rectángulos alternados;
• Frusta obtenida por truncamiento de una pirámide o de un cono;
• Prismatoides hexaédricos de caras cuadriláteras :
  1. Paralelepípedos : seis caras de paralelogramo
  2. Romboedros – seis caras de rombo
  3. Trapezoedros trigonales : seis caras congruentes de un rombo
  4. Cuboides : seis caras rectangulares
  5. Fructo cuadrilátero : pirámide cuadrada truncada con vértice
  6. Cubo – seis caras cuadradas

Dimensiones superiores

Una cúpula tetraédrica-cuboctaédrica.

En general, un politopo es prismático si sus vértices se encuentran en dos hiperplanos . Por ejemplo, en cuatro dimensiones, dos poliedros pueden ubicarse en dos 3-espacios paralelos y conectarse entre sí mediante lados poliédricos.

Referencias

1. Kern, William F.; Bland, James R. (1938). Medición de sólidos con pruebas. pág. 75.
2. Alsina, Claudi; Nelsen, Roger B. (2015). Una odisea espacial matemática: geometría sólida en el siglo XXI. Asociación Matemática de Estados Unidos . pág. 85. ISBN 9780883853580.
3. Meserve, BE; Pingry, RE (1952). "Algunas notas sobre la fórmula prismoidal". El profesor de matemáticas . 45 (4): 257–263. JSTOR  27954012.

Enlaces externos

• Weisstein, Eric W. "Prismatoide". MundoMatemático .