
En geometría , la orientación , actitud , rumbo , dirección o posición angular de un objeto (como una línea , un plano o un cuerpo rígido ) es parte de la descripción de cómo se coloca en el espacio que ocupa. [1] Más específicamente, se refiere a la rotación imaginaria que se necesita para mover el objeto desde una ubicación de referencia a su ubicación actual. Una rotación puede no ser suficiente para alcanzar la ubicación actual, en cuyo caso puede ser necesario agregar una traslación imaginaria para cambiar la posición del objeto (o posición lineal). La posición y la orientación juntas describen completamente cómo se coloca el objeto en el espacio. Se puede pensar que la rotación y la traslación imaginarias mencionadas anteriormente ocurren en cualquier orden, ya que la orientación de un objeto no cambia cuando se traslada y su posición no cambia cuando gira.
El teorema de rotación de Euler muestra que en tres dimensiones se puede alcanzar cualquier orientación con una sola rotación alrededor de un eje fijo . Esto proporciona una forma común de representar la orientación utilizando una representación eje-ángulo . Otros métodos ampliamente utilizados incluyen cuaterniones de rotación , rotores , ángulos de Euler o matrices de rotación . Los usos más especializados incluyen índices de Miller en cristalografía, rumbo y buzamiento en geología y pendiente en mapas y señales. Un vector unitario también se puede utilizar para representar la dirección del vector normal de un objeto o la dirección relativa entre dos puntos.
Normalmente, la orientación se da en relación con un marco de referencia , normalmente especificado por un sistema de coordenadas cartesianas .
En general, la posición y orientación en el espacio de un cuerpo rígido se definen como la posición y orientación, con respecto al marco de referencia principal, de otro marco de referencia, que es fijo con respecto al cuerpo y, por lo tanto, se traslada y rota con él (el marco de referencia local del cuerpo o sistema de coordenadas local ). Se necesitan al menos tres valores independientes para describir la orientación de este marco local. Otros tres valores describen la posición de un punto en el objeto. Todos los puntos del cuerpo cambian su posición durante una rotación, excepto aquellos que se encuentran en el eje de rotación. Si el cuerpo rígido tiene simetría rotacional, no todas las orientaciones son distinguibles, excepto observando cómo evoluciona la orientación en el tiempo a partir de una orientación inicial conocida. Por ejemplo, la orientación en el espacio de una línea , segmento de línea o vector se puede especificar con solo dos valores, por ejemplo, dos cosenos directores . Otro ejemplo es la posición de un punto en la Tierra, a menudo descrita utilizando la orientación de una línea que lo une con el centro de la Tierra, medida utilizando los dos ángulos de longitud y latitud . Del mismo modo, la orientación de un plano también se puede describir con dos valores, por ejemplo, especificando la orientación de una línea normal a ese plano o utilizando los ángulos de rumbo y de inmersión.
En las siguientes secciones se dan más detalles sobre los métodos matemáticos para representar la orientación de cuerpos rígidos y planos en tres dimensiones.
En dos dimensiones, la orientación de cualquier objeto (línea, vector o figura plana ) viene dada por un único valor: el ángulo que ha girado. Sólo hay un grado de libertad y un único punto fijo alrededor del cual se produce la rotación.
Cuando hay d dimensiones, la especificación de una orientación de un objeto que no tiene ninguna simetría rotacional requiere d ( d − 1) / 2 valores independientes.
Se han desarrollado varios métodos para describir las orientaciones de un cuerpo rígido en tres dimensiones, que se resumen en las siguientes secciones.

El primer intento de representar una orientación se atribuye a Leonhard Euler . Imaginó tres sistemas de referencia que pudieran girar uno alrededor del otro, y se dio cuenta de que partiendo de un sistema de referencia fijo y realizando tres rotaciones, podía obtener cualquier otro sistema de referencia en el espacio (utilizando dos rotaciones para fijar el eje vertical y otra para fijar los otros dos ejes). Los valores de estas tres rotaciones se denominan ángulos de Euler .

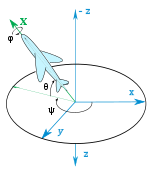
Se trata de tres ángulos, también conocidos como ángulos de guiñada, de cabeceo y de balanceo, ángulos de navegación y ángulos de Cardan. Matemáticamente constituyen un conjunto de seis posibilidades dentro de los doce conjuntos posibles de ángulos de Euler, siendo el ordenamiento el más utilizado para describir la orientación de un vehículo como un avión. En ingeniería aeroespacial se suelen denominar ángulos de Euler.

Euler también se dio cuenta de que la composición de dos rotaciones es equivalente a una sola rotación sobre un eje fijo diferente ( teorema de rotación de Euler ). Por lo tanto, la composición de los tres ángulos anteriores tiene que ser igual a una sola rotación, cuyo eje era complicado de calcular hasta que se desarrollaron las matrices.
Basándose en este hecho, introdujo una forma vectorial de describir cualquier rotación, con un vector en el eje de rotación y módulo igual al valor del ángulo. Por lo tanto, cualquier orientación puede representarse mediante un vector de rotación (también llamado vector de Euler) que conduce a ella desde el sistema de referencia. Cuando se utiliza para representar una orientación, el vector de rotación se denomina comúnmente vector de orientación o vector de actitud.
Un método similar, llamado representación eje-ángulo , describe una rotación u orientación utilizando un vector unitario alineado con el eje de rotación y un valor separado para indicar el ángulo (ver figura).
Con la introducción de las matrices, se reescribieron los teoremas de Euler. Las rotaciones se describieron mediante matrices ortogonales denominadas matrices de rotación o matrices de coseno de dirección. Cuando se utiliza para representar una orientación, una matriz de rotación se denomina comúnmente matriz de orientación o matriz de actitud.
El vector de Euler mencionado anteriormente es el vector propio de una matriz de rotación (una matriz de rotación tiene un único valor propio real ). El producto de dos matrices de rotación es la composición de rotaciones. Por lo tanto, como antes, la orientación se puede dar como la rotación desde el sistema inicial hasta alcanzar el sistema que queremos describir.
El espacio de configuración de un objeto no simétrico en un espacio n -dimensional es SO( n ) × R n . La orientación se puede visualizar uniendo una base de vectores tangentes a un objeto. La dirección en la que apunta cada vector determina su orientación.
Otra forma de describir las rotaciones es mediante cuaterniones de rotación , también llamados versores. Son equivalentes a las matrices de rotación y a los vectores de rotación. Con respecto a los vectores de rotación, se pueden convertir más fácilmente a matrices y viceversa. Cuando se utilizan para representar orientaciones, los cuaterniones de rotación se denominan normalmente cuaterniones de orientación o cuaterniones de actitud.
La actitud de un cuerpo rígido es su orientación, tal como se describe, por ejemplo, mediante la orientación de un marco fijo en el cuerpo con respecto a un marco de referencia fijo. La actitud se describe mediante coordenadas de actitud y consta de al menos tres coordenadas. [2] Un esquema para orientar un cuerpo rígido se basa en la rotación de los ejes del cuerpo; rotaciones sucesivas tres veces sobre los ejes del marco de referencia fijo del cuerpo, estableciendo así los ángulos de Euler del cuerpo . [3] [4] Otro se basa en el balanceo, el cabeceo y la guiñada , [5] aunque estos términos también se refieren a desviaciones incrementales de la actitud nominal.
la actitud de un plano o una línea —es decir, su orientación en el espacio— es fundamental para la descripción de las estructuras.
Actitud de cuerpo rígido según ángulo de Euler.