El origami rígido es una rama del origami que se ocupa de plegar estructuras utilizando láminas rígidas planas unidas por bisagras . Es decir, a diferencia del origami tradicional, los paneles de papel no se pueden doblar durante el proceso de plegado; deben permanecer planos en todo momento y el papel solo se dobla a lo largo de sus bisagras. Un modelo de origami rígido seguiría siendo plegable si estuviera hecho de láminas de vidrio con bisagras en lugar de sus líneas de pliegue.
Sin embargo, no es necesario que la estructura comience como una única lámina plana: por ejemplo, las bolsas de compras con fondos planos se estudian como parte del origami rígido.
El origami rígido es una parte del estudio de las matemáticas del plegado de papel , y las estructuras de origami rígidas pueden considerarse como un tipo de enlace mecánico . El origami rígido tiene una gran utilidad práctica.
El número de bases de origami estándar que se pueden plegar utilizando origami rígido está restringido por sus reglas. [1] El origami rígido no tiene que seguir los axiomas de Huzita-Hatori , las líneas de plegado se pueden calcular en lugar de tener que construirse a partir de líneas y puntos existentes. Al plegar origami rígido en forma plana, el teorema de Kawasaki y el teorema de Maekawa restringen los patrones de plegado que son posibles, tal como lo hacen en el origami convencional, pero ya no forman una caracterización exacta: algunos patrones que se pueden plegar en forma plana en el origami convencional no se pueden plegar en forma plana de manera rígida. [2]
El teorema de Bellows dice que un poliedro flexible tiene volumen constante cuando se flexiona rígidamente. [3]
El problema de doblar la servilleta plantea la cuestión de si es posible doblar un cuadrado de modo que el perímetro de la figura plana resultante aumente. En 2004, AS Tarasov demostró que esto se puede resolver con origami rígido. [4]
El blooming es un movimiento de origami rígido de la red de un poliedro desde su estado desplegado plano hasta el poliedro plegado, o viceversa. Aunque cada poliedro convexo tiene una red con un blooming, no se sabe si existe un blooming que no corte las caras del poliedro, o si todas las redes de poliedros convexos tienen bloomings. [5]
Determinar si todos los pliegues de un patrón de pliegues se pueden doblar simultáneamente como una pieza de origami rígido, o si se puede doblar un subconjunto de los pliegues, son ambos NP-hard . Esto es cierto incluso para determinar la existencia de un movimiento de plegado que mantiene el papel arbitrariamente cerca de su estado plano, por lo que (a diferencia de otros resultados en la dureza del plegado de patrones de pliegues de origami) este resultado no depende de la imposibilidad de autointersecciones del papel doblado. [6]
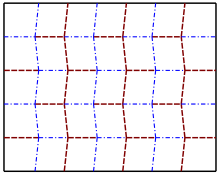
El pliegue Miura es un pliegue rígido que se ha utilizado para embalar grandes conjuntos de paneles solares para satélites espaciales, que deben plegarse antes de su despliegue.
Robert J. Lang ha aplicado el origami rígido al problema de plegar un telescopio espacial. [7]
Aunque las bolsas de papel para la compra suelen doblarse hasta quedar planas y luego desplegarse, el patrón de plegado estándar para hacerlo no es rígido; los lados de la bolsa se doblan ligeramente cuando se dobla y desdobla. La tensión del papel debido a esta flexión hace que se rompa en sus dos estados planos, la bolsa doblada y la abierta. [8]
Martin Gardner ha popularizado los flexágonos , que son una forma de origami rígido, y el flexatubo. [9]
Los caleidociclos son juguetes, generalmente hechos de papel, que al girarlos dan un efecto similar al de un caleidoscopio.
{{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )