La estadística de prueba es una cantidad derivada de la muestra para la prueba de hipótesis estadística . [1] Una prueba de hipótesis se especifica típicamente en términos de una estadística de prueba, considerada como un resumen numérico de un conjunto de datos que reduce los datos a un valor que puede usarse para realizar la prueba de hipótesis. En general, una estadística de prueba se selecciona o define de tal manera que cuantifique, dentro de los datos observados, los comportamientos que distinguirían la hipótesis nula de la hipótesis alternativa , cuando se prescribe dicha alternativa, o que caracterizarían la hipótesis nula si no hay una hipótesis alternativa explícitamente establecida.
Una propiedad importante de una estadística de prueba es que su distribución de muestreo bajo la hipótesis nula debe ser calculable, ya sea de forma exacta o aproximada, lo que permite calcular los valores p . Una estadística de prueba comparte algunas de las mismas cualidades de una estadística descriptiva , y muchas estadísticas se pueden utilizar tanto como estadísticas de prueba como estadísticas descriptivas. Sin embargo, una estadística de prueba está específicamente destinada a su uso en pruebas estadísticas, mientras que la principal cualidad de una estadística descriptiva es que es fácilmente interpretable. Algunas estadísticas descriptivas informativas, como el rango de muestra , no son buenas estadísticas de prueba ya que es difícil determinar su distribución de muestreo.
Dos estadísticas de prueba ampliamente utilizadas son la estadística t y la estadística F.
Supongamos que la tarea consiste en comprobar si una moneda es justa (es decir, si tiene las mismas probabilidades de obtener cara o cruz). Si se lanza la moneda 100 veces y se registran los resultados, los datos brutos se pueden representar como una secuencia de 100 caras y cruces. Si se interesa por la probabilidad marginal de obtener cruz, solo es necesario registrar la cantidad T de los 100 lanzamientos que produjeron cruz. Pero T también se puede utilizar como estadística de prueba de una de dos maneras:
Utilizando una de estas distribuciones de muestreo, es posible calcular un valor p unilateral o bilateral para la hipótesis nula de que la moneda es justa. En este caso, la estadística de prueba reduce un conjunto de 100 números a un único resumen numérico que se puede utilizar para realizar pruebas.
Las pruebas de una muestra son adecuadas cuando se compara una muestra con la población a partir de una hipótesis. Las características de la población se conocen a partir de la teoría o se calculan a partir de la población.
Las pruebas de dos muestras son apropiadas para comparar dos muestras, generalmente muestras experimentales y de control de un experimento controlado científicamente.
Las pruebas pareadas son adecuadas para comparar dos muestras en las que es imposible controlar variables importantes. En lugar de comparar dos conjuntos, los miembros se emparejan entre muestras, de modo que la diferencia entre los miembros se convierte en la muestra. Por lo general, la media de las diferencias se compara con cero. El ejemplo habitual de cuándo es adecuada una prueba de diferencias pareadas es cuando se aplica algo a un único conjunto de sujetos de prueba y la prueba tiene como objetivo comprobar si existe un efecto.
Las pruebas Z son apropiadas para comparar medias en condiciones estrictas con respecto a la normalidad y una desviación estándar conocida.
Una prueba t es apropiada para comparar medias en condiciones relajadas (se supone que son menores).
Las pruebas de proporciones son análogas a las pruebas de medias (la proporción del 50%).
Las pruebas de chi-cuadrado utilizan los mismos cálculos y la misma distribución de probabilidad para diferentes aplicaciones:
Las pruebas F (análisis de varianza, ANOVA) se utilizan habitualmente para decidir si las agrupaciones de datos por categoría son significativas. Si la varianza de las puntuaciones de las pruebas de los zurdos de una clase es mucho menor que la varianza de toda la clase, puede ser útil estudiar a los zurdos como grupo. La hipótesis nula es que dos varianzas son iguales, por lo que la agrupación propuesta no es significativa.
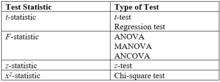
En la siguiente tabla, los símbolos utilizados se definen en la parte inferior de la tabla. Se pueden encontrar muchas otras pruebas en otros artículos . Existen pruebas de que las estadísticas de prueba son apropiadas. [2]