


Una isocuanta (derivada de cantidad y la palabra griega isos , ίσος , que significa "igual"), en microeconomía , es una línea de contorno dibujada a través del conjunto de puntos en los que se produce la misma cantidad de producto mientras cambian las cantidades de dos o más insumos. [1] [2] Los ejes x e y en una isocuanta representan dos insumos relevantes, que suelen ser un factor de producción como el trabajo, el capital, la tierra o la organización. Una isocuanta también puede conocerse como una "curva de isoproducto" o una "curva de igual producto".
Mientras que una curva de indiferencia ayuda a resolver el problema de maximización de la utilidad de los consumidores, la curva isocuanta se ocupa del problema de minimización de costos y maximización de ganancias y producción de los productores. Las curvas de indiferencia difieren de las isocuantas en que no pueden ofrecer una medición precisa de la utilidad, solo su relevancia en relación con una línea base. Mientras que, a partir de una isocuanta, el producto se puede medir con precisión en unidades físicas y se sabe exactamente en qué medida la isocuanta 1 excede a la isocuanta 2.
En economía gerencial, las isocuantas se dibujan típicamente junto con las curvas de isocosto en los gráficos capital-trabajo , mostrando el equilibrio tecnológico entre capital y trabajo en la función de producción , y los retornos marginales decrecientes de ambos insumos. En economía gerencial, la unidad de isocuanta es comúnmente el neto del costo de capital. Como tal, las isocuantas por naturaleza son de pendiente negativa debido al funcionamiento de las tasas marginales decrecientes de sustitución técnica (TMTS). [3] [4] La pendiente de una isocuanta representa la tasa a la que el insumo x puede sustituirse por el insumo y. [5] Este concepto es la TMTS, por lo que TMTS = pendiente de la isocuanta. Por lo tanto, cuanto más empinada sea la isocuanta, mayor será la TMTS. Dado que la TMTS debe disminuir, las isocuantas deben ser convexas a su origen. Agregar un insumo mientras se mantiene constante el otro eventualmente conduce a una producción marginal decreciente.
La línea de contorno de una isocuanta representa cada combinación de dos factores que maximizan por completo el uso de los recursos de una empresa (como el presupuesto o el tiempo). La maximización total de los recursos suele considerarse "eficiente". La asignación eficiente de los factores de producción solo se produce cuando dos isocuantas son tangentes entre sí. Si una empresa produce a la izquierda de la línea de contorno, se considera que está operando de manera ineficiente, porque no está maximizando el uso de sus recursos disponibles. [6] Una empresa no puede producir a la derecha de la línea de contorno a menos que exceda sus restricciones.
Una familia de isocuantas puede representarse mediante un mapa de isocuantas , un gráfico que combina varias isocuantas, cada una de las cuales representa una cantidad diferente de producción. Un mapa de isocuantas puede indicar rendimientos decrecientes o crecientes a escala en función del aumento o la disminución de las distancias entre los pares de isocuantas de incremento de producción fijo, a medida que aumenta la producción. [7] Si la distancia entre esas isocuantas aumenta a medida que aumenta la producción, la función de producción de la empresa exhibe rendimientos decrecientes a escala; duplicar ambos insumos dará como resultado la ubicación en una isocuanta con menos del doble de la producción de la isocuanta anterior. Por el contrario, si la distancia disminuye a medida que aumenta la producción, la empresa está experimentando rendimientos crecientes a escala; duplicar ambos insumos da como resultado la ubicación en una isocuanta con más del doble de la producción de la isocuanta original. Una empresa puede optar por utilizar la información que proporciona una isocuanta sobre los rendimientos a escala , utilizándola como una idea de cómo asignar recursos. [8]

Saber cómo asignar recursos es un concepto pertinente para la economía gerencial. Las isocuantas pueden ser útiles para representar gráficamente esta cuestión de la escasez . Muestran hasta qué punto la empresa en cuestión tiene la capacidad de sustituir entre dos insumos diferentes (x e y en el gráfico) a voluntad para producir el mismo nivel de producción (véase: Gráfico C)). También representan diferentes combinaciones de cantidades de dos bienes que se adhieren a una restricción presupuestaria . Por lo tanto, pueden usarse como una herramienta para ayudar a la gerencia a tomar decisiones mejor informadas con respecto a dilemas de producción y ganancias, como la minimización de costos o desperdicios y la maximización de ingresos y producción.
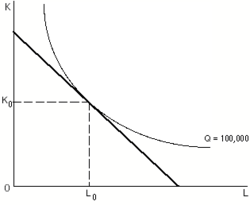
Una empresa puede determinar la combinación de insumos de menor costo para producir un producto dado, combinando curvas de isocosto e isocuantas, y adhiriéndose a las Condiciones de Primer Orden . [3] La combinación de menor costo es aquella en la que la relación de productos marginales es igual a la relación de precios de los factores. En este punto, la pendiente de la isocuanta y la pendiente del isocosto serán iguales (ver intersección del gráfico D). Una empresa tiene incentivos para producir en la combinación de menor costo porque es en este punto en el que los costos relacionados de la producción deseada se minimizan. [9]
Al igual que con las curvas de indiferencia, dos isocuantas nunca pueden cruzarse. Además, cada combinación posible de insumos se encuentra en una isocuanta. Por último, cualquier combinación de insumos por encima o a la derecha de una isocuanta representa un nivel más alto de producción, y viceversa. Aunque el producto marginal de un insumo disminuye a medida que se aumenta la cantidad del insumo mientras se mantienen constantes todos los demás insumos, el producto marginal nunca es negativo en el rango observado empíricamente, ya que una empresa racional nunca aumentaría un insumo para disminuir la producción.
Si los dos insumos son sustitutos perfectos, el mapa de isocuantas resultante se representa en la figura A; con un nivel dado de producción Q3, el insumo X puede ser reemplazado por el insumo Y a una tasa invariable. Los insumos sustitutos perfectos no experimentan tasas marginales de retorno decrecientes cuando se sustituyen entre sí en la función de producción.
Si los dos insumos son complementos perfectos, el mapa de isocuantas toma la forma de la figura B; con un nivel de producción Q3, el insumo X y el insumo Y solo pueden combinarse eficientemente en la proporción determinada que se da en el punto de inflexión de la isocuanta. La empresa combinará los dos insumos en la proporción requerida para maximizar las ganancias.
Las isocuantas se suelen combinar con líneas de isocosto para resolver un problema de minimización de costes para un nivel dado de producción. En el caso típico que se muestra en la figura superior, con isocuantas de curvas suaves, una empresa con costes unitarios fijos de los insumos tendrá curvas de isocosto lineales y con pendiente negativa; cualquier punto de tangencia entre una isocuanta y una curva de isocosto representa la combinación de insumos que minimiza los costes para producir el nivel de producción asociado con esa isocuanta. Una línea que une los puntos de tangencia de las isocuantas y los isocostos (con los precios de los insumos constantes) se denomina trayectoria de expansión . [10]
Suponiendo que la tasa marginal de sustitución técnica es decreciente y, por lo tanto, que la elasticidad de sustitución es positiva y finita, la isocuanta es convexa respecto del origen. Puede producirse una isocuanta localmente no convexa si en uno de los insumos hay rendimientos de escala suficientemente fuertes. En este caso, hay una elasticidad de sustitución negativa: a medida que aumenta la relación entre el insumo A y el insumo B, el producto marginal de A respecto de B aumenta en lugar de disminuir.
Una isocuanta no convexa tiende a producir cambios grandes y discontinuos en la combinación de insumos que minimizan el precio en respuesta a los cambios de precio. Consideremos, por ejemplo, el caso en el que la isocuanta es globalmente no convexa y la curva de isocosto es lineal. En este caso, la combinación de insumos con costo mínimo será una solución de esquina e incluirá solo un insumo (por ejemplo, el insumo A o el insumo B). La elección de qué insumo utilizar dependerá de los precios relativos. En alguna relación de precios crítica, la combinación óptima de insumos cambiará de todos los insumos A a todos los insumos B y viceversa en respuesta a un pequeño cambio en los precios relativos.
{{cite web}}: Falta o está vacío |title=( ayuda )