Ecualización de histograma

Método de procesamiento de imágenes para ajustar el contraste utilizando el histograma de la imagen

La ecualización de histograma es un método de procesamiento de imágenes para ajustar el contraste utilizando el histograma de la imagen .

Histogramas de una imagen antes y después de la ecualización.

Descripción general

Este método suele aumentar el contraste global de muchas imágenes, especialmente cuando la imagen está representada por un rango estrecho de valores de intensidad. Mediante este ajuste, las intensidades se pueden distribuir mejor en el histograma utilizando el rango completo de intensidades de manera uniforme. Esto permite que las áreas de menor contraste local obtengan un mayor contraste. La ecualización del histograma logra esto al distribuir de manera efectiva los valores de intensidad altamente poblados que se utilizan para degradar el contraste de la imagen.

El método es útil en imágenes con fondos y primeros planos que son a la vez brillantes o ambos oscuros. En particular, el método puede conducir a mejores vistas de la estructura ósea en imágenes de rayos X y a mejores detalles en fotografías que están sobre o subexpuestas. Una ventaja clave del método es que es una técnica bastante sencilla que se adapta a la imagen de entrada y un operador invertible . Por lo tanto, en teoría, si se conoce la función de ecualización del histograma , se puede recuperar el histograma original. El cálculo no es computacionalmente intensivo. Una desventaja del método es que es indiscriminado. Puede aumentar el contraste del ruido de fondo , mientras que disminuye la señal utilizable .

En las imágenes científicas donde la correlación espacial es más importante que la intensidad de la señal (como la separación de fragmentos de ADN de longitud cuantificada), la pequeña relación señal-ruido generalmente dificulta las detecciones visuales.

La ecualización de histograma a menudo produce efectos poco realistas en las fotografías; sin embargo, es muy útil para imágenes científicas como imágenes térmicas , satelitales o de rayos X , a menudo la misma clase de imágenes a las que se aplicaría un color falso . Además, la ecualización de histograma puede producir efectos no deseados (como gradiente de imagen visible ) cuando se aplica a imágenes con baja profundidad de color . Por ejemplo, si se aplica a una imagen de 8 bits mostrada con una paleta de escala de grises de 8 bits, reducirá aún más la profundidad de color (número de tonos de gris únicos) de la imagen. La ecualización de histograma funcionará mejor cuando se aplique a imágenes con una profundidad de color mucho mayor que el tamaño de la paleta , como datos continuos o imágenes en escala de grises de 16 bits.

Hay dos formas de pensar e implementar la ecualización del histograma: como cambio de imagen o como cambio de paleta . La operación se puede expresar como P(M(I)), donde I es la imagen original, M es la operación de mapeo de ecualización del histograma y P es una paleta. Si definimos una nueva paleta como P'=P(M) y dejamos la imagen I sin cambios, la ecualización del histograma se implementa como cambio de paleta o cambio de mapeo. Por otro lado, si la paleta P permanece sin cambios y la imagen se modifica a I'=M(I) , la implementación se logra mediante un cambio de imagen. En la mayoría de los casos, el cambio de paleta es mejor ya que conserva los datos originales.

Las modificaciones de este método utilizan múltiples histogramas, llamados subhistogramas, para enfatizar el contraste local, en lugar del contraste global general. Algunos ejemplos de estos métodos incluyen la ecualización de histograma adaptativa , la ecualización de histograma adaptativa con limitación de contraste o CLAHE , la ecualización de histograma multipico (MPHE) y la ecualización de bihistograma optimizada beta multipropósito (MBOBHE). El objetivo de estos métodos, especialmente MBOBHE, es mejorar el contraste sin producir artefactos de pérdida de detalle y desplazamiento de la media del brillo modificando el algoritmo HE. ^[1]

En las redes neuronales biológicas también parece ocurrir una transformación de señal equivalente a la ecualización del histograma, con el fin de maximizar la tasa de activación de salida de la neurona en función de las estadísticas de entrada. Esto se ha demostrado en particular en la retina de la mosca . ^[2]

La ecualización de histogramas es un caso específico de la clase más general de métodos de reasignación de histogramas. Estos métodos buscan ajustar la imagen para facilitar su análisis o mejorar la calidad visual (por ejemplo, retinex ).

Proyección posterior

La retroproyección (o "proyecto") de una imagen histogramada es la reaplicación del histograma modificado a la imagen original, funcionando como una tabla de consulta para los valores de brillo de los píxeles.

Para cada grupo de píxeles tomados de la misma posición de todas las imágenes monocanales de entrada, la función asigna el valor del bin del histograma a la imagen de destino, donde las coordenadas del bin están determinadas por los valores de los píxeles en este grupo de entrada. En términos estadísticos, el valor de cada píxel de la imagen de salida caracteriza la probabilidad de que el grupo de píxeles de entrada correspondiente pertenezca al objeto cuyo histograma se utiliza. ^[3]

Implementación

Considere una imagen en escala de grises discreta { x } y sea n _i el número de ocurrencias del nivel de gris i . La probabilidad de una ocurrencia de un píxel de nivel i en la imagen es

${\displaystyle \ p_{x}(i)=p(x=i)={\frac {n_{i}}{n}},\quad 0\leq i<L}$

${\displaystyle \ L}$siendo el número total de niveles de gris en la imagen (normalmente 256), n es el número total de píxeles en la imagen y, de hecho, el histograma de la imagen para el valor de píxel i, normalizado a [0,1]. ${\displaystyle p_{x}(i)}$

Definamos también la función de distribución acumulativa correspondiente a i como

${\displaystyle \operatorname {cdf} _{x}(i)=\sum _{j=0}^{i}p_{x}(x=j)}$,

que es también el histograma normalizado acumulado de la imagen.

Nos gustaría crear una transformación de la forma para producir una nueva imagen { y }, con un histograma plano. Dicha imagen tendría una función de distribución acumulativa linealizada (CDF) en todo el rango de valores, es decir ${\displaystyle \ y=T(x)}$

${\displaystyle \operatorname {cdf} _{y}(i)=(i+1)K}$para ${\displaystyle 0\leq i<L}$

para alguna constante . Las propiedades de la CDF nos permiten realizar dicha transformación (ver Función de distribución inversa ); se define como ${\displaystyle \ K}$

${\displaystyle \ y=T(k)=\operatorname {cdf} _{x}(k)}$

donde está en el rango . Observe que asigna los niveles al rango [0,1], ya que usamos un histograma normalizado de { x }. Para asignar los valores nuevamente a su rango original, se debe aplicar la siguiente transformación simple al resultado: ${\displaystyle \ k}$ ${\displaystyle [0,L-1])}$ ${\displaystyle \ T}$

${\displaystyle \ y^{\prime }=y\cdot (\max\{x\}-\min\{x\})+\min\{x\}=y\cdot (L-1)}$.

Se proporciona una derivación más detallada en Matemáticas 77C de la Universidad de California, Irvine: Ecualización de histograma.

${\displaystyle \ y}$es un valor real mientras que debe ser un entero. Un método intuitivo y popular ^[4] es aplicar la operación de redondeo: ${\displaystyle \ y^{\prime }}$

${\displaystyle \ y^{\prime }=\operatorname {round} (y\cdot (L-1))}$.

Sin embargo, el análisis detallado da como resultado una formulación ligeramente diferente. El valor asignado debe ser 0 para el rango de . Y para , para , ...., y finalmente para . Entonces la fórmula de cuantificación de a debe ser ${\displaystyle \ y^{\prime }}$ ${\displaystyle 0<y\leq 1/L}$ ${\displaystyle \ y^{\prime }=1}$ ${\displaystyle 1/L<y\leq 2/L}$ ${\displaystyle \ y^{\prime }=2}$ ${\displaystyle 2/L<y\leq 3/L}$ ${\displaystyle \ y^{\prime }=L-1}$ ${\displaystyle (L-1)/L<y\leq 1}$ ${\displaystyle \ y}$ ${\displaystyle \ y^{\prime }}$

${\displaystyle y^{\prime }=\operatorname {ceil} (L\cdot y)-1}$.

(Nota: cuando , sin embargo, no sucede simplemente porque significa que no hay ningún píxel correspondiente a ese valor). ${\displaystyle y^{\prime }=-1}$ ${\displaystyle \ y=0}$ ${\displaystyle \ y=0}$

De imágenes en color

Lo anterior describe la ecualización de histograma en una imagen en escala de grises. Sin embargo, también se puede utilizar en imágenes en color aplicando el mismo método por separado a los componentes rojo, verde y azul de los valores de color RGB de la imagen. Sin embargo, aplicar el mismo método en los componentes rojo, verde y azul de una imagen RGB puede producir cambios dramáticos en el balance de color de la imagen , ya que las distribuciones relativas de los canales de color cambian como resultado de la aplicación del algoritmo. Sin embargo, si la imagen se convierte primero a otro espacio de color, espacio de color Lab o espacio de color HSL/HSV en particular, entonces el algoritmo se puede aplicar al canal de luminancia o valor sin que se produzcan cambios en el tono y la saturación de la imagen. ^[5] Existen varios métodos de ecualización de histograma en el espacio 3D. Trahanias y Venetsanopoulos aplicaron la ecualización de histograma en el espacio de color 3D ^[6] Sin embargo, da como resultado un "blanqueamiento" donde la probabilidad de píxeles brillantes es mayor que la de los oscuros. ^[7] Han et al. Se propuso utilizar una nueva cdf definida por el plano de isoluminancia, que da como resultado una distribución de gris uniforme. ^[8]

Ejemplos

Para mantener la coherencia con el uso estadístico , "CDF" (es decir, función de distribución acumulativa) debería reemplazarse por "histograma acumulativo", especialmente porque el artículo hace referencia a la función de distribución acumulativa , que se obtiene dividiendo los valores del histograma acumulativo por la cantidad total de píxeles. La CDF ecualizada se define en términos de rango como . ${\displaystyle rank/pixelcount}$

Imagen pequeña

La subimagen 8×8 se muestra en escala de grises de 8 bits

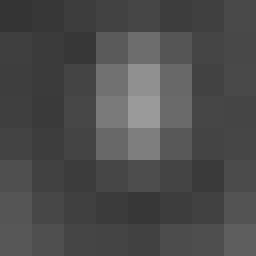
La imagen en escala de grises de 8 bits que se muestra tiene los siguientes valores:

El histograma de esta imagen se muestra en la siguiente tabla. Los valores de píxeles que tienen un recuento de cero se excluyen por razones de brevedad.

A continuación se muestra la función de distribución acumulativa (cdf). Nuevamente, los valores de píxeles que no contribuyen a un aumento de la cdf se excluyen para abreviar.

(Tenga en cuenta que la versión aún no está ilustrada). ${\displaystyle h(v)=\operatorname {ceil} (\operatorname {cdf} (v))-1}$

Esta función de distribución de datos muestra que el valor mínimo en la subimagen es 52 y el valor máximo es 154. La función de distribución de datos de 64 para el valor 154 coincide con el número de píxeles de la imagen. La función de distribución de datos debe normalizarse a . La fórmula general de ecualización del histograma es: ${\displaystyle [0,255]}$

${\displaystyle h(v)=\mathrm {round} \left({\frac {\operatorname {cdf} (v)-\operatorname {cdf} _{\min }}{(M\times N)-\operatorname {cdf} _{\min }}}\times (L-1)\right)}$

donde cdf _min es el valor mínimo distinto de cero de la función de distribución acumulativa (en este caso 1), M × N da el número de píxeles de la imagen (para el ejemplo anterior 64, donde M es el ancho y N la altura) y L es el número de niveles de gris utilizados (en la mayoría de los casos, como este, 256).

Tenga en cuenta que para escalar los valores de los datos originales que están por encima de 0 en el rango de 1 a L-1, inclusive, la ecuación anterior sería:

${\displaystyle h(v)=\mathrm {round} \left({\frac {\operatorname {cdf} (v)-\operatorname {cdf} _{\min }}{(M\times N)-\operatorname {cdf} _{\min }}}\times (L-2)\right)+1}$

donde cdf(v) > 0. La escala de 1 a 255 preserva la no nulidad del valor mínimo.

La fórmula de ecualización para el ejemplo de escalado de datos de 0 a 255, inclusive, es:

${\displaystyle h(v)=\mathrm {round} \left({\frac {\operatorname {cdf} (v)-1}{63}}\times 255\right)}$

Por ejemplo, la cdf de 78 es 46. (El valor de 78 se utiliza en la fila inferior de la séptima columna). El valor normalizado se convierte en

${\displaystyle h(78)=\mathrm {round} \left({\frac {46-1}{63}}\times 255\right)=\mathrm {round} \left(0.714286\times 255\right)=182}$

Una vez hecho esto, los valores de la imagen ecualizada se toman directamente de la CDF normalizada para obtener los valores ecualizados:

Tenga en cuenta que el valor mínimo (52) ahora es 0 y el valor máximo (154) ahora es 255.

Imagen de tamaño completo

Véase también

• Coincidencia de histogramas
• Ecualización de histograma adaptativo
• Normalización (procesamiento de imágenes)
• Procesamiento de imágenes digitales
• Segmentación de imágenes

Referencias

1. Hum, Yan Chai; Lai, Khin Wee; Mohamad Salim, Maheza Irna (11 de octubre de 2014). "Ecualización de bihistogramas multiobjetivos para la mejora del contraste de la imagen". Complejidad . 20 (2): 22–36. Código Bibliográfico :2014Cmplx..20b..22H. doi :10.1002/cplx.21499.
2. Laughlin, SB (1981). "Un procedimiento de codificación simple mejora la capacidad de información de una neurona". Z. Naturforsch . 9–10(36):910–2.
3. Intel Corporation (2001). «Open Source Computer Vision Library Reference Manual» (PDF) . Archivado desde el original (PDF) el 9 de abril de 2015. Consultado el 11 de enero de 2015 . {{cite journal}}: Requiere citar revista |journal=( ayuda )
4. González, Rafael C. (2018). Procesamiento de imágenes digitales. Richard E. Woods (4ª ed.). Nueva York, Nueva York: Pearson. págs. 138-140. ISBN 978-1-292-22304-9.OCLC 991765590  .
5. S. Naik y C. Murthy, "Mejora de la imagen en color con preservación del tono sin problemas de gama", IEEE Trans. Image Processing, vol. 12, n.º 12, págs. 1591-1598, diciembre de 2003
6. PE Trahanias y AN Venetsanopoulos, "Mejora de imágenes en color mediante ecualización de histogramas 3D", en Proc. 15th IAPR Int. Conf. Pattern Recognition, vol. 1, págs. 545–548, agosto-septiembre de 1992.
7. N. Bassiou y C. Kotropoulos, "Ecualización del histograma de imagen en color mediante reducción de descuento absoluto", Computer Vision and Image Understanding, vol. 107, núm. 1-2, págs. 108-122, julio-agosto de 2007
8. Han, Ji-Hee; Yang, Sejung; Lee, Byung-Uk (2011). "Un nuevo método de ecualización de histograma de color 3-D con histograma de escala de grises 1-D uniforme". IEEE Transactions on Image Processing . 20 (2): 506–512. Bibcode :2011ITIP...20..506H. doi :10.1109/TIP.2010.2068555. PMID  20801744. S2CID  17972519.

• Acharya y Ray, Procesamiento de imágenes: principios y aplicaciones , Wiley-Interscience 2005 ISBN 0-471-71998-6 
• Russ, Manual de procesamiento de imágenes: cuarta edición , CRC 2002 ISBN 0-8493-2532-3 
• "Ecualización de histograma" en Generation5 (archivo)