La ecualización de histograma adaptativa (AHE) es una técnica de procesamiento de imágenes por computadora que se utiliza para mejorar el contraste de las imágenes. Se diferencia de la ecualización de histograma ordinaria en que el método adaptativo calcula varios histogramas , cada uno de los cuales corresponde a una sección distinta de la imagen, y los utiliza para redistribuir los valores de luminosidad de la imagen. Por lo tanto, es adecuada para mejorar el contraste local y mejorar las definiciones de los bordes en cada región de una imagen.
Sin embargo, la AHE tiene una tendencia a sobreamplificar el ruido en regiones relativamente homogéneas de una imagen. Una variante de la ecualización de histograma adaptativa denominada ecualización de histograma adaptativa limitada por contraste (CLAHE) evita esto al limitar la amplificación.
La ecualización de histograma ordinaria utiliza la misma transformación derivada del histograma de la imagen para transformar todos los píxeles. Esto funciona bien cuando la distribución de los valores de los píxeles es similar en toda la imagen. Sin embargo, cuando la imagen contiene regiones que son significativamente más claras o más oscuras que la mayor parte de la imagen, el contraste en esas regiones no se mejorará lo suficiente.
La ecualización de histograma adaptativa (AHE) mejora esto al transformar cada píxel con una función de transformación derivada de una región vecina. Primero se desarrolló para su uso en pantallas de cabina de aviones. [1] citado en [2] En su forma más simple, cada píxel se transforma en función del histograma de un cuadrado que rodea el píxel, como en la figura siguiente. La derivación de las funciones de transformación a partir de los histogramas es exactamente la misma que para la ecualización de histograma ordinaria : la función de transformación es proporcional a la función de distribución acumulativa (CDF) de los valores de los píxeles en la vecindad.
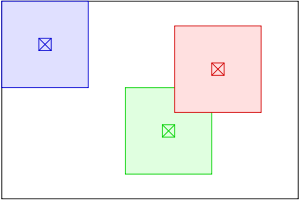
Los píxeles que se encuentran cerca del límite de la imagen deben tratarse de manera especial, ya que su vecindad no se encuentra completamente dentro de la imagen. Esto se aplica, por ejemplo, a los píxeles que se encuentran a la izquierda o por encima del píxel azul en la figura. Esto se puede solucionar ampliando la imagen reflejando las líneas y columnas de píxeles con respecto al límite de la imagen. Copiar simplemente las líneas de píxeles en el borde no es adecuado, ya que daría lugar a un histograma de vecindad con muchos picos.
La AHE ordinaria tiende a sobreamplificar el contraste en regiones casi constantes de la imagen, ya que el histograma en dichas regiones está altamente concentrado. Como resultado, la AHE puede causar que el ruido se amplifique en regiones casi constantes. La AHE limitada por contraste (CLAHE) es una variante de la ecualización de histograma adaptativa en la que se limita la amplificación del contraste, a fin de reducir este problema de amplificación del ruido. [3]
En AHE, la amplificación del contraste en la proximidad de un valor de píxel determinado se obtiene mediante la pendiente de la función de transformación. Esta es proporcional a la pendiente de la función de distribución acumulativa de proximidad (CDF) y, por lo tanto, al valor del histograma en ese valor de píxel. CLAHE limita la amplificación recortando el histograma en un valor predefinido antes de calcular la CDF. Esto limita la pendiente de la CDF y, por lo tanto, de la función de transformación. El valor en el que se recorta el histograma, el llamado límite de recorte, depende de la normalización del histograma y, por lo tanto, del tamaño de la región de proximidad. Los valores comunes limitan la amplificación resultante a entre 3 y 4.
Es ventajoso no descartar la parte del histograma que excede el límite de recorte, sino redistribuirla equitativamente entre todos los compartimentos del histograma. [3]
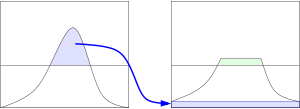
La redistribución hará que algunos contenedores superen nuevamente el límite de recorte (región sombreada en verde en la figura), lo que dará como resultado un límite de recorte efectivo que es mayor que el límite prescrito y cuyo valor exacto depende de la imagen. Si esto no es deseable, el procedimiento de redistribución se puede repetir de forma recursiva hasta que el exceso sea insignificante.
La ecualización de histograma adaptativo en su forma sencilla presentada anteriormente, tanto con limitación de contraste como sin ella, requiere el cálculo de un histograma de vecindad y una función de transformación diferentes para cada píxel de la imagen, lo que hace que el método sea muy costoso desde el punto de vista computacional.
La interpolación permite una mejora significativa en la eficiencia sin comprometer la calidad del resultado. [3] La imagen se divide en mosaicos rectangulares de igual tamaño como se muestra en la parte derecha de la figura a continuación. (64 mosaicos en 8 columnas y 8 filas es una opción común. [4] ). Luego se calcula un histograma, CDF y función de transformación para cada uno de los mosaicos. Las funciones de transformación son apropiadas para los píxeles del centro del mosaico (cuadrados negros en la parte izquierda de la figura). Todos los demás píxeles se transforman con hasta cuatro funciones de transformación de los mosaicos con píxeles centrales más cercanos a ellos, y se les asignan valores interpolados. Los píxeles en la mayor parte de la imagen (sombreados en azul) se interpolan bilinealmente , los píxeles cercanos al límite (sombreados en verde) se interpolan linealmente y los píxeles cerca de las esquinas (sombreados en rojo) se transforman con la función de transformación del mosaico de la esquina. Los coeficientes de interpolación reflejan la ubicación de los píxeles entre los píxeles del centro del mosaico más cercano, de modo que el resultado es continuo a medida que el píxel se acerca al centro del mosaico.
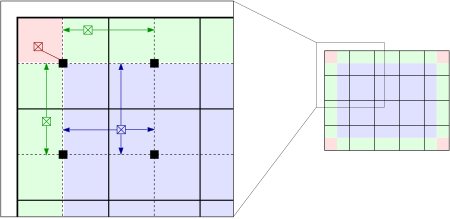
Este procedimiento reduce drásticamente el número de funciones de transformación a calcular y solo impone el pequeño costo adicional de la interpolación lineal.
Una alternativa al mosaico de la imagen es "deslizar" el rectángulo un píxel a la vez, y solo actualizar incrementalmente el histograma para cada píxel, [5] agregando la nueva fila de píxeles y restando la fila que queda atrás. El algoritmo se denomina SWAHE (Ecualización de histograma adaptativo de ventana deslizante) por los autores originales. La complejidad computacional del cálculo del histograma se reduce entonces de O ( N² ) a O ( N ) (siendo N = ancho de píxel del rectángulo circundante); y dado que no hay mosaico, no se requiere un paso de interpolación final.
6. GR Vidhya y H. Ramesh, "Efectividad de la técnica de ecualización de histograma adaptativo con contraste limitado en imágenes satelitales multiespectrales", Proc. Int. Conf. Video Image Process., págs. 234-239, diciembre de 2017.