- Gráficos circulares del "Breviario estadístico" de William Playfair, 1801
- Uno de los primeros gráficos circulares, 1801
- Mapa de Minard, 1858
- Carta polar de Florence Nightingale , 1858
Un gráfico circular (o gráfico circular ) es un gráfico estadístico circular que se divide en porciones para ilustrar la proporción numérica. En un gráfico circular, la longitud del arco de cada porción (y, en consecuencia, su ángulo central y área ) es proporcional a la cantidad que representa. Si bien se lo llama así por su parecido con una tarta que ha sido cortada en porciones, existen variaciones en la forma en que se puede presentar. El gráfico circular más antiguo conocido generalmente se atribuye al Breviario estadístico de William Playfair de 1801. [1] [2]
Los gráficos circulares son muy utilizados en el mundo empresarial y en los medios de comunicación. [3] Sin embargo, han sido criticados, [4] y muchos expertos recomiendan evitarlos, [5] [6] [7] [8] ya que la investigación ha demostrado que es difícil comparar diferentes secciones de un gráfico circular determinado, o comparar datos entre diferentes gráficos circulares. Los gráficos circulares se pueden reemplazar en la mayoría de los casos por otros gráficos como el gráfico de barras , el gráfico de cajas , el gráfico de puntos , etc.
El gráfico circular más antiguo conocido se atribuye generalmente al Breviario estadístico de William Playfair de 1801, en el que se utilizan dos gráficos de este tipo. [1] [2] [9] Playfair presentó una ilustración que contenía una serie de gráficos circulares. Uno de esos gráficos representaba las proporciones del Imperio turco ubicado en Asia , Europa y África antes de 1789. Esta invención no se utilizó ampliamente al principio. [1]
Playfair pensó que los gráficos circulares necesitaban una tercera dimensión para agregar información adicional. [10]
Florence Nightingale no inventó el gráfico circular, pero lo adaptó para hacerlo más legible, lo que fomentó su uso generalizado, todavía hoy. Nightingale reconfiguró el gráfico circular haciendo que la longitud de las cuñas fuera variable en lugar de su ancho. El gráfico, entonces, se parecía a una cresta de gallo . [11] Más tarde se asumió que lo había creado debido a la oscuridad y la falta de practicidad de la creación de Playfair. [12] El diagrama de área polar de Nightingale , [13] : 107 u ocasionalmente el diagrama de rosa de Nightingale , equivalente a un histograma circular moderno , para ilustrar las fuentes estacionales de mortalidad de pacientes en el hospital de campaña militar que ella dirigía, se publicó en Notes on Matters Affecting the Health, Efficiency, and Hospital Administration of the British Army y se envió a la reina Victoria en 1858. Según el historiador Hugh Small, "ella puede haber sido la primera en usar [gráficos circulares] para persuadir a la gente de la necesidad de un cambio". [11]
El ingeniero francés Charles Joseph Minard también utilizó gráficos circulares, en 1858. Un mapa suyo de 1858 utilizó gráficos circulares para representar el ganado enviado desde toda Francia para su consumo en París .
Un gráfico circular en 3D, o gráfico circular en perspectiva, se utiliza para dar al gráfico un aspecto tridimensional . A menudo se utiliza por razones estéticas, pero la tercera dimensión no mejora la lectura de los datos; por el contrario, estos gráficos son difíciles de interpretar debido al efecto distorsionador de la perspectiva asociado con la tercera dimensión. El uso de dimensiones superfluas que no se utilizan para mostrar los datos de interés se desaconseja para los gráficos en general, no solo para los gráficos circulares. [7] [14]
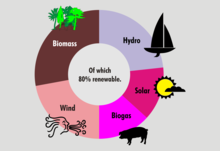
Un gráfico de anillos (también escrito donut) es una variante del gráfico circular, con un centro en blanco que permite incluir información adicional sobre los datos en su conjunto. [15] [16] Los gráficos de anillos son similares a los gráficos circulares en que su objetivo es ilustrar proporciones. [ cita requerida ] Este tipo de gráfico circular puede admitir múltiples estadísticas a la vez y proporciona una mejor relación de intensidad de datos que los gráficos circulares estándar. [16] No tiene que contener información en el centro.
Un gráfico con uno o más sectores separados del resto del disco se conoce como gráfico circular despiezado . Este efecto se utiliza para resaltar un sector o para resaltar segmentos más pequeños del gráfico con proporciones pequeñas.

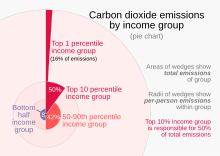
El diagrama de área polar es similar a un gráfico circular habitual, excepto que los sectores tienen ángulos iguales y difieren más bien en la distancia que cada sector se extiende desde el centro del círculo. El diagrama de área polar se utiliza para representar gráficamente fenómenos cíclicos (por ejemplo, recuentos de muertes por mes). Por ejemplo, si se van a representar gráficamente los recuentos de muertes en cada mes durante un año, habrá 12 sectores (uno por mes), todos con el mismo ángulo de 30 grados cada uno. El radio de cada sector sería proporcional a la raíz cuadrada de la tasa de mortalidad del mes, por lo que el área de un sector representa la tasa de muertes en un mes. Si la tasa de mortalidad en cada mes se subdivide por causa de muerte, es posible hacer múltiples comparaciones en un diagrama, como se ve en el diagrama de área polar desarrollado famosamente por Florence Nightingale .
El primer uso conocido de diagramas de área polar fue realizado por André-Michel Guerry , a los que llamó courbes circulaires (curvas circulares), en un artículo de 1829 que mostraba la variación estacional y diaria en la dirección del viento a lo largo del año y los nacimientos y muertes por hora del día. [17] Léon Lalanne utilizó más tarde un diagrama polar para mostrar la frecuencia de las direcciones del viento alrededor de los puntos cardinales en 1843. Los meteorólogos todavía utilizan la rosa de los vientos . Nightingale publicó su diagrama de rosa en 1858. Aunque el nombre "coxcomb" se ha asociado con este tipo de diagrama, Nightingale originalmente usó el término para referirse a la publicación en la que apareció por primera vez este diagrama (un libro de gráficos y tablas que llamaba la atención) en lugar de a este tipo específico de diagrama. [18]
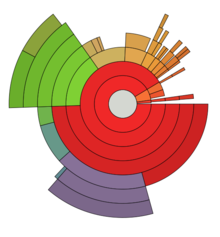
Un gráfico de anillos, también conocido como gráfico de rayos de sol o gráfico circular de varios niveles, se utiliza para visualizar datos jerárquicos, representados por círculos concéntricos. [19] El círculo en el centro representa el nodo raíz, con la jerarquía moviéndose hacia afuera desde el centro. Un segmento del círculo interior tiene una relación jerárquica con aquellos segmentos del círculo exterior que se encuentran dentro del barrido angular del segmento principal. [20]
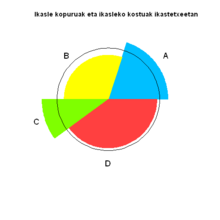
Una variante del gráfico de área polar es el gráfico de spie, diseñado por Dror Feitelson. [21] El diseño superpone un gráfico circular normal con un gráfico de área polar modificado para permitir la comparación de dos conjuntos de datos relacionados. El gráfico circular base representa el primer conjunto de datos de la forma habitual, con diferentes tamaños de porción. El segundo conjunto está representado por el gráfico de área polar superpuesto, utilizando los mismos ángulos que la base y ajustando los radios para que se ajusten a los datos. Por ejemplo, el gráfico circular base podría mostrar la distribución de grupos de edad y género en una población, y superponer su representación entre las víctimas de accidentes de tráfico. Los grupos de edad y género que son especialmente susceptibles a verse involucrados en accidentes se destacan como porciones que se extienden más allá del gráfico circular original.

Los gráficos cuadrados, también llamados gráficos de gofre, son una forma de gráficos circulares que utilizan cuadrados en lugar de círculos para representar porcentajes. Similares a los gráficos circulares básicos, los gráficos circulares cuadrados toman cada porcentaje de un total de 100%. Suelen ser cuadrículas de 10 por 10, donde cada celda representa el 1%. A pesar del nombre, se pueden utilizar círculos, pictogramas (como de personas) y otras formas en lugar de cuadrados. Una de las principales ventajas de los gráficos cuadrados es que se pueden representar fácilmente porcentajes más pequeños, difíciles de ver en los gráficos circulares tradicionales. [22]
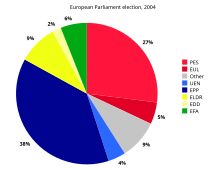
El siguiente gráfico de ejemplo se basa en los resultados preliminares de las elecciones al Parlamento Europeo de 2004. La tabla enumera el número de escaños asignados a cada grupo de partidos, junto con el porcentaje derivado del total que cada uno representa. Los valores de la última columna, el ángulo central derivado de cada sector, se obtienen tomando ese porcentaje de 360.
*Debido al redondeo , estos totales no suman 100 y 360.
El tamaño de cada ángulo central es proporcional al tamaño de la cantidad correspondiente, en este caso el número de escaños. Como la suma de los ángulos centrales tiene que ser 360°, el ángulo central para una cantidad que es una fracción Q del total es 360 Q grados. En el ejemplo, el ángulo central para el grupo más grande (Partido Popular Europeo (PPE)) es 135,7° porque 0,377 por 360, redondeado a un decimal, es igual a 135,7.

Un defecto que presentan los gráficos circulares es que no pueden mostrar más que unos pocos valores sin separar la codificación visual (las “porciones”) de los datos que representan (normalmente porcentajes). Cuando las porciones son demasiado pequeñas, los gráficos circulares tienen que depender de colores, texturas o flechas para que el lector pueda entenderlas. Esto los hace inadecuados para su uso con grandes cantidades de datos. Los gráficos circulares también ocupan una mayor cantidad de espacio en la página en comparación con los gráficos de barras más flexibles, que no necesitan tener leyendas separadas y pueden mostrar otros valores, como promedios u objetivos, al mismo tiempo. [7]
Los estadísticos generalmente consideran que los gráficos circulares son un método deficiente para mostrar información y no son comunes en la literatura científica. Una razón es que es más difícil hacer comparaciones entre el tamaño de los elementos de un gráfico cuando se utiliza el área en lugar de la longitud y cuando los diferentes elementos se muestran con formas diferentes. [23]
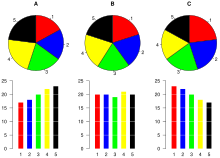
Además, en una investigación realizada en AT&T Bell Laboratories , se demostró que la comparación por ángulo era menos precisa que la comparación por longitud. La mayoría de los sujetos tienen dificultades para ordenar las porciones en el gráfico circular por tamaño; cuando se utiliza un gráfico de barras equivalente, la comparación es mucho más fácil. [24] De manera similar, las comparaciones entre conjuntos de datos son más fáciles utilizando el gráfico de barras. Sin embargo, si el objetivo es comparar una categoría dada (una porción del gráfico circular) con el total (el gráfico circular completo) en un solo gráfico y el múltiplo está cerca del 25 o 50 por ciento, entonces un gráfico circular a menudo puede ser más efectivo que un gráfico de barras. [25] [26]
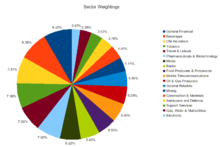
En un gráfico circular con muchas secciones, varios valores pueden representarse con colores iguales o similares, lo que dificulta la interpretación.

Varios estudios presentados en la Conferencia Europea de Visualización analizaron la precisión relativa de varios formatos de gráficos circulares, [27] [28] [22] llegando a la conclusión de que los gráficos circulares y los gráficos de anillos producen niveles de error similares al leerlos, y los gráficos circulares cuadrados proporcionan la lectura más precisa. [29]
{{cite book}}: |website=ignorado ( ayuda )