Gráfico de ciclo (álgebra)

Estructura gráfica estudiada en teoría de grupos.

En teoría de grupos , un subcampo del álgebra abstracta , un gráfico de ciclo de un grupo es un gráfico no dirigido que ilustra los diversos ciclos de ese grupo, dado un conjunto de generadores para el grupo. Los gráficos de ciclos son particularmente útiles para visualizar la estructura de pequeños grupos finitos .

Un ciclo es el conjunto de potencias de un elemento de grupo dado a , donde an , la ⁿ - ésima potencia de un elemento a , se define como el producto de a multiplicado por sí mismo n veces. Se dice que el elemento a genera el ciclo. En un grupo finito, alguna potencia distinta de cero de a debe ser la identidad del grupo , que denotamos como e o 1; el poder más bajo es el orden del elemento a , el número de elementos distintos en el ciclo que genera. En un gráfico de ciclo, el ciclo se representa como un polígono, cuyos vértices representan los elementos del grupo y sus aristas indican cómo están vinculados entre sí para formar el ciclo.

Definición

Cada elemento del grupo está representado por un nodo en el gráfico de ciclos, y se representan suficientes ciclos como polígonos en el gráfico para que cada nodo se encuentre en al menos un ciclo. Todos esos polígonos pasan por el nodo que representa la identidad, y algunos otros nodos también pueden encontrarse en más de un ciclo.

Supongamos que un elemento del grupo a genera un ciclo de orden 6 (tiene orden 6), de modo que los nodos a , a ² , a ³ , a ⁴ , a ⁵ y a ⁶ = e son los vértices de un hexágono en el ciclo. grafico. El elemento a ² tiene entonces orden 3; pero hacer que los nodos a ² , a ⁴ y e sean los vértices de un triángulo en el gráfico no agregaría información nueva. Así, sólo es necesario considerar los ciclos primitivos , aquellos que no son subconjuntos de otro ciclo. Además, el nodo a ⁵ , que también tiene orden 6, genera el mismo ciclo que a sí mismo; por lo que tenemos al menos dos opciones sobre qué elemento usar para generar un ciclo, a menudo más.

Para construir un gráfico de ciclo para un grupo, comenzamos con un nodo para cada elemento del grupo. Para cada ciclo primitivo, luego elegimos algún elemento a que genere ese ciclo, y conectamos el nodo de e con el de a , a con a ² , ..., a ^{k −1} con a ^k , etc., hasta que volviendo a e . El resultado es un gráfico de ciclo para el grupo.

Cuando un elemento del grupo a tiene orden 2 (de modo que la multiplicación por a es una involución ), la regla anterior conectaría e a a por dos aristas, una saliendo y la otra regresando. Excepto cuando la intención es enfatizar los dos bordes de dicho ciclo, normalmente se dibuja ^[1] como una sola línea entre los dos elementos.

Tenga en cuenta que esta correspondencia entre grupos y gráficos no es uno a uno en ninguna dirección: dos grupos diferentes pueden tener el mismo gráfico de ciclo y dos gráficos diferentes pueden ser gráficos de ciclo para un solo grupo. Damos ejemplos de cada uno en la sección de no unicidad.

Ejemplo y propiedades

Como ejemplo de un gráfico de ciclo de grupo, considere el grupo diédrico Dih ₄ . La tabla de multiplicar para este grupo se muestra a la izquierda y el gráfico del ciclo se muestra a la derecha, donde e especifica el elemento de identidad.

Observe el ciclo { e , a , a ² , a ³ } en la tabla de multiplicar, con a ⁴ = e . El inverso a ⁻¹ = a ³ también es un generador de este ciclo: ( a ³ ) ² = a ² , ( a ³ ) ³ = a y ( a ³ ) ⁴ = e . De manera similar, cualquier ciclo de cualquier grupo tiene al menos dos generadores y puede recorrerse en cualquier dirección. De manera más general, el número de generadores de un ciclo con n elementos viene dado por la función φ de Euler de n , y cualquiera de estos generadores puede escribirse como el primer nodo del ciclo (junto a la identidad e ); o más comúnmente los nodos se dejan sin marcar. Dos ciclos distintos no pueden cruzarse en un generador.

Gráfico de ciclo del grupo de cuaterniones Q ₈ .

Los ciclos que contienen un número no primo de elementos tienen subgrupos cíclicos que no se muestran en el gráfico. Para el grupo Dih ₄ anterior, podríamos trazar una línea entre a ² y e ya que ( a ² ) ² = e , pero como a ² es parte de un ciclo más grande, este no es un borde del gráfico del ciclo.

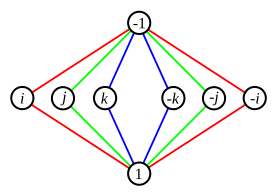
Puede haber ambigüedad cuando dos ciclos comparten un elemento no identitario. Por ejemplo, el grupo de cuaterniones de 8 elementos tiene el gráfico de ciclo que se muestra a la derecha. Cada uno de los elementos de la fila del medio, cuando se multiplica por sí mismo, da −1 (donde 1 es el elemento identidad). En este caso podemos usar diferentes colores para realizar un seguimiento de los ciclos, aunque las consideraciones de simetría también funcionarán.

Como se señaló anteriormente, los dos bordes de un ciclo de 2 elementos generalmente se representan como una sola línea.

El inverso de un elemento es el nodo simétrico a él en su ciclo, respecto de la reflexión que fija la identidad.

No unicidad

El gráfico de ciclo de un grupo no se determina de forma única hasta el isomorfismo del gráfico ; ni determina de forma única el grupo hasta el isomorfismo del grupo . Es decir, el gráfico obtenido depende del conjunto de generadores elegido, y dos grupos diferentes (con conjuntos de generadores elegidos) pueden generar el mismo gráfico de ciclo. ^[2]

Un mismo grupo puede tener diferentes gráficos de ciclo

Para algunos grupos, elegir diferentes elementos para generar los distintos ciclos primitivos de ese grupo puede conducir a diferentes gráficos de ciclos. Hay un ejemplo de esto para el grupo abeliano , que tiene orden 20. ^[2] Denotamos un elemento de ese grupo como un triple de números , donde y cada uno de y es 0 o 1. El triple es el elemento identidad. En los dibujos siguientes, se muestra arriba y . ${\displaystyle C_{5}\times C_{2}\times C_{2}}$ ${\displaystyle (i;j,k)}$ ${\displaystyle 0\leq i<5}$ ${\displaystyle j}$ ${\displaystyle k}$ ${\displaystyle (0;0,0)}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle k}$

Este grupo tiene tres ciclos primitivos, cada uno de orden 10. En el gráfico del primer ciclo, elegimos, como generadores de esos tres ciclos, los nodos , y . En el segundo, generamos el tercero de esos ciclos, el azul, comenzando con . ${\displaystyle (1;1,0)}$ ${\displaystyle (1;0,1)}$ ${\displaystyle (1;1,1)}$ ${\displaystyle (2;1,1)}$

Las dos gráficas resultantes no son isomorfas porque tienen diámetros 5 y 4 respectivamente.

Diferentes grupos pueden tener el mismo gráfico de ciclo.

Dos grupos diferentes (no isomorfos) pueden tener gráficos de ciclos que son isomorfos , donde el último isomorfismo ignora las etiquetas en los nodos de los gráficos. De ello se deduce que la estructura de un grupo no está determinada únicamente por su gráfico de ciclo.

Ya existe un ejemplo de esto para grupos de orden 16, siendo los dos grupos y . El grupo abeliano es el producto directo de los grupos cíclicos de órdenes 8 y 2. El grupo no abeliano es el producto semidirecto de y en el que el elemento de no identidad de se asigna al automorfismo multiplicado por 5 de . ${\displaystyle C_{8}\times C_{2}}$ ${\displaystyle C_{8}\rtimes _{5}C_{2}}$ ${\displaystyle C_{8}\times C_{2}}$ ${\displaystyle C_{8}\rtimes _{5}C_{2}}$ ${\displaystyle C_{8}}$ ${\displaystyle C_{2}}$ ${\displaystyle C_{2}}$ ${\displaystyle C_{8}}$

Al dibujar las gráficas de ciclo de esos dos grupos, consideramos que están generados por los elementos s y t con ${\displaystyle C_{8}\times C_{2}}$

${\displaystyle s^{8}=t^{2}=1\quad {\text{and}}\quad ts=st,}$

donde esa última relación se vuelve abeliana. Y suponemos que es generado por los elementos 𝜎 y 𝜏 con ${\displaystyle C_{8}\times C_{2}}$ ${\displaystyle C_{8}\rtimes _{5}C_{2}}$

${\displaystyle \sigma ^{8}=\tau ^{2}=1\quad {\text{and}}\quad \tau \sigma =\sigma ^{5}\tau .}$

Aquí hay gráficos de ciclos para esos dos grupos, donde elegimos generar el ciclo verde a la izquierda y generar ese ciclo a la derecha: ${\displaystyle st}$ ${\displaystyle \sigma \tau }$

En el gráfico de la derecha, el ciclo verde, después de pasar de 1 a , se mueve al lado de porque ${\displaystyle \sigma \tau }$ ${\displaystyle \sigma ^{6},}$

${\displaystyle (\sigma \tau )(\sigma \tau )=\sigma (\tau \sigma )\tau =\sigma (\sigma ^{5}\tau )\tau =\sigma ^{6}.}$

Historia

Los gráficos de ciclos fueron investigados por el teórico de números Daniel Shanks a principios de la década de 1950 como una herramienta para estudiar grupos multiplicativos de clases de residuos . ^[3] Shanks publicó por primera vez la idea en la primera edición de 1962 de su libro Problemas resueltos y no resueltos en teoría de números . ^[4] En el libro, Shanks investiga qué grupos tienen gráficos de ciclo isomórficos y cuándo un gráfico de ciclo es plano . ^[5] En la segunda edición de 1978, Shanks reflexiona sobre su investigación sobre los grupos de clases y el desarrollo del método del paso gigante del bebé : ^[6]

Los gráficos de ciclos han demostrado ser útiles cuando se trabaja con grupos abelianos finitos; y los he utilizado con frecuencia para orientarme en una estructura intrincada [77, p. 852], en la obtención de una relación multiplicativa deseada [78, p. 426], o en aislar algún subgrupo deseado [79].

Los gráficos de ciclos se utilizan como herramienta pedagógica en el libro de texto introductorio de Nathan Carter de 2009, Visual Group Theory . ^[7]

Características gráficas de familias de grupos particulares.

Ciertos tipos de grupos dan gráficos típicos:

Los grupos cíclicos Z _n , orden n , son un ciclo único graficado simplemente como un polígono de n lados con los elementos en los vértices:

When n is a prime number, groups of the form (Z_n)^m will have (n^m − 1)/(n − 1) n-element cycles sharing the identity element:

Dihedral groups Dih_n, order 2n consists of an n-element cycle and n 2-element cycles:

Dicyclic groups, Dic_n = Q_4n, order 4n:

Other direct products:

Symmetric groups – The symmetric group S_n contains, for any group of order n, a subgroup isomorphic to that group. Thus the cycle graph of every group of order n will be found in the cycle graph of S_n.
See example: Subgroups of S4

Extended example: Subgroups of the full octahedral group

The full octahedral group is the direct product ${\displaystyle S_{4}\times Z_{2}}$ of the symmetric group S₄ and the cyclic group Z₂.
Its order is 48, and it has subgroups of every order that divides 48.

In the examples below nodes that are related to each other are placed next to each other,
so these are not the simplest possible cycle graphs for these groups (like those on the right).

Como todos los gráficos, un gráfico de ciclo se puede representar de diferentes maneras para enfatizar diferentes propiedades. Las dos representaciones del gráfico del ciclo de S ₄ son un ejemplo de ello.

Ver también

• Lista de grupos pequeños
• gráfico de cayley

Referencias

1. Sarah Perkins (2000). "Gráficos de involución conmutante para A˜n, sección 2.2, p.3, primera figura" (PDF) . Birkbeck College, Malet Street, Londres, WC1E 7HX: Facultad de Economía, Matemáticas y Estadística . Consultado el 31 de enero de 2016 .{{cite web}}: Mantenimiento CS1: ubicación ( enlace )
2. Stanford, Caleb; Verret, Gabriel. "¿Es único el gráfico del ciclo de un grupo?". Intercambio de pilas de matemáticas .
3. Mangos 1978, pag. 246.
4. Mangos 1978, pag. xii.
5. Shanks 1978, págs. 83–98, 206–208.
6. Mangos 1978, pag. 225.
7. Carter, Nathan (2009), Teoría de grupos visuales , materiales de recursos para el aula, Asociación Matemática de América, ISBN 978-0-88385-757-1

• Skiena, S. (1990). Ciclos, estrellas y ruedas. Implementación de matemáticas discretas: combinatoria y teoría de grafos con Mathematica (págs. 144-147).
• Shanks, Daniel (1978) [1962], Problemas resueltos y no resueltos en teoría de números (2ª ed.), Nueva York: Chelsea Publishing Company, ISBN 0-8284-0297-3
• Pemmaraju, S. y Skiena, S. (2003). Ciclos, estrellas y ruedas. Matemática discreta computacional: combinatoria y teoría de grafos con Mathematica (págs. 248-249). Prensa de la Universidad de Cambridge.

enlaces externos

• Weisstein, Eric W. "Gráfico de ciclo". MundoMatemático .