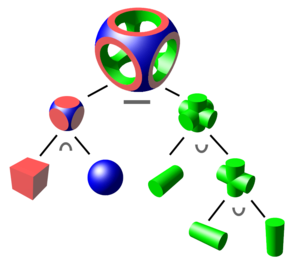
La geometría sólida constructiva ( CSG ; anteriormente llamada geometría sólida binaria computacional ) es una técnica utilizada en el modelado de sólidos . La geometría sólida constructiva permite a un modelador crear una superficie o un objeto complejo mediante el uso de operadores booleanos para combinar objetos más simples, [1] generando potencialmente objetos visualmente complejos mediante la combinación de algunos primitivos. [2] [3]
En los gráficos por computadora en 3D y en CAD , el CSG se utiliza a menudo en el modelado procedimental . El CSG también se puede realizar en mallas poligonales y puede ser procedimental y/o paramétrico o no.
Compare CSG con el modelado de malla poligonal y el modelado de cajas .
Los objetos sólidos más simples que se utilizan para la representación se denominan primitivos geométricos . Por lo general, son objetos de forma simple: cuboides , cilindros , prismas , pirámides , esferas , conos . [1] El conjunto de primitivos permitidos está limitado por cada paquete de software. Algunos paquetes de software permiten CSG en objetos curvos, mientras que otros no.
Un objeto se construye a partir de primitivos mediante operaciones permitidas , que son típicamente operaciones booleanas sobre conjuntos : unión , intersección y diferencia , así como transformaciones geométricas de esos conjuntos. [1]
Una primitiva puede describirse normalmente mediante un procedimiento que acepta una cierta cantidad de parámetros ; por ejemplo, una esfera puede describirse mediante las coordenadas de su punto central, junto con un valor de radio. Estas primitivas pueden combinarse en objetos compuestos mediante operaciones como las siguientes:
Combinando estas operaciones elementales es posible construir objetos de alta complejidad a partir de otros simples.
La representación de geometría sólida constructiva es particularmente sencilla cuando se utiliza el trazado de rayos . Los trazadores de rayos intersecan un rayo con ambos primitivos sobre los que se está operando, aplican el operador a los intervalos de intersección a lo largo del rayo 1D y luego toman el punto más cercano a la cámara a lo largo del rayo como resultado.

La geometría sólida constructiva tiene varios usos prácticos. Se utiliza en casos en los que se desean objetos geométricos simples, [ cita requerida ] o donde la precisión matemática es importante. [4] Casi todos los paquetes de CAD de ingeniería utilizan CSG (donde puede ser útil para representar cortes de herramientas y características donde las piezas deben encajar entre sí).
Tanto el motor Quake como el Unreal Engine utilizan este sistema, al igual que Hammer (el editor de niveles nativo del motor Source ) y Torque Game Engine / Torque Game Engine Advanced . CSG es popular porque un modelador puede usar un conjunto de objetos relativamente simples para crear una geometría muy complicada. [3] Cuando CSG es procedimental o paramétrico, el usuario puede revisar su geometría compleja cambiando la posición de los objetos o cambiando la operación booleana utilizada para combinar esos objetos.
Una de las ventajas de CSG es que puede asegurar fácilmente que los objetos son "sólidos" o herméticos si todas las formas primitivas son herméticas. [5] Esto puede ser importante para algunas aplicaciones de cálculo de ingeniería o fabricación. En comparación, al crear geometría basada en representaciones de límites , se requieren datos topológicos adicionales o se deben realizar comprobaciones de consistencia para asegurar que la descripción de límite dada especifique un objeto sólido válido. [1]
Una propiedad conveniente de las formas CSG es que es fácil clasificar puntos arbitrarios como si estuvieran dentro o fuera de la forma creada por CSG. El punto simplemente se clasifica en relación con todos los primitivos subyacentes y se evalúa la expresión booleana resultante. [6] Esta es una cualidad deseable para algunas aplicaciones como el trazado de rayos . [6]
Los modelos CSG, que se parametrizan por construcción, suelen ser más ventajosos que las mallas habituales en aplicaciones en las que el objetivo es fabricar modelos personalizados. Para este tipo de aplicaciones, puede resultar interesante convertir mallas ya existentes en árboles CSG. Este problema de conversión automática de mallas en árboles CSG se denomina CSG inverso .
Se requiere que el árbol CSG resultante ocupe el mismo volumen en el espacio 3D que la malla de entrada y que tenga una cantidad mínima de nodos. Se prefieren soluciones simples para garantizar que el modelo resultante sea fácil de editar. Resolver este problema es un desafío debido al gran espacio de búsqueda que se debe explorar. Combina parámetros continuos, como la dimensión y el tamaño de las formas primitivas, y parámetros discretos, como los operadores booleanos utilizados para construir el árbol CSG final.
Los métodos deductivos resuelven este problema construyendo un conjunto de semiespacios que describen el interior de la geometría. Estos semiespacios se utilizan para describir primitivas que pueden combinarse para obtener el modelo final. [7]
Otro enfoque desacopla la detección de formas primitivas y el cálculo del árbol CSG que define el modelo final. Este enfoque aprovecha la capacidad de las herramientas de síntesis de programas modernas para encontrar un árbol CSG con una complejidad mínima. [8]
También existen enfoques que utilizan algoritmos genéticos para optimizar iterativamente una forma inicial hacia la forma de la malla deseada. [9]