B-spline

Función spline

Curva spline dibujada como una suma ponderada de B-splines con puntos de control/polígono de control y curvas de componentes marcadas

En el subcampo matemático del análisis numérico , una B-spline o spline base es una función spline que tiene un soporte mínimo con respecto a un grado , suavidad y partición de dominio dados . Cualquier función spline de un grado dado se puede expresar como una combinación lineal de B-splines de ese grado. Las B-splines cardinales tienen nudos que son equidistantes entre sí. Las B-splines se pueden utilizar para el ajuste de curvas y la diferenciación numérica de datos experimentales.

En el diseño asistido por computadora y los gráficos por computadora , las funciones spline se construyen como combinaciones lineales de B-splines con un conjunto de puntos de control.

Introducción

Según Gerald Farin, las B-splines fueron exploradas ya en el siglo XIX por Nikolai Lobachevsky en la Universidad de Kazán en Rusia. ^[1] El término "B-spline" fue acuñado por Isaac Jacob Schoenberg ^[2] en 1978 y es la abreviatura de spline de base. ^[3] Una función spline de orden es una función polinómica por partes de grado . Los lugares donde se encuentran las partes se conocen como nudos. La propiedad clave de las funciones spline es que ellas y sus derivadas pueden ser continuas, dependiendo de las multiplicidades de los nudos. ${\displaystyle n}$ ${\displaystyle n-1}$

Las B-splines de orden son funciones base para funciones spline del mismo orden definidas sobre los mismos nudos, lo que significa que todas las funciones spline posibles se pueden construir a partir de una combinación lineal de B-splines, y solo hay una combinación única para cada función spline. ^[4] ${\displaystyle n}$

Definición

B-spline cuadrático cardinal con vector de nudo (0, 0, 0, 1, 2, 3, 3, 3) y puntos de control (0, 0, 1, 0, 0), y su primera derivada

B-spline cúbico cardinal con vector de nudo (−2, −2, −2, −2, −1, 0, 1, 2, 2, 2, 2) y puntos de control (0, 0, 0, 6, 0, 0, 0), y su primera derivada

B-spline cuártico cardinal con vector de nudo (0, 0, 0, 0, 0, 1, 2, 3, 4, 5, 5, 5, 5, 5) y puntos de control (0, 0, 0, 0, 1, 0, 0, 0, 0), y sus derivadas primera y segunda

Una B-spline de orden es una colección de funciones polinómicas por partes de grado en una variable . Los valores de donde se unen las partes del polinomio se conocen como nudos, que se denotan y ordenan en orden no decreciente. ${\displaystyle p+1}$ ${\displaystyle B_{i,p}(t)}$ ${\displaystyle p}$ ${\displaystyle t}$ ${\displaystyle t}$ ${\displaystyle t_{0},t_{1},t_{2},\ldots ,t_{m}}$

Para una secuencia dada de nudos, existe, hasta un factor de escala, un spline único que satisface ${\displaystyle B_{i,p}(t)}$

${\displaystyle B_{i,p}(t)={\begin{cases}{\text{non-zero}}&{\text{if }}t_{i}\leq t<t_{i+p+1},\\0&{\text{otherwise}}.\end{cases}}}$

Si añadimos la restricción adicional de que

${\displaystyle \sum _{i=0}^{m-p-1}B_{i,p}(t)=1}$

Para todos los que se encuentran entre los nudos y , el factor de escala de se vuelve fijo. Los nudos que se encuentran entre (y sin incluir) y se denominan nudos internos. ${\displaystyle t}$ ${\displaystyle t_{p}}$ ${\displaystyle t_{m-p}}$ ${\displaystyle B_{i,p}(t)}$ ${\displaystyle t_{p}}$ ${\displaystyle t_{m-p}}$

Las B-splines se pueden construir mediante la fórmula de recursión de Cox-de Boor. Comenzamos con las B-splines de grado , es decir, polinomios constantes por partes. ${\displaystyle p=0}$

${\displaystyle B_{i,0}(t):={\begin{cases}1&{\text{if }}t_{i}\leq t<t_{i+1},\\0&{\text{otherwise}}.\end{cases}}}$

Los B-splines de grado superior se definen por recursión. ${\displaystyle (p+1)}$

${\displaystyle B_{i,p}(t):={\dfrac {t-t_{i}}{t_{i+p}-t_{i}}}B_{i,p-1}(t)+{\dfrac {t_{i+p+1}-t}{t_{i+p+1}-t_{i+1}}}B_{i+1,p-1}(t).}$

Propiedades

Una función B-spline es una combinación de bandas flexibles controladas por una serie de puntos denominados puntos de control, que crean curvas suaves. Estas funciones se utilizan para crear y gestionar formas y superficies complejas mediante una serie de puntos. La función B-spline y las funciones Bézier se aplican ampliamente en los métodos de optimización de formas. ^[5]

Una B-spline de orden es una función polinómica por partes de grado en una variable . Se define sobre ubicaciones , llamadas nudos o puntos de quiebre, que deben estar en orden no descendente . La B-spline contribuye solo en el rango entre el primero y el último de estos nudos y es cero en el resto del rango. Si cada nudo está separado por la misma distancia (donde ) de su predecesor, el vector de nudo y las B-splines correspondientes se denominan "uniformes" (consulte la B-spline cardinal a continuación). ${\displaystyle n}$ ${\displaystyle n-1}$ ${\displaystyle x}$ ${\displaystyle 1+n}$ ${\displaystyle t_{j}}$ ${\displaystyle t_{j}\leq t_{j+1}}$ ${\displaystyle h}$ ${\displaystyle h=t_{j+1}-t_{j}}$

Para cada intervalo de nudo finito donde no es cero, un B-spline es un polinomio de grado . Un B-spline es una función continua en los nudos. ^{[nota 1]} Cuando todos los nudos que pertenecen al B-spline son distintos, sus derivadas también son continuas hasta la derivada de grado . Si los nudos son coincidentes en un valor dado de , la continuidad del orden de la derivada se reduce en 1 por cada nudo coincidente adicional. Los B-splines pueden compartir un subconjunto de sus nudos, pero dos B-splines definidos sobre exactamente los mismos nudos son idénticos. En otras palabras, un B-spline se define de forma única por sus nudos. ${\displaystyle n-1}$ ${\displaystyle n-2}$ ${\displaystyle x}$

Se distinguen los nudos internos y los puntos finales. Los nudos internos cubren el dominio que nos interesa. Dado que una única B-spline ya se extiende sobre los nudos, se deduce que los nudos internos deben extenderse con puntos finales en cada lado, para dar soporte completo a la primera y la última B-spline, que afectan a los intervalos de los nudos internos. Los valores de los puntos finales no importan, normalmente el primer o el último nudo interno simplemente se repite. ${\displaystyle x}$ ${\displaystyle 1+n}$ ${\displaystyle n-1}$

La utilidad de las B-splines radica en el hecho de que cualquier función spline de orden en un conjunto dado de nudos puede expresarse como una combinación lineal de B-splines: ${\displaystyle n}$

${\displaystyle S_{n,\mathbf {t} }(x)=\sum _{i}\alpha _{i}B_{i,n}(x).}$

Las b-splines cumplen la función de funciones base para el espacio de funciones spline, de ahí su nombre. Esta propiedad se desprende del hecho de que todas las piezas tienen las mismas propiedades de continuidad, dentro de su rango de soporte individual, en los nudos. ^[6]

Las expresiones para las partes del polinomio se pueden derivar mediante la fórmula de recursión de Cox-de Boor ^[7]

${\displaystyle B_{i,0}(x):={\begin{cases}1&{\text{if }}t_{i}\leq x<t_{i+1},\\0&{\text{otherwise}}.\end{cases}}}$

${\displaystyle B_{i,k}(x):={\frac {x-t_{i}}{t_{i+k}-t_{i}}}B_{i,k-1}(x)+{\frac {t_{i+k+1}-x}{t_{i+k+1}-t_{i+1}}}B_{i+1,k-1}(x).}$

Es decir, es una constante por partes de uno o cero que indica en qué tramo de nudos se encuentra x (cero si se repite el tramo de nudos j ). La ecuación de recursión consta de dos partes: ${\displaystyle B_{j,0}(x)}$

${\displaystyle {\frac {x-t_{i}}{t_{i+k}-t_{i}}}}$

rampas de cero a uno a medida que x pasa de a , y ${\displaystyle t_{i}}$ ${\displaystyle t_{i+k}}$

${\displaystyle {\frac {t_{i+k+1}-x}{t_{i+k+1}-t_{i+1}}}}$

rampas de uno a cero a medida que x va de a . Las B correspondientes son cero fuera de esos rangos respectivos. Por ejemplo, es una función triangular que es cero por debajo de , rampas a uno en y de regreso a cero en y más allá de . Sin embargo, debido a que las funciones base B-spline tienen soporte local , las B-splines generalmente se calculan mediante algoritmos que no necesitan evaluar funciones base donde son cero, como el algoritmo de De Boor . ${\displaystyle t_{i+1}}$ ${\displaystyle t_{i+k+1}}$ ${\displaystyle B_{i,1}(x)}$ ${\displaystyle x=t_{i}}$ ${\displaystyle x=t_{i+1}}$ ${\displaystyle x=t_{i+2}}$

Esta relación conduce directamente al algoritmo BSPLV codificado en FORTRAN , que genera valores de los B-splines de orden n en x . ^[8] El siguiente esquema ilustra cómo cada pieza de orden n es una combinación lineal de las piezas de B-splines de orden n  − 1 a su izquierda.

${\displaystyle {\begin{matrix}&&0\\&0&\\0&&B_{i-2,2}\\&B_{i-1,1}&\\B_{i,0}&&B_{i-1,2}\\&B_{i,1}&\\0&&B_{i,2}\\&0&\\&&0\end{matrix}}}$

La aplicación de la fórmula de recursión con los nudos en da las piezas del B-spline uniforme de orden 3 ${\displaystyle (0,1,2,3)}$

${\displaystyle {\begin{aligned}B_{1}&=x^{2}/2,&0&\leq x<1,\\B_{2}&=(-2x^{2}+6x-3)/2,&1&\leq x<2,\\B_{3}&=(3-x)^{2}/2,&2&\leq x<3.\end{aligned}}}$

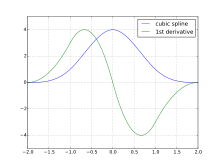
Estas piezas se muestran en el diagrama. La propiedad de continuidad de una función spline cuadrática y su primera derivada en los nudos internos se ilustran de la siguiente manera

${\displaystyle {\begin{aligned}&{\text{At }}x=1\colon \ B_{1}=B_{2}=0.5,\ {\frac {dB_{1}}{dx}}={\frac {dB_{2}}{dx}}=1.\\[6pt]&{\text{At }}x=2\colon \ B_{2}=B_{3}=0.5,\ {\frac {dB_{2}}{dx}}={\frac {dB_{3}}{dx}}=-1.\end{aligned}}}$

La segunda derivada de una B-spline de grado 2 es discontinua en los nudos:

${\displaystyle {\frac {d^{2}B_{1}}{dx^{2}}}=1,\ {\frac {d^{2}B_{2}}{dx^{2}}}=-2,\ {\frac {d^{2}B_{3}}{dx^{2}}}=1.}$

Se han propuesto variantes más rápidas del algoritmo de De Boor, pero adolecen de una estabilidad comparativamente menor. ^{[9] [10]}

B-spline cardinal

Una B-spline cardinal tiene una separación constante h entre nudos. Las B-splines cardinales para un orden n dado son simplemente copias desplazadas unas de otras. Se pueden obtener a partir de la definición más simple. ^[11]

${\displaystyle B_{i,n,t}(x)={\frac {x-t_{i}}{h}}n[0,\dots ,n](\cdot -t_{i})_{+}^{n-1}.}$

La notación "de marcador de posición" se utiliza para indicar que la n -ésima diferencia dividida de la función de las dos variables t y x debe tomarse fijando x y considerándola como una función de t únicamente. ${\displaystyle (t-x)_{+}^{n-1}}$ ${\displaystyle (t-x)_{+}^{n-1}}$

Un B-spline cardinal tiene nudos espaciados uniformemente, por lo tanto, la interpolación entre los nudos equivale a una convolución con un núcleo de suavizado.

Por ejemplo, si queremos interpolar tres valores entre los nodos B-spline ( ), podemos escribir la señal como ${\displaystyle {\textbf {b}}}$

${\displaystyle \mathbf {x} =[\mathbf {b} _{1},0,0,\mathbf {b} _{2},0,0,\mathbf {b} _{3},0,0,\dots ,\mathbf {b} _{n},0,0].}$

La convolución de la señal con una función rectangular proporciona valores B-spline interpolados de primer orden. La interpolación B-spline de segundo orden es una convolución con una función rectangular dos veces ; mediante el filtrado iterativo con una función rectangular, se obtiene una interpolación de orden superior. ${\displaystyle \mathbf {x} }$ ${\displaystyle \mathbf {h} =[1/3,1/3,1/3]}$ ${\displaystyle \mathbf {y} =\mathbf {x} *\mathbf {h} *\mathbf {h} }$

La interpolación rápida de B-spline en un dominio de muestra uniforme se puede realizar mediante filtrado de media iterativo. Alternativamente, una función rectangular es igual a sinc en el dominio de Fourier . Por lo tanto, la interpolación de spline cúbico es igual a multiplicar la señal en el dominio de Fourier por sinc ⁴ .

Véase Distribución de Irwin-Hall#Casos especiales para expresiones algebraicas para los B-splines cardinales de grado 1–4.

P-spline

El término P-spline significa "B-spline penalizado". Se refiere al uso de la representación B-spline donde los coeficientes están determinados en parte por los datos que se van a ajustar y en parte por una función de penalización adicional que tiene como objetivo imponer suavidad para evitar el sobreajuste . ^[12]

Las aproximaciones P-spline bidimensionales y multidimensionales de datos pueden utilizar el producto de división de caras de matrices para la minimización de operaciones de cálculo. ^[13]

Expresiones derivadas

La derivada de un B-spline de grado k es simplemente una función de B-splines de grado k  − 1: ^[14]

${\displaystyle {\frac {dB_{i,k}(x)}{dx}}=k\left({\frac {B_{i,k-1}(x)}{t_{i+k}-t_{i}}}-{\frac {B_{i+1,k-1}(x)}{t_{i+k+1}-t_{i+1}}}\right).}$

Esto implica que

${\displaystyle {\frac {d}{dx}}\sum _{i}\alpha _{i}B_{i,k}=\sum _{i=r-k+2}^{s-1}k{\frac {\alpha _{i}-\alpha _{i-1}}{t_{i+k}-t_{i}}}B_{i,k-1}\quad {\text{on}}\quad [t_{r},t_{s}],}$

lo que demuestra que existe una relación simple entre la derivada de una función spline y las B-splines de grado uno menor.

Momentos de B-splines univariados

Las B-splines univariadas, es decir, las B-splines donde las posiciones de los nudos se encuentran en una única dimensión, se pueden utilizar para representar funciones de densidad de probabilidad unidimensionales . Un ejemplo es una suma ponderada de funciones de base de B-spline de orden , cada una de las cuales está normalizada por área a la unidad (es decir, no se evalúa directamente utilizando el algoritmo de-Boor estándar). ${\displaystyle p(x)}$ ${\displaystyle i}$ ${\displaystyle n}$

${\displaystyle p(x)=\sum _{i}c_{i}\cdot B_{i,n,{\textbf {norm}}}(x)}$

y con restricción de constante de normalización . El k -ésimo momento bruto de un B-spline normalizado se puede escribir como el promedio de Dirichlet de Carlson ^[15] , que a su vez se puede resolver exactamente mediante una integral de contorno y una suma iterativa ^[16] como ${\displaystyle \sum _{i}c_{i}=1}$ ${\displaystyle \mu _{k}}$ ${\displaystyle B_{i,n,{\textbf {norm}}}}$ ${\displaystyle R_{k}}$

${\displaystyle \mu _{k}=R_{k}(\mathbf {m} ;\mathbf {t} )=\int _{-\infty }^{\infty }x^{k}\cdot B_{i,n,{\textbf {norm}}}(x\mid t_{1}\dots t_{j})\,dx={\frac {\Gamma (k+1)\Gamma (m)}{\Gamma (m+k)}}\cdot D_{k}(\mathbf {m} ,\mathbf {t} )}$

con

${\displaystyle D_{k}={\frac {1}{k}}\sum \limits _{u=1}^{k}\left[\left(\sum \limits _{i=1}^{j}m_{i}\cdot {t_{i}}^{u}\right)D_{k-u}\right]}$

y . Aquí, representa un vector con las posiciones de los nudos y un vector con las respectivas multiplicidades de los nudos. Por lo tanto, se puede calcular cualquier momento de una función de densidad de probabilidad representada por una suma de funciones base B-spline de manera exacta, sin recurrir a técnicas numéricas. ${\displaystyle D_{0}=1}$ ${\displaystyle \mathbf {t} }$ ${\displaystyle j}$ ${\displaystyle \mathbf {m} }$ ${\displaystyle p(x)}$

Relación con la curva Bézier compuesta/por partes

Una curva de Bézier también es una curva polinómica definible mediante una recursión a partir de curvas de grado inferior de la misma clase y codificada en términos de puntos de control, pero una diferencia clave es que todos los términos en la recursión para un segmento de curva de Bézier tienen el mismo dominio de definición (generalmente ), mientras que los soportes de los dos términos en la recursión B-spline son diferentes (los subintervalos más externos no son comunes). Esto significa que una curva de Bézier de grado dado por puntos de control consta de segmentos en su mayoría independientes, mientras que la B-spline con los mismos parámetros pasa suavemente de un subintervalo a otro. Para obtener algo comparable a partir de una curva de Bézier, se necesitaría imponer una condición de suavidad en las transiciones entre segmentos, lo que daría como resultado algún tipo de spline de Bézier (para el cual muchos puntos de control estarían determinados por el requisito de suavidad). ${\displaystyle [0,1]}$ ${\displaystyle n}$ ${\displaystyle m\gg n}$ ${\displaystyle m/n}$

Una curva de Bézier compuesta/por partes es una serie de curvas de Bézier unidas con al menos una continuidad C0 (el último punto de una curva coincide con el punto de inicio de la siguiente curva). Según la aplicación, se pueden añadir requisitos de suavidad adicionales (como la continuidad C1 o C2). ^[17] Las curvas continuas C1 tienen tangentes idénticas en el punto de quiebre (donde se encuentran las dos curvas). Las curvas continuas C2 tienen una curvatura idéntica en el punto de quiebre. ^[18]

Ajuste de curvas

Por lo general, en el ajuste de curvas , un conjunto de puntos de datos se ajusta con una curva definida por alguna función matemática. Por ejemplo, los tipos comunes de ajuste de curvas utilizan un polinomio o un conjunto de funciones exponenciales . Cuando no hay una base teórica para elegir una función de ajuste, la curva se puede ajustar con una función spline compuesta por una suma de B-splines, utilizando el método de mínimos cuadrados . ^{[19] [nota 2]} Por lo tanto, la función objetivo para la minimización de mínimos cuadrados es, para una función spline de grado k ,

${\displaystyle U=\sum _{{\text{all}}~x}\left\{W(x)\left[y(x)-\sum _{i}\alpha _{i}B_{i,k,t}(x)\right]\right\}^{2},}$

donde W ( x ) es un peso e y ( x ) es el valor de referencia en x . Los coeficientes son los parámetros que se deben determinar. Los valores de los nudos pueden ser fijos o tratados como parámetros. ${\displaystyle \alpha _{i}}$

La principal dificultad en la aplicación de este proceso es determinar el número de nudos a utilizar y dónde deben colocarse. De Boor sugiere varias estrategias para abordar este problema. Por ejemplo, el espaciado entre nudos se reduce en proporción a la curvatura (2da derivada) de los datos. ^{[ cita requerida ]} Se han publicado algunas aplicaciones. Por ejemplo, se ha investigado el uso de B-splines para ajustar curvas lorentzianas y gaussianas simples . Se han calculado funciones spline óptimas de grados 3 a 7 inclusive, basadas en arreglos simétricos de 5, 6 y 7 nudos, y se aplicó el método para suavizar y diferenciar curvas espectroscópicas. ^[20] En un estudio comparable, la versión bidimensional del filtrado de Savitzky-Golay y el método spline produjeron mejores resultados que el filtrado de promedio móvil o Chebyshev . ^[21]

Diseño asistido por ordenador y gráficos por ordenador

En las aplicaciones de diseño asistido por ordenador y gráficos por ordenador , una curva spline se representa a veces como , una curva paramétrica de algún parámetro real . En este caso, la curva se puede tratar como dos o tres funciones de coordenadas independientes , o . Las funciones de coordenadas , y son funciones spline, con un conjunto común de valores de nudo . ${\displaystyle C(t)}$ ${\displaystyle t}$ ${\displaystyle C(t)}$ ${\displaystyle (x(t),y(t))}$ ${\displaystyle (x(t),y(t),z(t))}$ ${\displaystyle x(t)}$ ${\displaystyle y(t)}$ ${\displaystyle z(t)}$ ${\displaystyle t_{1},t_{2},\ldots ,t_{n}}$

Debido a que las B-splines forman funciones base, cada una de las funciones de coordenadas se puede expresar como una suma lineal de B-splines, por lo que tenemos

${\displaystyle {\begin{aligned}X(t)&=\sum _{i}x_{i}B_{i,n}(t),\\Y(t)&=\sum _{i}y_{i}B_{i,n}(t),\\Z(t)&=\sum _{i}z_{i}B_{i,n}(t).\end{aligned}}}$

Los pesos y se pueden combinar para formar puntos en el espacio tridimensional. Estos puntos se conocen comúnmente como puntos de control. ${\displaystyle x_{i}}$ ${\displaystyle y_{i}}$ ${\displaystyle z_{i}}$ ${\displaystyle P_{i}=(x_{i},y_{i},z_{i})}$ ${\displaystyle P_{i}}$

Trabajando a la inversa, una secuencia de puntos de control, valores de nudo y orden de la B-spline definen una curva paramétrica. Esta representación de una curva por puntos de control tiene varias propiedades útiles:

1. Los puntos de control definen una curva. Si todos los puntos de control se transforman juntos de alguna manera, como por ejemplo, si se trasladan, rotan, escalan o mueven mediante alguna transformación afín, la curva correspondiente se transforma de la misma manera. ${\displaystyle P_{i}}$
2. Debido a que los B-splines no son cero solo para un número finito de intervalos de nudos, si se mueve un solo punto de control, el cambio correspondiente en la curva paramétrica está justo por encima del rango de parámetros de un pequeño número de intervalos de nudos.
3. Debido a que , y en todo momento cada , entonces la curva permanece dentro del cuadro delimitador de los puntos de control. Además, en cierto sentido, la curva sigue ampliamente los puntos de control. ${\displaystyle \sum _{i}B_{i,n}(x)=1}$ ${\displaystyle B_{i,n}(x)\geq 0}$

Una característica menos deseable es que la curva paramétrica no interpola los puntos de control. Por lo general, la curva no pasa por los puntos de control.

B-Splines cúbicos

Una curva B-spline cúbica con un parámetro normalizado se define mediante cuatro nodos (es decir, puntos de control ) , , , y . Forma un polinomio de grado 3 que se puede escribir como ${\displaystyle \mathbf {C} (t)}$ ${\displaystyle t\in [0,1]}$ ${\displaystyle {\textbf {b}}_{0}}$ ${\displaystyle {\textbf {b}}_{1}}$ ${\displaystyle {\textbf {b}}_{2}}$ ${\displaystyle {\textbf {b}}_{3}}$

${\displaystyle \mathbf {C} (t)={\frac {1}{6}}\;{\begin{bmatrix}t^{3}&t^{2}&t&1\end{bmatrix}}{\begin{bmatrix}-1&3&-3&1\\3&-6&3&0\\-3&0&3&0\\1&4&1&0\end{bmatrix}}{\begin{bmatrix}\mathbf {b} _{0}\\\mathbf {b} _{1}\\\mathbf {b} _{2}\\\mathbf {b} _{3}\end{bmatrix}}}$.

Esto corresponde a polinomios B-spline

${\displaystyle {\begin{aligned}B_{0}(t)&={\frac {1}{6}}(-t^{3}+3t^{2}-3t+1)\\B_{1}(t)&={\frac {1}{6}}(3t^{3}-6t^{2}+4)\\B_{2}(t)&={\frac {1}{6}}(-3t^{3}+3t^{2}+3t+1)\\B_{3}(t)&={\frac {1}{6}}t^{3}\end{aligned}}}$

y la curva se puede evaluar como . Desarrollando esto, podemos escribir la forma polinómica completa como se muestra a continuación ${\displaystyle \mathbf {C} (t)=\sum _{i=0}^{3}B_{i}(t)\,\mathbf {b} _{i}}$

${\displaystyle \mathbf {C} (t)={\frac {1}{6}}{\biggl (}(-\mathbf {b} _{0}+3\mathbf {b} _{1}-3\mathbf {b} _{2}+\mathbf {b} _{3})t^{3}+(3\mathbf {b} _{0}-6\mathbf {b} _{1}+3\mathbf {b} _{2})t^{2}+(-3\mathbf {b} _{0}+3\mathbf {b} _{2})t+(\mathbf {b} _{0}+4\mathbf {b} _{1}+\mathbf {b} _{2}){\biggr )}}$.

Como se trata de un polinomio cúbico, también podemos escribirlo como una curva de Bézier cúbica con puntos de control , , , y , de modo que ${\displaystyle {\textbf {P}}_{0}}$ ${\displaystyle {\textbf {P}}_{1}}$ ${\displaystyle {\textbf {P}}_{2}}$ ${\displaystyle {\textbf {P}}_{3}}$

${\displaystyle {\begin{aligned}\mathbf {P} _{0}&={\frac {1}{6}}(\mathbf {b} _{0}+4\mathbf {b} _{1}+\mathbf {b} _{2}),\\\mathbf {P} _{1}&={\frac {1}{3}}(2\mathbf {b} _{1}+\mathbf {b} _{2}),\\\mathbf {P} _{2}&={\frac {1}{3}}(\mathbf {b} _{1}+2\mathbf {b} _{2}),\\\mathbf {P} _{3}&={\frac {1}{6}}(\mathbf {b} _{1}+4\mathbf {b} _{2}+\mathbf {b} _{3}).\end{aligned}}}$

Una B-spline cúbica por partes está formada por un conjunto de nodos y cada cuatro nodos consecutivos definen una parte cúbica de la curva con la formulación anterior.

NURBS

Curva NURBS: curva polinómica definida en coordenadas homogéneas (azul) y su proyección en el plano: curva racional (roja)

En el diseño asistido por ordenador , la fabricación asistida por ordenador y los gráficos por ordenador , una potente extensión de las B-splines son las B-splines racionales no uniformes (NURBS). Las NURBS son esencialmente B-splines en coordenadas homogéneas . Al igual que las B-splines, se definen por su orden, un vector de nudo y un conjunto de puntos de control, pero a diferencia de las B-splines simples, cada punto de control tiene un peso. Cuando el peso es igual a 1, una NURBS es simplemente una B-spline y, como tal, las NURBS generalizan tanto las B-splines como las curvas y superficies de Bézier , siendo la principal diferencia la ponderación de los puntos de control que hace que las curvas NURBS sean "racionales".

Al evaluar una NURBS en varios valores de los parámetros, la curva se puede trazar a través del espacio; de la misma manera, al evaluar una superficie NURBS en varios valores de los dos parámetros, la superficie se puede representar en el espacio cartesiano.

Al igual que las B-splines, los puntos de control NURBS determinan la forma de la curva. Cada punto de la curva se calcula tomando una suma ponderada de una cantidad de puntos de control. El peso de cada punto varía según el parámetro que lo rige. Para una curva de grado d , la influencia de cualquier punto de control solo es distinta de cero en intervalos d +1 (tramos de nudos) del espacio de parámetros. Dentro de esos intervalos, el peso cambia según una función polinómica (funciones base) de grado d . En los límites de los intervalos, las funciones base tienden suavemente a cero, y la suavidad está determinada por el grado del polinomio.

El vector de nudos es una secuencia de valores de parámetros que determina dónde y cómo los puntos de control afectan la curva NURBS. La cantidad de nudos siempre es igual a la cantidad de puntos de control más el grado de la curva más uno. Cada vez que el valor del parámetro ingresa a un nuevo intervalo de nudos, se activa un nuevo punto de control, mientras que se descarta un punto de control anterior.

Una curva NURBS toma la siguiente forma: ^[22]

${\displaystyle C(u)={\frac {\sum _{i=1}^{k}N_{i,n}(u)w_{i}P_{i}}{\sum _{i=1}^{k}N_{i,n}(u)w_{i}}}}$

Aquí la notación es la siguiente: u es la variable independiente (en lugar de x ), k es el número de puntos de control, N es un B-spline (usado en lugar de B ), n es el grado del polinomio, P es un punto de control y w es un peso. El denominador es un factor normalizador que evalúa a uno si todos los pesos son uno.

Es costumbre escribir esto como

${\displaystyle C(u)=\sum _{i=1}^{k}R_{i,n}(u)P_{i}}$

En el que las funciones

${\displaystyle R_{i,n}(u)={\frac {N_{i,n}(u)w_{i}}{\sum _{j=1}^{k}N_{j,n}(u)w_{j}}}}$

se conocen como funciones de base racional.

Una superficie NURBS se obtiene como el producto tensorial de dos curvas NURBS, utilizando así dos parámetros independientes u y v (con índices i y j respectivamente): ^[23]

${\displaystyle S(u,v)=\sum _{i=1}^{k}\sum _{j=1}^{\ell }R_{i,j}(u,v)P_{i,j}}$

con

${\displaystyle R_{i,j}(u,v)={\frac {N_{i,n}(u)N_{j,m}(v)w_{i,j}}{\sum _{p=1}^{k}\sum _{q=1}^{\ell }N_{p,n}(u)N_{q,m}(v)w_{p,q}}}}$

como funciones de base racional.

Véase también

• Curva de Bézier
• Spline de caja
• Algoritmo de De Boor
• I-spline
• M-spline
• Ondícula spline
• Spline en T

Notas

1. Estrictamente hablando, las B-splines generalmente se definen como continuas hacia la izquierda.
2. de Boor proporciona rutinas FORTRAN para el ajuste de mínimos cuadrados de datos experimentales.

Referencias

1. Farin, GE (2002). Curvas y superficies para CAGD: una guía práctica . Morgan Kaufmann. pág. 119.
2. de Boor, pág. 114.
3. Gary D. Knott (2000), Interpolación de splines cúbicos . Springer. pág. 151.
4. Hartmut Prautzsch; Wolfgang Böhm; Marco Paluszny (2002). Técnicas Bézier y B-Spline . Matemáticas y Visualización. Berlín, Heidelberg: Springer Science & Business Media. pag. 63.doi : 10.1007 /978-3-662-04919-8. ISBN 978-3-540-43761-1.OCLC 851370272  .
5. Talebitooti, ​​R.; Shojaeefard, MH; Yarmohammadisatri, Sadegh (2015). "Optimización del diseño de la forma de un tanque cilíndrico utilizando curvas b-spline". Computer & Fluids . 109 : 100–112. doi :10.1016/j.compfluid.2014.12.004.
6. de Boor, pág. 113.
7. de Boor, pág. 131.
8. de Boor, pág. 134.
9. Lee, ETY (diciembre de 1982). "Una rutina de cálculo B-Spline simplificada". Computing . 29 (4): 365–371. doi :10.1007/BF02246763. S2CID  2407104.
10. Lee, ETY (1986). "Comentarios sobre algunos algoritmos B-spline". Computing . 36 (3): 229–238. doi :10.1007/BF02240069. S2CID  7003455.
11. de Boor, pág. 322.
12. Eilers, PHC y Marx, BD (1996). Suavizado flexible con B-splines y penalizaciones (con comentarios y réplica). Statistical Science 11(2): 89–121.
13. Eilers, Paul HC; Marx, Brian D. (2003). "Calibración multivariada con interacción de temperatura utilizando regresión de señal penalizada bidimensional". Quimiometría y sistemas de laboratorio inteligentes . 66 (2): 159–174. doi :10.1016/S0169-7439(03)00029-7.
14. de Boor, pág. 115.
15. Carlson, BC (1991). "B-splines, funciones hipergeométricas y promedios de Dirichlet". Revista de teoría de aproximación . 67 (3): 311–325. doi : 10.1016/0021-9045(91)90006-V .
16. Glüsenkamp, ​​T. (2018). "Tratamiento probabilístico de la incertidumbre a partir del tamaño finito de datos ponderados de Monte Carlo". EPJ Plus . 133 (6): 218. arXiv : 1712.01293 . Código Bibliográfico :2018EPJP..133..218G. doi :10.1140/epjp/i2018-12042-x. S2CID  125665629.)
17. Eugene V. Shikin; Alexander I. Plis (14 de julio de 1995). Manual sobre splines para el usuario. CRC Press. pp. 96–. ISBN 978-0-8493-9404-1.
18. Wernecke, Josie (1993). "8". The Inventor Mentor: Programación de gráficos 3D orientados a objetos con Open Inventor, versión 2 (1.ª ed.). Boston, MA, EE. UU.: Addison-Wesley Longman Publishing Co., Inc. ISBN 978-0201624953.
19. de Boor, Capítulo XIV, p. 235.
20. Gans, Peter; Gill, J. Bernard (1984). "Suavizado y diferenciación de curvas espectroscópicas mediante funciones spline". Applied Spectroscopy . 38 (3): 370–376. Bibcode :1984ApSpe..38..370G. doi :10.1366/0003702844555511. S2CID  96229316.
21. Vicsek, Maria; Neal, Sharon L.; Warner, Isiah M. (1986). "Filtrado en el dominio temporal de datos de fluorescencia bidimensional". Applied Spectroscopy . 40 (4): 542–548. Bibcode :1986ApSpe..40..542V. doi :10.1366/0003702864508773. S2CID  28705788. Archivado desde el original el 23 de junio de 2017.
22. Piegl y Tiller, capítulo 4, sec. 2
23. Piegl y Tiller, capítulo 4, sec. 4

Obras citadas

• Carl de Bor (1978). Una guía práctica de splines . Springer-Verlag. ISBN 978-3-540-90356-7.
• Piegl, Les; Tiller, Wayne (1997). El libro de NURBS (2.ª ed.). Springer. ISBN 978-3-540-61545-3.

Lectura adicional

• Richard H. Bartels; John C. Beatty; Brian A. Barsky (1987). Introducción a las splines para su uso en gráficos de computadora y modelado geométrico . Morgan Kaufmann. ISBN 978-1-55860-400-1.
• Jean Gallier (1999). Curvas y superficies en modelado geométrico: teoría y algoritmos. Morgan Kaufmann. Capítulo 6. Curvas B-Spline.Este libro está agotado y se puede conseguir gratuitamente a través del autor.
• Hartmut Prautzsch; Wolfgang Böhm; Marco Paluszny (2002). Técnicas Bézier y B-Spline . Medios de ciencia y negocios de Springer. ISBN 978-3-540-43761-1.
• David Salomon (2006). Curvas y superficies para gráficos de computadora . Springer. Capítulo 7. Aproximación B-Spline. ISBN 978-0-387-28452-1.
• Hovey, Chad (2022). Formulación e implementación en Python de geometría Bézier y B-Spline. SAND2022-7702C. (153 páginas)

Enlaces externos

• Weisstein, Eric W. "B-Spline". MathWorld .
• Ruf, Johannes. "B-splines de tercer orden en una cuadrícula no uniforme" (PDF) . Archivado desde el original (PDF) el 2013-11-06 . Consultado el 2012-05-02 .
• B-spline bivariado de numpy
• B-splines interactivos con JSXGraph
• TinySpline: biblioteca C de código abierto con enlaces para varios lenguajes
• B-Splines uniformes no racionales, modelado de curvas en el espacio 2D. Autor: Stefan G. Beck
• Editor B-Spline de Shukant Pal