En química , cristalografía y ciencia de los materiales , el número de coordinación , también llamado ligancia , de un átomo central en una molécula o cristal es el número de átomos, moléculas o iones unidos a él. El ion/molécula/átomo que rodea al ion/molécula/átomo central se denomina ligando . Este número se determina de forma algo diferente para las moléculas que para los cristales.
En el caso de las moléculas y los iones poliatómicos, el número de coordinación de un átomo se determina simplemente contando los otros átomos a los que está unido (mediante enlaces simples o múltiples). [1] Por ejemplo, [Cr(NH 3 ) 2 Cl 2 Br 2 ] − tiene como catión central a Cr 3+ , que tiene un número de coordinación de 6 y se describe como hexacoordinado . Los números de coordinación comunes son 4 , 6 y 8.

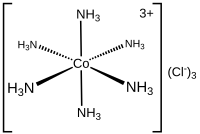

En química, el número de coordinación , definido originalmente en 1893 por Alfred Werner , es el número total de vecinos de un átomo central en una molécula o ion. [1] [3] El concepto se aplica más comúnmente a los complejos de coordinación .
El número de coordinación más común para los complejos de metales de transición del bloque d es 6. El número de coordinación no distingue la geometría de dichos complejos, es decir, octaédrico o prismático trigonal.
Para los complejos de metales de transición, los números de coordinación varían de 2 (por ejemplo, Au I en Ph 3 PAuCl) a 9 (por ejemplo, Re VII en [ReH 9 ] 2− ). Los metales en el bloque f (los lantánidos y actínidos ) pueden acomodar un número de coordinación más alto debido a sus mayores radios iónicos y la disponibilidad de más orbitales para el enlace. Los números de coordinación de 8 a 12 se observan comúnmente para los elementos del bloque f . Por ejemplo, con iones nitrato bidentados como ligandos, Ce IV y Th IV forman los iones de 12 coordenadas [Ce(NO 3 ) 6 ] 2− ( nitrato de amonio cérico ) y [Th(NO 3 ) 6 ] 2− . Cuando los ligandos circundantes son mucho más pequeños que el átomo central, pueden ser posibles números de coordinación incluso más altos. Un estudio de química computacional predijo un PbHe particularmente estable2+
15ion compuesto por un ion de plomo central coordinado con no menos de 15 átomos de helio. [4] Entre las fases de Frank-Kasper , el empaquetamiento de átomos metálicos puede dar números de coordinación de hasta 16. [5] En el extremo opuesto, el blindaje estérico puede dar lugar a números de coordinación inusualmente bajos. Un caso extremadamente raro de un metal que adopta un número de coordinación de 1 ocurre en el complejo de ariltalio(I) basado en terfenilo 2,6-Tipp 2 C 6 H 3 Tl, donde Tipp es el grupo 2,4,6-triisopropilfenilo. [6]
Los números de coordinación se vuelven ambiguos cuando se trata de ligandos polihapto. Para ligandos de electrones π como el ion ciclopentadienuro [C 5 H 5 ] − , alquenos y el ion ciclooctatetraenuro [C 8 H 8 ] 2− , el número de átomos adyacentes en el sistema de electrones π que se unen al átomo central se denomina hapticidad . [7] En el ferroceno, la hapticidad, η , de cada anión ciclopentadienuro es cinco, Fe( η 5 -C 5 H 5 ) 2 . Existen varias formas de asignar la contribución hecha al número de coordinación del átomo de hierro central por cada ligando ciclopentadienuro. La contribución podría asignarse como uno ya que hay un ligando, o como cinco ya que hay cinco átomos vecinos, o como tres ya que hay tres pares de electrones involucrados. Normalmente se toma el recuento de pares de electrones. [8]
Los números de coordinación están bien definidos para los átomos en el interior de una red cristalina : se cuentan los vecinos más cercanos en todas las direcciones. El número de vecinos de un átomo interior se denomina número de coordinación en masa . Para las superficies, el número de vecinos es más limitado, por lo que el número de coordinación de la superficie es menor que el número de coordinación en masa. A menudo, el número de coordinación de la superficie es desconocido o variable. [9] El número de coordinación de la superficie también depende de los índices de Miller de la superficie. En un cristal cúbico centrado en el cuerpo (BCC) , el número de coordinación en masa es 8, mientras que, para la superficie (100), el número de coordinación de la superficie es 4. [10]
Una forma común de determinar el número de coordinación de un átomo es mediante cristalografía de rayos X. Las técnicas relacionadas incluyen la difracción de neutrones o de electrones . [11] El número de coordinación de un átomo se puede determinar directamente contando los vecinos más cercanos.
El α-aluminio tiene una estructura cúbica regular compacta, fcc , donde cada átomo de aluminio tiene 12 vecinos más cercanos, 6 en el mismo plano y 3 arriba y abajo, y el poliedro de coordinación es un cuboctaedro . El α-hierro tiene una estructura cúbica centrada en el cuerpo donde cada átomo de hierro tiene 8 vecinos más cercanos situados en las esquinas de un cubo.

Los dos alótropos más comunes del carbono tienen diferentes números de coordinación. En el diamante , cada átomo de carbono está en el centro de un tetraedro regular formado por otros cuatro átomos de carbono; el número de coordinación es cuatro, como en el caso del metano. El grafito está formado por capas bidimensionales en las que cada carbono está unido covalentemente a otros tres carbonos; los átomos de otras capas están más alejados y no son vecinos más próximos, lo que da un número de coordinación de 3. [12]


En el caso de compuestos químicos con redes regulares, como el cloruro de sodio y el cloruro de cesio , el recuento de los vecinos más próximos proporciona una buena imagen del entorno de los iones. En el cloruro de sodio, cada ion de sodio tiene 6 iones de cloruro como vecinos más próximos (a 276 pm) en las esquinas de un octaedro y cada ion de cloruro tiene 6 átomos de sodio (también a 276 pm) en las esquinas de un octaedro. En el cloruro de cesio, cada cesio tiene 8 iones de cloruro (a 356 pm) situados en las esquinas de un cubo y cada cloruro tiene ocho iones de cesio (también a 356 pm) en las esquinas de un cubo.
En algunos compuestos, los enlaces metal-ligando pueden no estar todos a la misma distancia. Por ejemplo, en PbCl 2 , se podría decir que el número de coordinación de Pb 2+ es siete o nueve, dependiendo de qué cloruros se asignen como ligandos. Siete ligandos de cloruro tienen distancias Pb-Cl de 280-309 pm. Dos ligandos de cloruro están más distantes, con una distancia Pb-Cl de 370 pm. [13]
En algunos casos se utiliza una definición diferente de número de coordinación que incluye átomos a una distancia mayor que sus vecinos más cercanos. La definición muy amplia adoptada por la Unión Internacional de Cristalografía , IUCR, establece que el número de coordinación de un átomo en un sólido cristalino depende del modelo de enlace químico y de la forma en que se calcula el número de coordinación. [14] [15]
Algunos metales tienen estructuras irregulares. Por ejemplo, el cinc tiene una estructura hexagonal compacta distorsionada. El empaquetamiento hexagonal compacto regular de esferas predeciría que cada átomo tiene 12 vecinos más próximos y un poliedro de coordinación ortobicúpula triangular (también llamado anticuboctaedro o cuboctaedro maclado). [12] [16] En el cinc hay solo 6 vecinos más próximos a 266 pm en el mismo plano compacto con otros seis vecinos más próximos, equidistantes, tres en cada uno de los planos compactos superior e inferior a 291 pm. Se considera razonable describir el número de coordinación como 12 en lugar de 6. [15] Se pueden aplicar consideraciones similares a la estructura regular de cubo centrado en el cuerpo donde además de los 8 vecinos más próximos hay 6 más, aproximadamente un 15% más distantes, [12] y en este caso el número de coordinación se considera a menudo como 14.

Muchos compuestos químicos tienen estructuras distorsionadas. El arseniuro de níquel , NiAs, tiene una estructura en la que los átomos de níquel y arsénico están en coordenada 6. A diferencia del cloruro de sodio, donde los iones de cloruro están empaquetados de forma cúbica, los aniones de arsénico están empaquetados de forma hexagonal. Los iones de níquel están en coordenada 6 con un poliedro de coordinación octaédrica distorsionada, donde las columnas de octaedros comparten caras opuestas. Los iones de arsénico no están coordinados octaédricamente, sino que tienen un poliedro de coordinación prismático trigonal. Una consecuencia de esta disposición es que los átomos de níquel están bastante cerca unos de otros. Otros compuestos que comparten esta estructura, o una estrechamente relacionada, son algunos sulfuros de metales de transición como FeS y CoS , así como algunos intermetálicos. En el telururo de cobalto (II), CoTe, los seis átomos de telurio y dos de cobalto están todos equidistantes del átomo central de Co. [12]

Otros dos ejemplos de sustancias químicas que se encuentran con frecuencia son el Fe2O3 y el TiO2 . El Fe2O3 tiene una estructura cristalina que puede describirse como una matriz casi compacta de átomos de oxígeno con átomos de hierro que llenan dos tercios de los huecos octaédricos. Sin embargo, cada átomo de hierro tiene 3 vecinos más cercanos y otros 3 un poco más alejados. La estructura es bastante compleja, los átomos de oxígeno están coordinados con cuatro átomos de hierro y los átomos de hierro a su vez comparten vértices, aristas y caras de los octaedros distorsionados. [12] El TiO2 tiene la estructura del rutilo . Los átomos de titanio tienen 6 coordenadas, 2 átomos a 198,3 pm y 4 a 194,6 pm, en un octaedro ligeramente distorsionado. Los octaedros alrededor de los átomos de titanio comparten aristas y vértices para formar una red tridimensional. Los iones de óxido tienen 3 coordenadas en una configuración plana trigonal . [17]


El número de coordinación de sistemas con desorden no se puede definir con precisión.
El primer número de coordinación se puede definir utilizando la función de distribución radial g ( r ): [18] [19] donde r 0 es la posición más a la derecha a partir de r = 0 donde g ( r ) es aproximadamente cero, r 1 es el primer mínimo. Por lo tanto, es el área bajo el primer pico de g ( r ).
El segundo número de coordinación se define de manera similar:
Se pueden encontrar definiciones alternativas para el número de coordinación en la literatura, pero en esencia la idea principal es la misma. Una de esas definiciones es la siguiente: Denotando la posición del primer pico como r p ,
La primera capa de coordinación es la capa esférica con un radio entre r 0 y r 1 alrededor de la partícula central bajo investigación. [20] [21]