Algoritmo de Gauss-Newton

Algoritmo matemático

Ajuste de una curva ruidosa mediante un modelo de pico asimétrico con parámetros que minimizan la suma de los cuadrados de los residuos en los puntos de la cuadrícula , utilizando el algoritmo de Gauss-Newton. Arriba: Datos brutos y modelo. Abajo: Evolución de la suma normalizada de los cuadrados de los errores. ${\displaystyle f_{\beta }(x)}$ ${\displaystyle \beta }$ ${\displaystyle r_{i}(\beta )=y_{i}-f_{\beta }(x_{i})}$ ${\displaystyle x_{i}}$

El algoritmo de Gauss-Newton se utiliza para resolver problemas de mínimos cuadrados no lineales , lo que equivale a minimizar una suma de valores de funciones al cuadrado. Es una extensión del método de Newton para encontrar un mínimo de una función no lineal . Dado que una suma de cuadrados debe ser no negativa, el algoritmo puede considerarse como un método que utiliza el método de Newton para aproximar iterativamente los ceros de los componentes de la suma y, por lo tanto, minimizar la suma. En este sentido, el algoritmo también es un método eficaz para resolver sistemas de ecuaciones sobredeterminados. Tiene la ventaja de que no se requieren segundas derivadas, que pueden ser difíciles de calcular. ^[1]

Los problemas de mínimos cuadrados no lineales surgen, por ejemplo, en la regresión no lineal , donde se buscan parámetros en un modelo tales que el modelo concuerde bien con las observaciones disponibles.

El método lleva el nombre de los matemáticos Carl Friedrich Gauss e Isaac Newton , y apareció por primera vez en la obra de Gauss de 1809 Theoria motus corporum coelestium in sectionibus conicis solem ambientum . ^[2]

Descripción

Dadas funciones (a menudo llamadas residuos) de variables , el algoritmo de Gauss-Newton encuentra iterativamente el valor de que minimiza la suma de cuadrados ^[3] ${\displaystyle m}$ ${\displaystyle {\textbf {r}}=(r_{1},\ldots ,r_{m})}$ ${\displaystyle n}$ ${\displaystyle {\boldsymbol {\beta }}=(\beta _{1},\ldots \beta _{n}),}$ ${\displaystyle m\geq n,}$ ${\displaystyle \beta }$ $${\displaystyle S({\boldsymbol {\beta }})=\sum _{i=1}^{m}r_{i}({\boldsymbol {\beta }})^{2}.}$$

Partiendo de una estimación inicial del mínimo, el método avanza mediante iteraciones. ${\displaystyle {\boldsymbol {\beta }}^{(0)}}$ $${\displaystyle {\boldsymbol {\beta }}^{(s+1)}={\boldsymbol {\beta }}^{(s)}-\left(\mathbf {J_{r}} ^{\operatorname {T} }\mathbf {J_{r}} \right)^{-1}\mathbf {J_{r}} ^{\operatorname {T} }\mathbf {r} \left({\boldsymbol {\beta }}^{(s)}\right),}$$

donde, si r y β son vectores columna , las entradas de la matriz jacobiana son $${\displaystyle \left(\mathbf {J_{r}} \right)_{ij}={\frac {\partial r_{i}\left({\boldsymbol {\beta }}^{(s)}\right)}{\partial \beta _{j}}},}$$

y el símbolo denota la matriz transpuesta . ${\displaystyle ^{\operatorname {T} }}$

En cada iteración, la actualización se puede encontrar reorganizando la ecuación anterior en los dos pasos siguientes: ${\displaystyle \Delta ={\boldsymbol {\beta }}^{(s+1)}-{\boldsymbol {\beta }}^{(s)}}$

• ${\displaystyle \Delta =-\left(\mathbf {J_{r}} ^{\operatorname {T} }\mathbf {J_{r}} \right)^{-1}\mathbf {J_{r}} ^{\operatorname {T} }\mathbf {r} \left({\boldsymbol {\beta }}^{(s)}\right)}$
• ${\displaystyle \mathbf {J_{r}} ^{\operatorname {T} }\mathbf {J_{r}} \Delta =-\mathbf {J_{r}} ^{\operatorname {T} }\mathbf {r} \left({\boldsymbol {\beta }}^{(s)}\right)}$

Con las sustituciones , , y , esto se convierte en la ecuación matricial convencional de la forma , que luego puede resolverse mediante una variedad de métodos (ver Notas). ${\textstyle A=\mathbf {J_{r}} ^{\operatorname {T} }\mathbf {J_{r}} }$ ${\displaystyle \mathbf {b} =-\mathbf {J_{r}} ^{\operatorname {T} }\mathbf {r} \left({\boldsymbol {\beta }}^{(s)}\right)}$ ${\displaystyle \mathbf {x} =\Delta }$ ${\displaystyle A\mathbf {x} =\mathbf {b} }$

Si m = n , la iteración se simplifica a

$${\displaystyle {\boldsymbol {\beta }}^{(s+1)}={\boldsymbol {\beta }}^{(s)}-\left(\mathbf {J_{r}} \right)^{-1}\mathbf {r} \left({\boldsymbol {\beta }}^{(s)}\right),}$$

lo cual es una generalización directa del método de Newton en una dimensión.

En el ajuste de datos, donde el objetivo es encontrar los parámetros tales que una función de modelo dada se ajuste mejor a algunos puntos de datos , las funciones son los residuos : ${\displaystyle {\boldsymbol {\beta }}}$ ${\displaystyle \mathbf {f} (\mathbf {x} ,{\boldsymbol {\beta }})}$ ${\displaystyle (x_{i},y_{i})}$ ${\displaystyle r_{i}}$ $${\displaystyle r_{i}({\boldsymbol {\beta }})=y_{i}-f\left(x_{i},{\boldsymbol {\beta }}\right).}$$

Entonces, el método de Gauss-Newton se puede expresar en términos del jacobiano de la función como ${\displaystyle \mathbf {J_{f}} =-\mathbf {J_{r}} }$ ${\displaystyle \mathbf {f} }$ $${\displaystyle {\boldsymbol {\beta }}^{(s+1)}={\boldsymbol {\beta }}^{(s)}+\left(\mathbf {J_{f}} ^{\operatorname {T} }\mathbf {J_{f}} \right)^{-1}\mathbf {J_{f}} ^{\operatorname {T} }\mathbf {r} \left({\boldsymbol {\beta }}^{(s)}\right).}$$

Nótese que es la pseudoinversa izquierda de . ${\displaystyle \left(\mathbf {J_{f}} ^{\operatorname {T} }\mathbf {J_{f}} \right)^{-1}\mathbf {J_{f}} ^{\operatorname {T} }}$ ${\displaystyle \mathbf {J_{f}} }$

Notas

La suposición de que m ≥ n en el enunciado del algoritmo es necesaria, ya que de lo contrario la matriz no es invertible y las ecuaciones normales no se pueden resolver (al menos de forma única). ${\displaystyle \mathbf {J_{r}} ^{T}\mathbf {J_{r}} }$

El algoritmo de Gauss-Newton se puede derivar mediante la aproximación lineal del vector de funciones r _i . Utilizando el teorema de Taylor , podemos escribir en cada iteración: $${\displaystyle \mathbf {r} ({\boldsymbol {\beta }})\approx \mathbf {r} \left({\boldsymbol {\beta }}^{(s)}\right)+\mathbf {J_{r}} \left({\boldsymbol {\beta }}^{(s)}\right)\Delta }$$

con . La tarea de encontrar la minimización de la suma de los cuadrados del lado derecho; es decir, ${\displaystyle \Delta ={\boldsymbol {\beta }}-{\boldsymbol {\beta }}^{(s)}}$ ${\displaystyle \Delta }$ $${\displaystyle \min \left\|\mathbf {r} \left({\boldsymbol {\beta }}^{(s)}\right)+\mathbf {J_{r}} \left({\boldsymbol {\beta }}^{(s)}\right)\Delta \right\|_{2}^{2},}$$

es un problema de mínimos cuadrados lineal , que puede resolverse explícitamente, produciendo las ecuaciones normales en el algoritmo.

Las ecuaciones normales son n ecuaciones lineales simultáneas en los incrementos desconocidos . Pueden resolverse en un paso, utilizando la descomposición de Cholesky o, mejor, la factorización QR de . Para sistemas grandes, un método iterativo , como el método del gradiente conjugado , puede ser más eficiente. Si hay una dependencia lineal entre las columnas de J _r , las iteraciones fallarán, ya que se vuelve singular. ${\displaystyle \Delta }$ ${\displaystyle \mathbf {J_{r}} }$ ${\displaystyle \mathbf {J_{r}} ^{T}\mathbf {J_{r}} }$

Cuando es complejo se debe utilizar la forma conjugada: . ${\displaystyle \mathbf {r} }$ ${\displaystyle \mathbf {r} :\mathbb {C} ^{n}\to \mathbb {C} }$ ${\displaystyle \left({\overline {\mathbf {J_{r}} }}^{\operatorname {T} }\mathbf {J_{r}} \right)^{-1}{\overline {\mathbf {J_{r}} }}^{\operatorname {T} }}$

Ejemplo

Curva calculada obtenida con y (en azul) versus los datos observados (en rojo) ${\displaystyle {\hat {\beta }}_{1}=0.362}$ ${\displaystyle {\hat {\beta }}_{2}=0.556}$

En este ejemplo, se utilizará el algoritmo Gauss-Newton para ajustar un modelo a algunos datos minimizando la suma de los cuadrados de los errores entre los datos y las predicciones del modelo.

En un experimento de biología que estudió la relación entre la concentración de sustrato [ S ] y la velocidad de reacción en una reacción mediada por enzimas, se obtuvieron los datos de la siguiente tabla.

Se desea encontrar una curva (función modelo) de la forma $${\displaystyle {\text{rate}}={\frac {V_{\text{max}}\cdot [S]}{K_{M}+[S]}}}$$

que se ajuste mejor a los datos en el sentido de mínimos cuadrados, con los parámetros y a determinar. ${\displaystyle V_{\text{max}}}$ ${\displaystyle K_{M}}$

Denotemos por y los valores de [ S ] y tasa respectivamente, con . Sea y . Encontraremos y tales que la suma de los cuadrados de los residuos ${\displaystyle x_{i}}$ ${\displaystyle y_{i}}$ ${\displaystyle i=1,\dots ,7}$ ${\displaystyle \beta _{1}=V_{\text{max}}}$ ${\displaystyle \beta _{2}=K_{M}}$ ${\displaystyle \beta _{1}}$ ${\displaystyle \beta _{2}}$ $${\displaystyle r_{i}=y_{i}-{\frac {\beta _{1}x_{i}}{\beta _{2}+x_{i}}},\quad (i=1,\dots ,7)}$$

se minimiza.

El jacobiano del vector de residuos con respecto a las incógnitas es una matriz cuya fila -ésima tiene las entradas ${\displaystyle \mathbf {J_{r}} }$ ${\displaystyle r_{i}}$ ${\displaystyle \beta _{j}}$ ${\displaystyle 7\times 2}$ ${\displaystyle i}$ $${\displaystyle {\frac {\partial r_{i}}{\partial \beta _{1}}}=-{\frac {x_{i}}{\beta _{2}+x_{i}}};\quad {\frac {\partial r_{i}}{\partial \beta _{2}}}={\frac {\beta _{1}\cdot x_{i}}{\left(\beta _{2}+x_{i}\right)^{2}}}.}$$

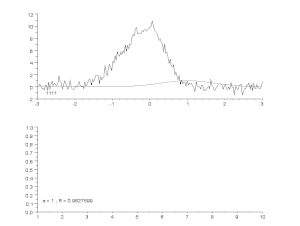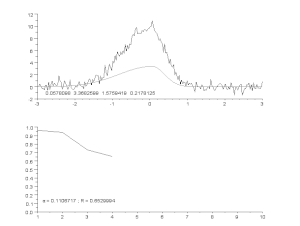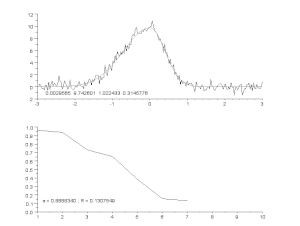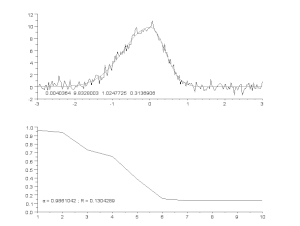
Partiendo de las estimaciones iniciales de y , tras cinco iteraciones del algoritmo de Gauss-Newton, se obtienen los valores óptimos de y . La suma de los cuadrados de los residuos disminuyó del valor inicial de 1,445 a 0,00784 tras la quinta iteración. El gráfico de la figura de la derecha muestra la curva determinada por el modelo para los parámetros óptimos con los datos observados. ${\displaystyle \beta _{1}=0.9}$ ${\displaystyle \beta _{2}=0.2}$ ${\displaystyle {\hat {\beta }}_{1}=0.362}$ ${\displaystyle {\hat {\beta }}_{2}=0.556}$

Propiedades de convergencia

Se garantiza que la iteración de Gauss-Newton convergerá hacia un punto mínimo local bajo 4 condiciones: ^[4] Las funciones son dos veces continuamente diferenciables en un conjunto convexo abierto , el jacobiano tiene rango de columna completo, la iteración inicial está cerca de , y el valor mínimo local es pequeño. La convergencia es cuadrática si . ${\displaystyle {\hat {\beta }}}$ ${\displaystyle r_{1},\ldots ,r_{m}}$ ${\displaystyle D\ni {\hat {\beta }}}$ ${\displaystyle \mathbf {J} _{\mathbf {r} }({\hat {\beta }})}$ ${\displaystyle \beta ^{(0)}}$ ${\displaystyle {\hat {\beta }}}$ ${\displaystyle |S({\hat {\beta }})|}$ ${\displaystyle |S({\hat {\beta }})|=0}$

Se puede demostrar ^[5] que el incremento Δ es una dirección de descenso para S y, si el algoritmo converge, entonces el límite es un punto estacionario de S. Sin embargo, para un valor mínimo grande , la convergencia no está garantizada, ni siquiera la convergencia local como en el método de Newton , o la convergencia bajo las condiciones habituales de Wolfe. ^[6] ${\displaystyle |S({\hat {\beta }})|}$

La tasa de convergencia del algoritmo de Gauss-Newton puede acercarse a cuadrática . ^[7] El algoritmo puede converger lentamente o no converger en absoluto si la estimación inicial está lejos del mínimo o la matriz está mal condicionada . Por ejemplo, considere el problema con ecuaciones y variable, dado por ${\displaystyle \mathbf {J_{r}^{\operatorname {T} }J_{r}} }$ ${\displaystyle m=2}$ ${\displaystyle n=1}$ $${\displaystyle {\begin{aligned}r_{1}(\beta )&=\beta +1,\\r_{2}(\beta )&=\lambda \beta ^{2}+\beta -1.\end{aligned}}}$$

El óptimo está en . (En realidad, el óptimo está en para , porque , pero .) Si , entonces el problema es de hecho lineal y el método encuentra el óptimo en una iteración. Si |λ| < 1, entonces el método converge linealmente y el error disminuye asintóticamente con un factor |λ| en cada iteración. Sin embargo, si |λ| > 1, entonces el método ni siquiera converge localmente. ^[8] ${\displaystyle \beta =0}$ ${\displaystyle \beta =-1}$ ${\displaystyle \lambda =2}$ ${\displaystyle S(0)=1^{2}+(-1)^{2}=2}$ ${\displaystyle S(-1)=0}$ ${\displaystyle \lambda =0}$

Solución de sistemas de ecuaciones sobredeterminados

La iteración de Gauss-Newton es un método eficaz para resolver sistemas de ecuaciones sobredeterminados en la forma de con y donde es la inversa de Moore-Penrose (también conocida como pseudoinversa ) de la matriz jacobiana de . Puede considerarse una extensión del método de Newton y disfruta de la misma convergencia cuadrática local ^[4] hacia soluciones regulares aisladas. $${\displaystyle \mathbf {x} ^{(k+1)}=\mathbf {x} ^{(k)}-J(\mathbf {x} ^{(k)})^{\dagger }\mathbf {f} (\mathbf {x} ^{(k)})\,,\quad k=0,1,\ldots }$$ ${\displaystyle \mathbf {f} (\mathbf {x} )=\mathbf {0} }$ $${\displaystyle \mathbf {f} (\mathbf {x} )={\begin{bmatrix}f_{1}(x_{1},\ldots ,x_{n})\\\vdots \\f_{m}(x_{1},\ldots ,x_{n})\end{bmatrix}}}$$ ${\displaystyle m>n}$ ${\displaystyle J(\mathbf {x} )^{\dagger }}$ ${\displaystyle J(\mathbf {x} )}$ ${\displaystyle \mathbf {f} (\mathbf {x} )}$

Si la solución no existe pero la iteración inicial está cerca de un punto en el que la suma de los cuadrados alcanza un mínimo local pequeño, la iteración de Gauss-Newton converge linealmente a . El punto se suele denominar solución de mínimos cuadrados del sistema sobredeterminado. ${\displaystyle \mathbf {x} ^{(0)}}$ ${\displaystyle {\hat {\mathbf {x} }}=({\hat {x}}_{1},\ldots ,{\hat {x}}_{n})}$ ${\textstyle \sum _{i=1}^{m}|f_{i}(x_{1},\ldots ,x_{n})|^{2}\equiv \|\mathbf {f} (\mathbf {x} )\|_{2}^{2}}$ ${\displaystyle {\hat {\mathbf {x} }}}$ ${\displaystyle {\hat {\mathbf {x} }}}$

Derivación del método de Newton

A continuación, se derivará el algoritmo de Gauss-Newton a partir del método de Newton para la optimización de funciones mediante una aproximación. En consecuencia, la tasa de convergencia del algoritmo de Gauss-Newton puede ser cuadrática en determinadas condiciones de regularidad. En general (en condiciones más débiles), la tasa de convergencia es lineal. ^[9]

La relación de recurrencia para el método de Newton para minimizar una función S de parámetros es ${\displaystyle {\boldsymbol {\beta }}}$ $${\displaystyle {\boldsymbol {\beta }}^{(s+1)}={\boldsymbol {\beta }}^{(s)}-\mathbf {H} ^{-1}\mathbf {g} ,}$$

donde g denota el vector de gradiente de S , y H denota la matriz hessiana de S .

Dado que , el gradiente viene dado por ${\textstyle S=\sum _{i=1}^{m}r_{i}^{2}}$ $${\displaystyle g_{j}=2\sum _{i=1}^{m}r_{i}{\frac {\partial r_{i}}{\partial \beta _{j}}}.}$$

Los elementos del hessiano se calculan diferenciando los elementos del gradiente, , con respecto a : ${\displaystyle g_{j}}$ ${\displaystyle \beta _{k}}$ $${\displaystyle H_{jk}=2\sum _{i=1}^{m}\left({\frac {\partial r_{i}}{\partial \beta _{j}}}{\frac {\partial r_{i}}{\partial \beta _{k}}}+r_{i}{\frac {\partial ^{2}r_{i}}{\partial \beta _{j}\partial \beta _{k}}}\right).}$$

El método de Gauss-Newton se obtiene ignorando los términos derivados de segundo orden (el segundo término en esta expresión). Es decir, la hessiana se aproxima mediante $${\displaystyle H_{jk}\approx 2\sum _{i=1}^{m}J_{ij}J_{ik},}$$

donde son las entradas del jacobiano J _r . Nótese que cuando el hessiano exacto se evalúa cerca de un ajuste exacto tenemos cerca de cero , por lo que el segundo término también se vuelve cerca de cero, lo que justifica la aproximación. El gradiente y el hessiano aproximado se pueden escribir en notación matricial como ${\textstyle J_{ij}={\partial r_{i}}/{\partial \beta _{j}}}$ ${\displaystyle r_{i}}$ $${\displaystyle \mathbf {g} =2{\mathbf {J} _{\mathbf {r} }}^{\operatorname {T} }\mathbf {r} ,\quad \mathbf {H} \approx 2{\mathbf {J} _{\mathbf {r} }}^{\operatorname {T} }\mathbf {J_{r}} .}$$

Estas expresiones se sustituyen en la relación de recurrencia anterior para obtener las ecuaciones operacionales. $${\displaystyle {\boldsymbol {\beta }}^{(s+1)}={\boldsymbol {\beta }}^{(s)}+\Delta ;\quad \Delta =-\left(\mathbf {J_{r}} ^{\operatorname {T} }\mathbf {J_{r}} \right)^{-1}\mathbf {J_{r}} ^{\operatorname {T} }\mathbf {r} .}$$

La convergencia del método de Gauss-Newton no está garantizada en todos los casos. La aproximación $${\displaystyle \left|r_{i}{\frac {\partial ^{2}r_{i}}{\partial \beta _{j}\partial \beta _{k}}}\right|\ll \left|{\frac {\partial r_{i}}{\partial \beta _{j}}}{\frac {\partial r_{i}}{\partial \beta _{k}}}\right|}$$

que debe cumplirse para poder ignorar los términos derivados de segundo orden puede ser válido en dos casos, para los cuales se espera convergencia: ^[10]

1. Los valores de la función son pequeños en magnitud, al menos alrededor del mínimo. ${\displaystyle r_{i}}$
2. Las funciones son sólo "levemente" no lineales, por lo que su magnitud es relativamente pequeña. ${\textstyle {\frac {\partial ^{2}r_{i}}{\partial \beta _{j}\partial \beta _{k}}}}$

Versiones mejoradas

Con el método de Gauss-Newton, la suma de los cuadrados de los residuos S no puede disminuir en cada iteración. Sin embargo, dado que Δ es una dirección descendente, a menos que sea un punto estacionario, se cumple que para todos los valores suficientemente pequeños . Por lo tanto, si se produce divergencia, una solución es emplear una fracción del vector de incremento Δ en la fórmula de actualización: ${\displaystyle S\left({\boldsymbol {\beta }}^{s}\right)}$ ${\displaystyle S\left({\boldsymbol {\beta }}^{s}+\alpha \Delta \right)<S\left({\boldsymbol {\beta }}^{s}\right)}$ ${\displaystyle \alpha >0}$ ${\displaystyle \alpha }$ $${\displaystyle {\boldsymbol {\beta }}^{s+1}={\boldsymbol {\beta }}^{s}+\alpha \Delta .}$$

En otras palabras, el vector de incremento es demasiado largo, pero aún apunta "cuesta abajo", por lo que recorrer solo una parte del camino disminuirá la función objetivo S . Se puede encontrar un valor óptimo para utilizando un algoritmo de búsqueda lineal , es decir, la magnitud de se determina encontrando el valor que minimiza S , generalmente utilizando un método de búsqueda directa en el intervalo o una búsqueda lineal de retroceso como la búsqueda lineal de Armijo . Por lo general, debe elegirse de manera que satisfaga las condiciones de Wolfe o las condiciones de Goldstein . ^[11] ${\displaystyle \alpha }$ ${\displaystyle \alpha }$ ${\displaystyle 0<\alpha <1}$ ${\displaystyle \alpha }$

En los casos en que la dirección del vector de desplazamiento es tal que la fracción óptima α es cercana a cero, un método alternativo para manejar la divergencia es el uso del algoritmo de Levenberg-Marquardt , un método de región de confianza . ^[3] Las ecuaciones normales se modifican de tal manera que el vector de incremento se rota hacia la dirección de descenso más pronunciado , $${\displaystyle \left(\mathbf {J^{\operatorname {T} }J+\lambda D} \right)\Delta =-\mathbf {J} ^{\operatorname {T} }\mathbf {r} ,}$$

donde D es una matriz diagonal positiva. Nótese que cuando D es la matriz identidad I y , entonces , por lo tanto la dirección de Δ se aproxima a la dirección del gradiente negativo . ${\displaystyle \lambda \to +\infty }$ ${\displaystyle \lambda \Delta =\lambda \left(\mathbf {J^{\operatorname {T} }J} +\lambda \mathbf {I} \right)^{-1}\left(-\mathbf {J} ^{\operatorname {T} }\mathbf {r} \right)=\left(\mathbf {I} -\mathbf {J^{\operatorname {T} }J} /\lambda +\cdots \right)\left(-\mathbf {J} ^{\operatorname {T} }\mathbf {r} \right)\to -\mathbf {J} ^{\operatorname {T} }\mathbf {r} }$ ${\displaystyle -\mathbf {J} ^{\operatorname {T} }\mathbf {r} }$

El llamado parámetro de Marquardt también puede optimizarse mediante una búsqueda lineal, pero esto es ineficiente, ya que el vector de desplazamiento debe recalcularse cada vez que se modifica. Una estrategia más eficiente es la siguiente: cuando se produce una divergencia, se aumenta el parámetro de Marquardt hasta que se produzca una disminución de S . A continuación, se conserva el valor de una iteración a la siguiente, pero se reduce si es posible hasta que se alcanza un valor de corte, cuando el parámetro de Marquardt puede establecerse en cero; la minimización de S se convierte entonces en una minimización estándar de Gauss-Newton. ${\displaystyle \lambda }$ ${\displaystyle \lambda }$

Optimización a gran escala

Para la optimización a gran escala, el método de Gauss-Newton es de especial interés porque a menudo (aunque ciertamente no siempre) es cierto que la matriz es más dispersa que la hessiana aproximada . En tales casos, el cálculo del paso en sí mismo normalmente deberá realizarse con un método iterativo aproximado apropiado para problemas grandes y dispersos, como el método del gradiente conjugado . ${\displaystyle \mathbf {J} _{\mathbf {r} }}$ ${\displaystyle \mathbf {J} _{\mathbf {r} }^{\operatorname {T} }\mathbf {J_{r}} }$

Para que este tipo de enfoque funcione, se necesita al menos un método eficiente para calcular el producto. $${\displaystyle {\mathbf {J} _{\mathbf {r} }}^{\operatorname {T} }\mathbf {J_{r}} \mathbf {p} }$$

para algún vector p . Con el almacenamiento de matrices dispersas , en general es práctico almacenar las filas de en forma comprimida (por ejemplo, sin entradas cero), lo que hace que un cálculo directo del producto anterior sea complicado debido a la transposición. Sin embargo, si se define c _i como la fila i de la matriz , se cumple la siguiente relación simple: ${\displaystyle \mathbf {J} _{\mathbf {r} }}$ ${\displaystyle \mathbf {J} _{\mathbf {r} }}$ $${\displaystyle {\mathbf {J} _{\mathbf {r} }}^{\operatorname {T} }\mathbf {J_{r}} \mathbf {p} =\sum _{i}\mathbf {c} _{i}\left(\mathbf {c} _{i}\cdot \mathbf {p} \right),}$$

de modo que cada fila contribuye de manera aditiva e independiente al producto. Además de respetar una estructura de almacenamiento dispersa práctica, esta expresión es adecuada para cálculos paralelos . Nótese que cada fila c _i es el gradiente del residuo correspondiente r _i ; con esto en mente, la fórmula anterior enfatiza el hecho de que los residuos contribuyen al problema independientemente unos de otros.

Algoritmos relacionados

En un método cuasi-Newton , como el de Davidon, Fletcher y Powell o el de Broyden–Fletcher–Goldfarb–Shanno ( método BFGS ), se construye numéricamente una estimación del hessiano completo utilizando solo las primeras derivadas, de modo que después de n ciclos de refinamiento, el método se aproxima mucho al método de Newton en rendimiento. Tenga en cuenta que los métodos cuasi-Newton pueden minimizar funciones generales de valor real, mientras que Gauss–Newton, Levenberg–Marquardt, etc. se ajustan solo a problemas de mínimos cuadrados no lineales. ${\textstyle {\frac {\partial ^{2}S}{\partial \beta _{j}\partial \beta _{k}}}}$ ${\textstyle {\frac {\partial r_{i}}{\partial \beta _{j}}}}$

Otro método para resolver problemas de minimización utilizando solo las primeras derivadas es el descenso de gradiente . Sin embargo, este método no tiene en cuenta las segundas derivadas ni siquiera de forma aproximada. En consecuencia, es altamente ineficiente para muchas funciones, especialmente si los parámetros tienen interacciones fuertes.

Ejemplos de implementación

Julia

La siguiente implementación en Julia proporciona un método que utiliza un jacobiano proporcionado y otro cálculo con diferenciación automática .

"""  gaussnewton(r,J,β₀,máximo,tol)Realice la optimización de Gauss-Newton para minimizar la función residual `r` con el jacobiano `J` comenzando desde `β₀`. El algoritmo termina cuando la norma del paso es menor que `tol` o después de iteraciones de `maxiter`. " " " function gaussnewton ( r , J , β₀ , maxiter , tol ) β = copy ( β₀ ) for_in1 : maxiterJβ = J ( β ) ; Δ = - ( Jβ ' * Jβ ) \ ( Jβ ' * r ( β ) ) β + = Δifsqrt ( sum ( abs2 , Δ ) ) < tolbreakendend returnβend                             Importe AbstractDifferentiation como AD , Zygote backend = AD . ZygoteBackend () # hay otros backends disponibles       """  gaussnewton(r,β₀,máximo,tol)Realizar la optimización de Gauss-Newton para minimizar la función residual `r` comenzando desde `β₀`. El jacobiano relevante se calcula utilizando la diferenciación automática. El algoritmo termina cuando la norma del paso es menor que `tol` o después de iteraciones `maxiter`. """ function gaussnewton ( r , β₀ , maxiter , tol ) β = copy ( β₀ ) for _ in 1 : maxiter rβ , Jβ = AD . value_and_jacobian ( backend , r , β ) Δ = - ( Jβ [ 1 ] '* Jβ [ 1 ]) \ ( Jβ [ 1 ] '* rβ ) β += Δ if sqrt ( sum ( abs2 , Δ )) < tol break end end return β end                              

Notas

1. Mittelhammer, Ron C.; Miller, Douglas J.; Judge, George G. (2000). Fundamentos econométricos. Cambridge: Cambridge University Press. págs. 197-198. ISBN 0-521-62394-4.
2. Floudas, Christodoulos A. ; Pardalos, Panos M. (2008). Enciclopedia de optimización . Springer. pág. 1130. ISBN 9780387747583.
3. Björck (1996)
4. JE Dennis, Jr. y RB Schnabel (1983). Métodos numéricos para optimización sin restricciones y ecuaciones no lineales . Reproducción de SIAM 1996 de la edición de Prentice-Hall de 1983. pág. 222.
5. Björck (1996), pág. 260.
6. Mascarenhas (2013), "La divergencia de los métodos BFGS y Gauss Newton", Programación matemática , 147 (1): 253–276, arXiv : 1309.7922 , doi :10.1007/s10107-013-0720-6, S2CID  14700106
7. Björck (1996), pág. 341, 342.
8. Fletcher (1987), pág. 113.
9. "Copia archivada" (PDF) . Archivado desde el original (PDF) el 4 de agosto de 2016. Consultado el 25 de abril de 2014 .{{cite web}}: CS1 maint: archived copy as title (link)
10. Nocedal (1999), pág. 259.
11. Nocedal, Jorge. (1999). Optimización numérica . Wright, Stephen J., 1960-. Nueva York: Springer. ISBN 0387227423.OCLC 54849297  .

Referencias

• Björck, A. (1996). Métodos numéricos para problemas de mínimos cuadrados . SIAM, Filadelfia. ISBN 0-89871-360-9.
• Fletcher, Roger (1987). Métodos prácticos de optimización (2.ª ed.). Nueva York: John Wiley & Sons . ISBN 978-0-471-91547-8..
• Nocedal, Jorge; Wright, Stephen (1999). Optimización numérica . Nueva York: Springer. ISBN 0-387-98793-2.

Enlaces externos

• Probabilidad, estadística y estimación El algoritmo se detalla y se aplica al experimento de biología discutido como ejemplo en este artículo (página 84 con las incertidumbres sobre los valores estimados).

Implementaciones

• Artelys Knitro es un solucionador no lineal con una implementación del método Gauss-Newton. Está escrito en C y tiene interfaces con C++/C#/Java/Python/MATLAB/R.