En matemáticas , E 7 es el nombre de varios grupos de Lie estrechamente relacionados , grupos algebraicos lineales o sus álgebras de Lie e 7 , todos los cuales tienen dimensión 133; la misma notación E 7 se utiliza para la red de raíces correspondiente , que tiene rango 7. La designación E 7 proviene de la clasificación de Cartan-Killing de las álgebras de Lie simples complejas , que se dividen en cuatro series infinitas etiquetadas A n , B n , C n , D n , y cinco casos excepcionales etiquetados E 6 , E 7 , E 8 , F 4 y G 2 . El álgebra E 7 es, por tanto, uno de los cinco casos excepcionales.
El grupo fundamental de la forma compleja (adjunta), la forma real compacta o cualquier versión algebraica de E 7 es el grupo cíclico Z /2 Z , y su grupo de automorfismos externo es el grupo trivial . La dimensión de su representación fundamental es 56.
Existe un álgebra de Lie compleja única de tipo E 7 , correspondiente a un grupo complejo de dimensión compleja 133. El grupo de Lie adjunto complejo E 7 de dimensión compleja 133 puede considerarse como un grupo de Lie real simple de dimensión real 266. Este tiene un grupo fundamental Z /2 Z , tiene un subgrupo compacto máximo en la forma compacta (ver más abajo) de E 7 , y tiene un grupo de automorfismo externo de orden 2 generado por conjugación compleja.
Además del grupo de Lie complejo de tipo E 7 , existen cuatro formas reales del álgebra de Lie, y correspondientemente cuatro formas reales del grupo con centro trivial (todas las cuales tienen una doble cubierta algebraica, y tres de las cuales tienen cubiertas no algebraicas adicionales, dando lugar a formas reales adicionales), todas de dimensión real 133, como sigue:
Para obtener una lista completa de formas reales de álgebras de Lie simples, consulte la lista de grupos de Lie simples .
La forma real compacta de E 7 es el grupo de isometría del espacio simétrico compacto excepcional de Riemann de 64 dimensiones EVI (en la clasificación de Cartan ). Se le conoce informalmente como el " plano proyectivo cuateroctoniónico " porque se puede construir usando un álgebra que es el producto tensorial de los cuaterniones y los octoniones , y también se le conoce como plano proyectivo de Rosenfeld , aunque no obedece a los axiomas habituales de un plano proyectivo. Esto se puede ver sistemáticamente usando una construcción conocida como el cuadrado mágico , debido a Hans Freudenthal y Jacques Tits .
La construcción de Tits-Koecher produce formas del álgebra de Lie E 7 a partir de las álgebras de Albert , álgebras de Jordan excepcionales de 27 dimensiones .
Mediante una base de Chevalley para el álgebra de Lie, se puede definir E 7 como un grupo algebraico lineal sobre los números enteros y, en consecuencia, sobre cualquier anillo conmutativo y en particular sobre cualquier cuerpo: esto define la llamada forma adjunta dividida (a veces también conocida como "destorcida") de E 7 . Sobre un cuerpo algebraicamente cerrado, esta y su doble recubrimiento son las únicas formas; sin embargo, sobre otros cuerpos, a menudo hay muchas otras formas, o "torsiones" de E 7 , que se clasifican en el marco general de la cohomología de Galois (sobre un cuerpo perfecto k ) por el conjunto H 1 ( k , Aut(E 7 )) que, debido a que el diagrama de Dynkin de E 7 (ver más abajo) no tiene automorfismos, coincide con H 1 ( k , E 7, ad ). [1]
En el cuerpo de los números reales, las componentes reales de la identidad de estas formas algebraicamente retorcidas de E 7 coinciden con los tres grupos de Lie reales mencionados anteriormente, pero con una sutileza respecto al grupo fundamental: todas las formas adjuntas de E 7 tienen grupo fundamental Z /2 Z en el sentido de la geometría algebraica, lo que significa que admiten exactamente una doble cobertura; las demás formas no compactas del grupo de Lie real de E 7 no son, por tanto, algebraicas y no admiten representaciones fieles de dimensión finita.
Sobre cuerpos finitos, el teorema de Lang-Steinberg implica que H 1 ( k , E 7 ) = 0, lo que significa que E 7 no tiene formas retorcidas: ver más abajo.
El diagrama de Dynkin para E 7 está dado por
.
Aunque las raíces abarcan un espacio de siete dimensiones, es más simétrico y conveniente representarlas como vectores que se encuentran en un subespacio de siete dimensiones de un espacio vectorial de ocho dimensiones.
Las raíces son todas las permutaciones 8×7 de (1,−1,0,0,0,0,0,0) y todas las permutaciones de ( 1/2 , 1/2 , 1/2 , 1/2 ,− 1/2 ,− 1/2 ,− 1/2 ,− 1/2 )
Tenga en cuenta que el subespacio de siete dimensiones es el subespacio donde la suma de las ocho coordenadas es cero. Hay 126 raíces.
Las raíces simples son
Se enumeran de modo que sus nodos correspondientes en el diagrama de Dynkin estén ordenados de izquierda a derecha (en el diagrama mostrado arriba) con el nodo lateral en último lugar.
Una descripción alternativa (de 7 dimensiones) del sistema de raíces, que es útil al considerar E 7 × SU(2) como un subgrupo de E 8 , es la siguiente:
Todas las permutaciones de (±1,±1,0,0,0,0,0) conservando el cero en la última entrada, todas las raíces siguientes con un número par de + 1/2
y las dos raíces siguientes
Por lo tanto, los generadores constan de una subálgebra so (12) de 66 dimensiones , así como de 64 generadores que se transforman como dos espinores de Weyl autoconjugados de espín (12) de quiralidad opuesta, y su generador de quiralidad, y otros dos generadores de quiralidades .
Dada la matriz E 7 de Cartan (abajo) y un ordenamiento de nodos del diagrama de Dynkin de:
El grupo de Weyl de E 7 es de orden 2903040: es el producto directo del grupo cíclico de orden 2 y el único grupo simple de orden 1451520 (que puede describirse como PSp 6 (2) o PSΩ 7 (2)). [2]
E 7 tiene una subálgebra SU(8), como es evidente al observar que en la descripción de 8 dimensiones del sistema de raíces, el primer grupo de raíces es idéntico a las raíces de SU(8) (con la misma subálgebra de Cartan que en E 7 ).
Además de la representación adjunta de 133 dimensiones, existe una representación "vectorial" de 56 dimensiones , que se encuentra en la representación adjunta E 8 .
Los caracteres de las representaciones de dimensión finita de las álgebras de Lie reales y complejas y de los grupos de Lie están dados por la fórmula de caracteres de Weyl . Las dimensiones de las representaciones irreducibles más pequeñas son (secuencia A121736 en la OEIS ):
Los términos subrayados en la secuencia anterior son las dimensiones de aquellas representaciones irreducibles que posee la forma adjunta de E 7 (equivalentemente, aquellas cuyos pesos pertenecen a la red raíz de E 7 ), mientras que la secuencia completa da las dimensiones de las representaciones irreducibles de la forma simplemente conexa de E 7 . Existen representaciones irreducibles no isomorfas de dimensiones 1903725824, 16349520330, etc.
Las representaciones fundamentales son aquellas con dimensiones 133, 8645, 365750, 27664, 1539, 56 y 912 (correspondientes a los siete nodos del diagrama de Dynkin en el orden elegido para la matriz de Cartan anterior, es decir, los nodos se leen primero en la cadena de seis nodos, y el último nodo se conecta al tercero).
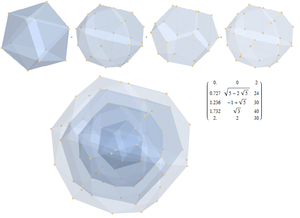
A la derecha se muestran las incrustaciones de los subgrupos máximos de E 7 hasta la dimensión 133.
E 7 es el grupo de automorfismos del siguiente par de polinomios en 56 variables no conmutativas. Dividimos las variables en dos grupos de 28, ( p , P ) y ( q , Q ) donde p y q son variables reales y P y Q son matrices hermíticas octoniónicas de 3×3 . Entonces el primer invariante es el invariante simpléctico de Sp(56, R ):
El segundo invariante más complicado es un polinomio cuártico simétrico :
Donde y el operador de círculo binario se define mediante .
Un invariante polinomial cuártico alternativo construido por Cartan utiliza dos matrices antisimétricas de 8x8, cada una con 28 componentes.
Los puntos sobre un cuerpo finito con q elementos del grupo algebraico (dividido) E 7 (ver arriba), ya sea de forma adjunta (sin centro) o simplemente conexa (su cobertura universal algebraica), dan un grupo de Chevalley finito . Este está estrechamente relacionado con el grupo escrito E 7 ( q ), sin embargo, hay ambigüedad en esta notación, que puede significar varias cosas:
Desde la perspectiva de los grupos finitos, la relación entre estos tres grupos, que es bastante análoga a la que existe entre SL( n , q ), PGL( n , q ) y PSL( n , q ), se puede resumir de la siguiente manera: E 7 ( q ) es simple para cualquier q , E 7,sc ( q ) es su cubierta de Schur , y E 7,ad ( q ) se encuentra en su grupo de automorfismos; además, cuando q es una potencia de 2, los tres coinciden, y en caso contrario (cuando q es impar), el multiplicador de Schur de E 7 ( q ) es 2 y E 7 ( q ) es de índice 2 en E 7,ad ( q ), lo que explica por qué E 7,sc ( q ) y E 7,ad ( q ) a menudo se escriben como 2·E 7 ( q ) y E 7 ( q )·2. Desde la perspectiva del grupo algebraico, es menos común que E 7 ( q ) se refiera al grupo simple finito, porque este último no es de manera natural el conjunto de puntos de un grupo algebraico sobre F q a diferencia de E 7,sc ( q ) y E 7,ad ( q ).
Como se mencionó anteriormente, E 7 ( q ) es simple para cualquier q , [3] [4] y constituye una de las familias infinitas abordadas por la clasificación de grupos finitos simples . Su número de elementos viene dado por la fórmula (secuencia A008870 en la OEIS ):
El orden de E 7,sc ( q ) o E 7,ad ( q ) (ambos son iguales) se puede obtener eliminando el factor divisor gcd(2, q −1) (secuencia A008869 en la OEIS ). El multiplicador de Schur de E 7 ( q ) es gcd(2, q −1), y su grupo de automorfismos externos es el producto del grupo de automorfismos diagonales Z /gcd(2, q −1) Z (dado por la acción de E 7,ad ( q )) y el grupo de automorfismos de cuerpo (es decir, cíclico de orden f si q = p f donde p es primo).
La supergravedad N = 8 en cuatro dimensiones, que es una reducción dimensional de la supergravedad de once dimensiones , admite una simetría global bosónica E 7 y una simetría local bosónica SU(8) . Los fermiones están en representaciones de SU(8), los campos de calibración están en una representación de E 7 y los escalares están en una representación de ambos (los gravitones son singletes con respecto a ambos). Los estados físicos están en representaciones de la clase lateral E 7 / SU(8) .
En la teoría de cuerdas , E 7 aparece como parte del grupo de calibración de una de las versiones (inestables y no supersimétricas ) de la cuerda heterótica . También puede aparecer en el grupo de calibración ininterrumpido E 8 × E 7 en compactificaciones hexadimensionales de la teoría de cuerdas heterótica, por ejemplo en la superficie cuatridimensional K3 .
![{\displaystyle C_{1}=pq-qp+Tr[PQ]-Tr[QP]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7710b7d259b59a9a6a8d8b18fcd632af7054eb6)
![{\displaystyle C_{2}=(pq+Tr[P\circ Q])^{2}+pTr[Q\circ {\tilde {Q}}]+qTr[P\circ {\tilde {P}} ]+Tr[{\tilde {P}}\circ {\tilde {Q}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8e3fd1152c0065a4edbd173f1ddaf8b25964bd4)
![{\displaystyle C_{2}=Tr[(XY)^{2}]-{\dfrac {1}{4}}Tr[XY]^{2}+{\frac {1}{96}}\epsilon _{ijklmnop}\left(X^{ij}X^{kl}X^{mn}X^{op}+Y^{ij}Y^{kl}Y^{mn}Y^{op}\right )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6282baf57eda5d68498c5eb85830709fa9484ee9)
