Espacio de color CIE 1931

En 1931, la Comisión Internacional de Iluminación (CIE) publicó los espacios de color CIE 1931 que definen la relación entre el espectro visible y la sensación visual de colores específicos por la visión del color humana . ^[1]^[2] Los espacios de color CIE son modelos matemáticos que crean un "observador estándar", que intenta predecir la percepción de tonos únicos de color. Estos espacios de color son herramientas esenciales que proporcionan la base para medir el color para la industria, incluidas las tintas, los tintes y las pinturas, la iluminación, las imágenes en color, etc. Los espacios de color CIE contribuyeron al desarrollo de la televisión en color, la creación de instrumentos para mantener un color consistente en los procesos de fabricación y otros métodos de gestión del color .

Las iniciales CIE provienen del nombre francés "Commission Internationale de l'éclairage" , que ha mantenido y desarrollado muchos de los estándares que se usan hoy en día en relación con la colorimetría . Los espacios de color CIE se crearon utilizando datos de una serie de experimentos, donde los sujetos de prueba humanos ajustaron los colores primarios rojo, verde y azul para encontrar una coincidencia visual con un segundo color puro. Los experimentos originales fueron realizados a mediados de la década de 1920 por William David Wright utilizando diez observadores ^[3] y John Guild utilizando siete observadores. ^[4] Los resultados experimentales se combinaron, creando el espacio de color CIE RGB. El espacio de color CIE XYZ se derivó de CIE RGB en un esfuerzo por simplificar las matemáticas.

El espacio de color CIE 1931 XYZ todavía se utiliza ampliamente, aunque no es uniforme desde el punto de vista perceptual en relación con la visión humana. En 1976, la CIE publicó los espacios de color CIELUV y CIELAB , que se derivan de XYZ y tienen como objetivo proporcionar predicciones más uniformes en relación con la percepción humana.

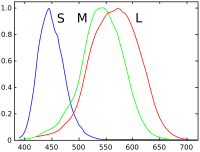
Antecedentes: el ojo humano y los valores triestímulo

El ojo humano con visión normal tiene tres tipos de células cónicas que detectan la luz, con picos de sensibilidad espectral en longitudes de onda cortas ("S", 420 nm – 440 nm ), medias ("M", 530 nm – 540 nm ) y largas ("L", 560 nm – 580 nm ). Estas células cónicas son la base de la percepción humana del color en condiciones de luminosidad media y alta; en condiciones de luz muy tenue, la visión del color disminuye y los receptores monocromáticos de "visión nocturna" de baja luminosidad, denominados " células bastón ", se vuelven efectivos. De este modo, tres parámetros correspondientes a los niveles de estímulo de las tres clases de células cónicas describen en principio cualquier sensación humana del color. Ponderando un espectro de potencia luminosa total por las sensibilidades espectrales individuales de las tres clases de células cónicas se obtienen tres valores efectivos de estímulo ; estos tres valores componen una especificación triestímulo del color objetivo del espectro de luz. Los tres parámetros, denominados "S", "M" y "L", se indican utilizando un espacio tridimensional denominado " espacio de color LMS ", que es uno de los muchos espacios de color ideados para cuantificar la visión humana del color .

Un espacio de color asigna una gama de colores producidos físicamente a partir de luz mezclada, pigmentos , etc. a una descripción objetiva de las sensaciones de color registradas en el ojo humano, típicamente en términos de valores triestímulo, pero no por lo general en el espacio de color LMS definido por las sensibilidades espectrales de las células del cono . Los valores triestímulo asociados con un espacio de color pueden conceptualizarse como cantidades de tres colores primarios en un modelo de color aditivo tricromático . En algunos espacios de color, incluidos los espacios LMS y XYZ, los colores primarios utilizados no son colores reales en el sentido de que no se pueden generar en ningún espectro de luz.

El espacio de color CIE XYZ abarca todas las sensaciones de color que son visibles para una persona con una vista promedio. Es por eso que los valores triestímulo CIE XYZ son una representación del color invariante del dispositivo. ^[5] Sirve como una referencia estándar con respecto a la cual se definen muchos otros espacios de color. Un conjunto de funciones de coincidencia de color, como las curvas de sensibilidad espectral del espacio de color LMS , pero no restringidas a sensibilidades no negativas, asocia espectros de luz producidos físicamente con valores triestímulo específicos.

Consideremos dos fuentes de luz compuestas por diferentes mezclas de distintas longitudes de onda. Dichas fuentes de luz pueden parecer del mismo color; este efecto se denomina " metamerismo ". Dichas fuentes de luz tienen el mismo color aparente para un observador cuando producen los mismos valores triestímulo, independientemente de las distribuciones de potencia espectral de las fuentes.

La mayoría de las longitudes de onda estimulan dos o los tres tipos de células cónicas porque las curvas de sensibilidad espectral de los tres tipos se superponen. Por lo tanto, ciertos valores triestímulo son físicamente imposibles: por ejemplo, los valores triestímulo LMS que no son cero para el componente M y cero para los componentes L y S. Además, los colores espectrales puros implicarían, en cualquier espacio de color aditivo tricromático normal, por ejemplo, los espacios de color RGB , valores negativos para al menos uno de los tres primarios porque la cromaticidad estaría fuera del triángulo de color definido por los colores primarios. Para evitar estos valores RGB negativos y tener un componente que describa el brillo percibido , se formularon colores primarios "imaginarios" y las funciones de coincidencia de color correspondientes. El espacio de color CIE 1931 define los valores triestímulo resultantes, en los que se denotan por "X", "Y" y "Z". ^[6] En el espacio XYZ, todas las combinaciones de coordenadas no negativas son significativas, pero muchas, como las ubicaciones primarias [1, 0, 0], [0, 1, 0] y [0, 0, 1], corresponden a colores imaginarios fuera del espacio de posibles coordenadas LMS; los colores imaginarios no corresponden a ninguna distribución espectral de longitudes de onda y, por lo tanto, no tienen realidad física.

Significado deincógnita,YyO

En el modelo CIE 1931, Y es la luminancia , Z es casi igual al azul (de CIE RGB) y X es una mezcla de las tres curvas CIE RGB elegidas como no negativas (consulte § Definición del espacio de color CIE XYZ). Establecer Y como luminancia tiene el resultado útil de que para cualquier valor de Y dado , el plano XZ contendrá todas las cromaticidades posibles en esa luminancia.

La unidad de los valores triestímulo $X$ , $Y$ y $Z$ se suele elegir de forma arbitraria, de modo que $Y = 1$ o $Y = 100$ sea el blanco más brillante que admita una pantalla en color. En este caso, el valor Y se conoce como luminancia relativa . Los valores de punto blanco correspondientes para $X$ y $Z$ se pueden inferir utilizando los iluminantes estándar .

Dado que los valores XYZ se definieron mucho antes de la caracterización de las células de los conos en la década de 1950 (por Ragnar Granit ), ^[7] el significado fisiológico de estos valores se conoce solo mucho más tarde. La matriz de Hunt-Pointer-Estevez de la década de 1980 relaciona XYZ con LMS. ^[8] Cuando se invierte, muestra cómo las tres respuestas de los conos se suman para formar funciones XYZ:

{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}=\left[{\begin{aligned}1&.910\,20\!\!&\!\!-1&.112\,12\!\!&\!\!0&.201\,91\\0&.370\,95\!\!&\!\!0&.629\,05\!\!&\!\!0&\\0&\!\!&\!\!&\!\!0&\!\!&\!\!1&.000\,00\end{aligned}}\right]{\begin{bmatrix}L\\M\\S\end{bmatrix}}_{\rm {HPE}}

En otras palabras, el valor Z se compone únicamente de la respuesta del cono S, el valor Y es una mezcla de las respuestas L y M, y el valor X es una mezcla de los tres. Este hecho hace que los valores XYZ sean análogos, pero diferentes, a las respuestas del cono LMS del ojo humano.

Observador estándar CIE

Debido a la distribución de los conos en el ojo, los valores triestímulo dependen del campo de visión del observador . Para eliminar esta variable, la CIE definió una función de mapeo de color llamada observador estándar (colorimétrico) , para representar la respuesta cromática de un humano promedio dentro de un arco de 2° dentro de la fóvea . Este ángulo se eligió debido a la creencia de que los conos sensibles al color residían dentro de un arco de 2° de la fóvea. Por lo tanto, la función CIE 1931 Standard Observer también se conoce como CIE 1931 2° Standard Observer . Una alternativa más moderna pero menos utilizada es el CIE 1964 10° Standard Observer , que se deriva del trabajo de Stiles y Burch, ^[9] y Speranskaya. ^[10]

Para los experimentos de 10°, se instruyó a los observadores para que ignoraran el punto central de 2°. Se recomienda la función de Observador Estándar Suplementario de 1964 cuando se trabaja con un campo de visión de más de 4° aproximadamente. Ambas funciones de observador estándar están discretizadas en intervalos de longitud de onda de 5 nm desde 380 nm a 780 nm y distribuidas por la CIE . ^[11] Todos los valores correspondientes se han calculado a partir de datos obtenidos experimentalmente utilizando interpolación . El observador estándar se caracteriza por tres funciones de coincidencia de color .

También hay un conjunto de datos de intervalo de 1 nm de CIE 1931 y CIE 1964 proporcionado por Wyszecki 1982. ^[12] Una publicación de CIE en 1986 también parece tener un conjunto de datos de 1 nm, probablemente utilizando los mismos datos. ^[13] Al igual que el conjunto de datos regular de 5 nm , este conjunto de datos también se deriva de la interpolación.

A continuación se presenta la derivación del observador estándar CIE a partir de experimentos de correspondencia de colores, después de la descripción del espacio RGB CIE.

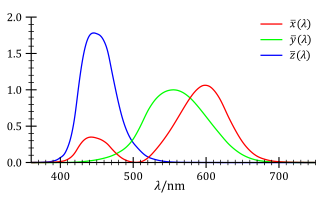
Funciones de combinación de colores

Las funciones de correspondencia de color de la CIE y son la descripción numérica de la respuesta cromática del observador (descrita anteriormente). Se pueden considerar como las curvas de sensibilidad espectral de tres detectores de luz lineales que producen los valores triestímulo de la CIE X , Y y Z. En conjunto, estas tres funciones describen al observador estándar de la CIE. ^[14] ${\overline {x}}(\lambda )$ ${\overline {y}}(\lambda )$ ${\overline {z}}(\lambda )$

Aproximación analítica

La búsqueda en tablas puede resultar poco práctica para algunas tareas computacionales. En lugar de consultar la tabla publicada, las funciones de correspondencia de colores CIE XYZ se pueden aproximar mediante una suma de funciones gaussianas , de la siguiente manera: ^[15]

Sea g ( x ) una función gaussiana por partes, definida por

g(x;\mu ,\tau _{1},\tau _{2})={\begin{cases}\exp {\bigl (}{-\tau _{1}^{2}(x-\mu )^{2}/2}{\bigr )},&x<\mu ,\\[2mu]\exp {\bigl (}{-\tau _{2}^{2}(x-\mu )^{2}/2}{\bigr )},&x\geq \mu .\end{cases}}

Es decir, g ( x ) se parece a una curva de campana con su pico en $x = μ$ , una dispersión/desviación estándar de a la izquierda de la media y una dispersión de a la derecha de la media. Con la longitud de onda λ medida en nanómetros , aproximamos las funciones de coincidencia de color de 1931: $1/\tau _{1}$ $1/\tau _{2}$

{\begin{aligned}{\overline {x}}(\lambda )&=1.056\,g(\lambda ;599.8,0.0264,0.0323)+0.362\,g(\lambda ;442.0,0.0624,0.0374)\\[2mu]&\quad -0.065\,g(\lambda ;501.1,0.0490,0.0382),\\[5mu]{\overline {y}}(\lambda )&=0.821\,g(\lambda ;568.8,0.0213,0.0247)+0.286\,g(\lambda ;530.9,0.0613,0.0322),\\[5mu]{\overline {z}}(\lambda )&=1.217\,g(\lambda ;437.0,0.0845,0.0278)+0.681\,g(\lambda ;459.0,0.0385,0.0725).\end{aligned}}

Las diferencias al cuadrado entre la aproximación anterior y las funciones de correspondencia de color xyz medidas según la CIE son menores que la varianza intraobservador encontrada en las mediciones experimentales utilizadas para formar los estándares de la CIE. También es posible utilizar menos funciones gaussianas, con una gaussiana para cada "lóbulo". La CIE 1964 se ajusta bien a una función de un solo lóbulo. ^[15]

Las funciones de correspondencia de color CIE XYZ no son negativas y conducen a coordenadas XYZ no negativas para todos los colores reales (es decir, para espectros de luz no negativos). Otros observadores, como para el espacio CIE RGB u otros espacios de color RGB , se definen mediante otros conjuntos de tres funciones de correspondencia de color, que generalmente no son no negativas, y conducen a valores triestímulo en esos otros espacios, que pueden incluir coordenadas negativas para algunos colores reales.

Cálculo de XYZ a partir de datos espectrales

Caso emisivo

Los valores triestímulo para un color con una radiancia espectral L _e,Ω,λ se dan en términos del observador estándar por:

{\begin{aligned}X&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {x}}(\lambda )\,d\lambda ,\\[6mu]Y&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {y}}(\lambda )\,d\lambda ,\\[6mu]Z&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {z}}(\lambda )\,d\lambda .\end{aligned}}

donde es la longitud de onda de la luz monocromática equivalente (medida en nanómetros ), y los límites habituales de la integral son . $\lambda$ $\lambda \in [380,780]$

Los valores de X , Y y Z están acotados si el espectro de radiancia L _e,Ω,λ está acotado.

Casos reflexivos y transmisivos

Los casos reflectivos y transmisivos son muy similares al caso emisivo, con algunas diferencias. La radiancia espectral L _e,Ω,λ se reemplaza por la reflectancia (o transmitancia ) espectral S(λ) del objeto que se mide, multiplicada por la distribución de potencia espectral del iluminante I(λ) .

{\begin{aligned}X&={\frac {K}{N}}\int _{\lambda }S(\lambda )\,I(\lambda )\,{\overline {x}}(\lambda )\,d\lambda ,\\[8mu]Y&={\frac {K}{N}}\int _{\lambda }S(\lambda )\,I(\lambda )\,{\overline {y}}(\lambda )\,d\lambda ,\\[8mu]Z&={\frac {K}{N}}\int _{\lambda }S(\lambda )\,I(\lambda )\,{\overline {z}}(\lambda )\,d\lambda ,\end{aligned}}

dónde

N=\int _{\lambda }I(\lambda )\,{\overline {y}}(\lambda )\,d\lambda ,

K es un factor de escala (generalmente 1 o 100), y es la longitud de onda de la luz monocromática equivalente (medida en nanómetros ), y los límites estándar de la integral son . $\lambda$ $\lambda \in [380,780]$

CIE-xy.mw-parser-output .vanchor>:target~.vanchor-text{background-color:#b1d2ff}@media screen{html.skin-theme-clientpref-night .mw-parser-output .vanchor>:target~.vanchor-text{background-color:#0f4dc9}}@media screen and (prefers-color-scheme:dark){html.skin-theme-clientpref-os .mw-parser-output .vanchor>:target~.vanchor-text{background-color:#0f4dc9}}diagrama de cromaticidady el espacio de color CIE xyY

Dado que el ojo humano tiene tres tipos de sensores de color que responden a diferentes rangos de longitudes de onda , una gráfica completa de todos los colores visibles es una figura tridimensional. Sin embargo, el concepto de color se puede dividir en dos partes: brillo y cromaticidad . Por ejemplo, el color blanco es un color brillante, mientras que el color gris se considera una versión menos brillante de ese mismo blanco. En otras palabras, la cromaticidad del blanco y el gris son iguales mientras que su brillo difiere.

El espacio de color CIE XYZ fue diseñado deliberadamente para que el parámetro Y sea también una medida de la luminancia de un color. La cromaticidad se especifica entonces mediante los dos parámetros derivados x e y , siendo dos de los tres valores normalizados funciones de los tres valores triestímulo X , Y y Z : ^[16]^{[ se necesita más explicación ]}

{\begin{aligned}x&={\frac {X}{X+Y+Z}}\\[5mu]y&={\frac {Y}{X+Y+Z}}\\[5mu]z&={\frac {Z}{X+Y+Z}}=1-x-y\end{aligned}}

Es decir, como cada parámetro triestímulo, X , Y , Z , se divide por la suma de los tres, los valores resultantes, x , y , z , representan cada uno una proporción del total y, por lo tanto, su suma debe ser igual a uno. Por lo tanto, el valor z se puede deducir conociendo x e y , y, en consecuencia, los dos últimos valores son suficientes para describir la cromaticidad de cualquier color.

El espacio de color derivado especificado por x , y e Y se conoce como espacio de color CIE xyY y se utiliza ampliamente para especificar colores en la práctica.

Los valores triestímulo X y Z se pueden calcular a partir de los valores de cromaticidad x e y y del valor triestímulo Y : ^[17]

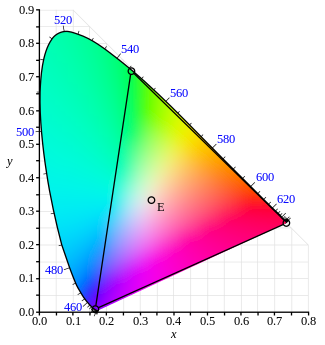
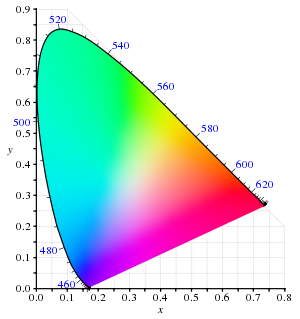
{\begin{aligned}X&={\frac {Y}{y}}x,\\[5mu]Z&={\frac {Y}{y}}(1-x-y).\end{aligned}}

La figura de la derecha muestra el diagrama de cromaticidad relacionado. El límite curvo exterior es el lugar geométrico espectral , con longitudes de onda que se muestran en nanómetros. El diagrama de cromaticidad es una herramienta para especificar cómo el ojo humano experimentará la luz con un espectro determinado. No puede especificar los colores de los objetos (o las tintas de impresión), ya que la cromaticidad observada al mirar un objeto también depende de la fuente de luz.

Matemáticamente los colores del diagrama de cromaticidad ocupan una región del plano proyectivo real .

El diagrama de cromaticidad ilustra una serie de propiedades interesantes del espacio de color CIE XYZ:

El diagrama representa todas las cromaticidades visibles para la persona promedio. Estas se muestran en color y esta región se llama la gama de la visión humana. La gama de todas las cromaticidades visibles en el gráfico CIE es la figura con forma de lengua o herradura que se muestra en color. El borde curvo de la gama se llama lugar geométrico espectral y corresponde a la luz monocromática (cada punto representa un tono puro de una sola longitud de onda), con longitudes de onda enumeradas en nanómetros. El borde recto en la parte inferior de la gama se llama línea de púrpuras . Estos colores, aunque están en el borde de la gama, no tienen contraparte en la luz monocromática. Los colores menos saturados aparecen en el interior de la figura con el blanco en el centro.
Se ve que todas las cromaticidades visibles corresponden a valores no negativos de x , y y z (y por lo tanto a valores no negativos de X , Y y Z ).
Si se eligen dos puntos de color en el diagrama de cromaticidad, todos los colores que se encuentran en línea recta entre los dos puntos se pueden formar mezclando estos dos colores. De ello se deduce que la gama de colores debe tener forma convexa . Todos los colores que se pueden formar mezclando tres fuentes se encuentran dentro del triángulo formado por los puntos de la fuente en el diagrama de cromaticidad (y así sucesivamente para múltiples fuentes).
Una mezcla igual de dos colores igualmente brillantes no se encontrará generalmente en el punto medio de ese segmento de línea . En términos más generales, una distancia en el diagrama de cromaticidad CIE xy no corresponde al grado de diferencia entre dos colores. A principios de la década de 1940, David MacAdam estudió la naturaleza de la sensibilidad visual a las diferencias de color y resumió sus resultados en el concepto de elipse de MacAdam . Basándose en el trabajo de MacAdam, se desarrollaron los espacios de color CIE 1960 , CIE 1964 y CIE 1976 , con el objetivo de lograr uniformidad perceptiva (que una distancia igual en el espacio de color corresponda a diferencias iguales en el color). Aunque fueron una mejora clara respecto del sistema CIE 1931, no estaban completamente libres de distorsión.
Se puede ver que, dadas tres fuentes reales, estas fuentes no pueden cubrir toda la gama de la visión humana. En términos geométricos, no hay tres puntos dentro de la gama que formen un triángulo que incluya toda la gama; o, dicho de manera más sencilla, la gama de la visión humana no es un triángulo.
La luz con un espectro de potencia plano en términos de longitud de onda (igual potencia en cada intervalo de 1 nm ) corresponde al punto ( x , y ) = (1/3, 1/3) .

Mezcla de colores especificados con el diagrama de cromaticidad CIE xy

Cuando se mezclan de forma aditiva dos o más colores, las coordenadas de cromaticidad x e y del color resultante (x _mix ,y _mix ) se pueden calcular a partir de las cromaticidades de los componentes de la mezcla (x ₁ ,y ₁ ; x ₂ ,y ₂ ; …; x _n ,y _n ) y sus luminancias correspondientes (L ₁ , L ₂ , …, L _n ) con las siguientes fórmulas: ^[18]

x_{\mathrm {mix} }={\frac {{\dfrac {x_{1}}{y_{1}}}L_{1}+{\dfrac {x_{2}}{y_{2}}}L_{2}+\dots +{\dfrac {x_{n}}{y_{n}}}L_{n}}{{\dfrac {L_{1}}{y_{1}}}+{\dfrac {L_{2}}{y_{2}}}+\dots +{\dfrac {L_{n}}{y_{n}}}}}\quad ,\quad y_{\mathrm {mix} }={\frac {L_{1}+L_{2}+\dots +L_{n}}{{\dfrac {L_{1}}{y_{1}}}+{\dfrac {L_{2}}{y_{2}}}+\dots +{\dfrac {L_{n}}{y_{n}}}}}

Estas fórmulas se pueden derivar de las definiciones presentadas anteriormente de las coordenadas de cromaticidad x e y aprovechando el hecho de que los valores triestímulo X, Y y Z de los componentes individuales de la mezcla son directamente aditivos. En lugar de los valores de luminancia (L ₁ , L ₂ , etc.) se puede utilizar alternativamente cualquier otra cantidad fotométrica que sea directamente proporcional al valor triestímulo Y (lo que significa naturalmente que también se puede utilizar el propio Y).

Como ya se ha mencionado, cuando se mezclan dos colores, el color resultante x _mix , y _mix se situará en el segmento de línea recta que conecta estos colores en el diagrama de cromaticidad CIE xy. Para calcular la proporción de mezcla de los colores componentes x ₁ , y ₁ y x ₂ , y ₂ que da como resultado una determinada x _mix , y _mix en este segmento de línea, se puede utilizar la fórmula

{\frac {L_{1}}{L_{2}}}={\frac {y_{1}\left(x_{2}-x_{\mathrm {mix} }\right)}{y_{2}\left(x_{\mathrm {mix} }-x_{1}\right)}}={\frac {y_{1}\left(y_{2}-y_{\mathrm {mix} }\right)}{y_{2}\left(y_{\mathrm {mix} }-y_{1}\right)}}

donde L ₁ es la luminancia del color x ₁ ,y ₁ y L ₂ la luminancia del color x ₂ ,y ₂ . Como y _mix está determinado inequívocamente por x _mix y viceversa, conocer solo uno u otro de ellos es suficiente para calcular la relación de mezcla. De acuerdo con las observaciones sobre las fórmulas para x _mix y y _mix , la relación de mezcla L ₁ /L ₂ puede expresarse perfectamente en términos de otras magnitudes fotométricas distintas de la luminancia.

Definición del espacio de color CIE XYZ

Espacio de color CIE RGB

El primer paso para desarrollar el espacio de color CIE XYZ es la medición del espacio de color CIE RGB. El espacio de color CIE RGB es uno de los muchos espacios de color RGB , que se distinguen por un conjunto particular de colores primarios monocromáticos (de una sola longitud de onda) .

^{En la década de 1920, W. David Wright [3]} y John Guild ^[4] realizaron dos experimentos independientes sobre la percepción humana del color con diez observadores. Sus resultados sentaron las bases para la especificación del espacio de color tricromático CIE XYZ.

Los experimentos se llevaron a cabo utilizando una pantalla dividida circular (un campo bipartito) de 2 grados de diámetro, que es el tamaño angular de la fóvea humana. En un lado se proyectó un color de prueba mientras que en el otro se proyectó un color ajustable por el observador. El color ajustable era una mezcla de los tres colores primarios monocromáticos, cada uno con brillo ajustable. El observador alteraba el brillo de cada uno de los tres haces primarios hasta que se observaba una coincidencia con el color de prueba.

Si el color de prueba fuera simplemente un color monocromático en la longitud de onda λ, y si pudiera ser igualado por una combinación de los tres primarios en intensidades relativas , , y respectivamente, entonces una tabulación de estos valores en varios λ estimaría tres funciones de longitud de onda. Estas son las funciones de igualación de color RGB. Cualquier distribución espectral puede ser pensada como una combinación de un número de fuentes monocromáticas en intensidades variables, de modo que (por las leyes de Grassmann ) la integración de las funciones de igualación de color con esa distribución espectral producirá las intensidades de los tres primarios necesarias para igualarla. El problema es que los tres primarios solo pueden producir colores que se encuentren dentro de su gama - el triángulo en el espacio de color formado por los primarios, que nunca toca el locus monocromático ni la línea púrpura excepto en los tres primarios. En otras palabras, no hay ninguna fuente monocromática que pueda ser igualada por una combinación de los tres primarios, excepto en las longitudes de onda de los tres primarios mismos. Sin embargo, al añadir uno de los colores primarios al color de prueba monocromático, el color de prueba se puede incorporar a la gama RGB, lo que permite realizar una coincidencia. Añadir un color primario al color de prueba monocromático es, en efecto, lo mismo que restarlo del color ajustable, lo que, por supuesto, no se puede hacer, ya que es imposible tener una intensidad negativa para ninguno de los colores primarios. ${\bar {r}}(\lambda )$ ${\bar {g}}(\lambda )$ ${\bar {b}}(\lambda )$

Para las longitudes de onda entre los primarios azul y verde, se debe agregar algo de primario rojo para permitir la coincidencia, lo que da como resultado valores negativos de . Del mismo modo, entre los primarios verde y rojo, se debe agregar algo de azul y será negativo. Para longitudes de onda por debajo de la longitud de onda del primario azul, o por encima de la longitud de onda del primario rojo, se debe agregar algo de verde y será negativo. En cada caso, las dos funciones de coincidencia de color restantes serán positivas. Se puede ver que la desviación de la gama RGB de la gama completa es bastante pequeña, excepto entre los primarios azul y verde a 435,8 y 546,1 nm. En esta banda de longitud de onda, se necesitaron agregar cantidades bastante grandes del primario rojo al color de prueba, y es en esta banda donde la función de coincidencia de color rojo tiene valores negativos bastante grandes. En sus regiones de valores negativos, las funciones de coincidencia verde y azul tienen valores negativos bastante pequeños. ${\bar {r}}(\lambda )$ ${\bar {b}}(\lambda )$ ${\bar {g}}(\lambda )$

Aunque los experimentos de Wright y Guild se llevaron a cabo utilizando varios primarios a varias intensidades, y aunque utilizaron varios observadores diferentes, todos sus resultados se resumieron mediante las funciones de coincidencia de color CIE RGB estandarizadas , , y , obtenidas utilizando tres primarios monocromáticos en longitudes de onda estandarizadas de 700 nm (rojo), 546,1 nm (verde) y 435,8 nm (azul). Las funciones de coincidencia de color (no normalizadas) son las cantidades de primarios necesarias para coincidir con el primario de prueba monocromático. Estas funciones se muestran en el gráfico de la derecha (CIE 1931). y son cero a 435,8 nm , y son cero a 546,1 nm y y son cero a 700 nm , ya que en estos casos el color de prueba es uno de los primarios. Los primarios con longitudes de onda de 546,1 nm y 435,8 nm se eligieron porque son líneas monocromáticas fácilmente reproducibles de una descarga de vapor de mercurio. Se eligió la longitud de onda de 700 nm , que en 1931 era difícil de reproducir como un haz monocromático, porque la percepción del color por parte del ojo es bastante inmutable en esta longitud de onda y, por lo tanto, pequeños errores en la longitud de onda de este primario tendrían poco efecto en los resultados. ${\overline {r}}(\lambda )$ ${\overline {g}}(\lambda )$ ${\overline {b}}(\lambda )$ ${\overline {r}}(\lambda )$ ${\overline {g}}(\lambda )$ ${\overline {r}}(\lambda )$ ${\overline {b}}(\lambda )$ ${\overline {g}}(\lambda )$ ${\overline {b}}(\lambda )$

Las funciones de igualación de color y los primarios fueron establecidos por una comisión especial de la CIE después de una considerable deliberación. ^[19] Los puntos de corte en el lado de longitud de onda corta y larga del diagrama se eligen de manera algo arbitraria; el ojo humano puede ver luz con longitudes de onda de hasta aproximadamente 810 nm , pero con una sensibilidad que es miles de veces menor que la de la luz verde. Estas funciones de igualación de color definen lo que se conoce como el "observador estándar de la CIE de 1931". En lugar de especificar el brillo de cada primario, las curvas se normalizan para tener un área constante debajo de ellas. Esta área se fija a un valor particular especificando que

\int _{0}^{\infty }{\overline {r}}(\lambda )\,d\lambda =\int _{0}^{\infty }{\overline {g}}(\lambda )\,d\lambda =\int _{0}^{\infty }{\overline {b}}(\lambda )\,d\lambda .

Las funciones de correspondencia de color normalizadas resultantes se escalan en la relación r:g:b de 1:4,5907:0,0601 para la luminancia de la fuente y 72,0962:1,3791:1 para la radiancia de la fuente , a fin de reproducir las funciones de correspondencia de color reales. Al proponer que se estandarizaran los colores primarios, la CIE estableció un sistema internacional de notación objetiva del color.

Dadas estas funciones de correspondencia de colores escaladas, los valores triestímulo RGB para un color con una distribución de potencia espectral se darían entonces mediante: $S(\lambda )$

{\begin{aligned}R&=\int _{0}^{\infty }S(\lambda )\,{\overline {r}}(\lambda )\,d\lambda ,\\[6mu]G&=\int _{0}^{\infty }S(\lambda )\,{\overline {g}}(\lambda )\,d\lambda ,\\[6mu]B&=\int _{0}^{\infty }S(\lambda )\,{\overline {b}}(\lambda )\,d\lambda .\end{aligned}}

Todos ellos son productos internos y pueden considerarse como una proyección de un espectro de dimensión infinita a un color tridimensional .

Leyes de Grassmann

Uno podría preguntarse: "¿Por qué es posible que los resultados de Wright y Guild se puedan resumir utilizando colores primarios diferentes y diferentes intensidades de las que se utilizan realmente?". También se podría preguntar: "¿Qué sucede en el caso en que los colores de prueba que se están comparando no son monocromáticos?". La respuesta a ambas preguntas se encuentra en la (casi) linealidad de la percepción humana del color. Esta linealidad se expresa en las leyes del color de Grassmann.

El espacio CIE RGB se puede utilizar para definir la cromaticidad de la forma habitual: Las coordenadas de cromaticidad son r , g y b donde:

{\begin{aligned}r&={\frac {R}{R+G+B}},\\[5mu]g&={\frac {G}{R+G+B}},\\[5mu]b&={\frac {B}{R+G+B}}.\end{aligned}}

Construcción del espacio de color CIE XYZ a partir de los datos de Wright-Guild

La gama sRGB ( izquierda ) y la gama visible bajo iluminación D65 ( derecha ) proyectadas dentro del espacio de color CIEXYZ. X y Z son los ejes horizontales; Y es el eje vertical.

La gama sRGB ( izquierda ) y la gama visible bajo iluminación D65 ( derecha ) proyectadas dentro del espacio de color CIExyY. x e y son los ejes horizontales; Y es el eje vertical.

Tras desarrollar un modelo RGB de la visión humana utilizando las funciones de correspondencia RGB de la CIE, los miembros de la comisión especial deseaban desarrollar otro espacio de color que se relacionara con el espacio de color RGB de la CIE. Se supuso que se cumplía la ley de Grassmann y que el nuevo espacio se relacionaría con el espacio RGB de la CIE mediante una transformación lineal. El nuevo espacio se definiría en términos de tres nuevas funciones de correspondencia de color , y como se describió anteriormente. Se elegiría el nuevo espacio de color de modo que tuviera las siguientes propiedades deseables: ${\overline {x}}(\lambda )$ ${\overline {y}}(\lambda )$ ${\overline {z}}(\lambda )$

Las nuevas funciones de correspondencia de colores debían ser siempre mayores o iguales a cero. En 1931, los cálculos se hacían a mano o con una regla de cálculo, y la especificación de valores positivos era una simplificación computacional útil.
La función de igualación de color sería exactamente igual a la función de eficiencia luminosa fotópica V ( λ ) para el "observador fotópico estándar CIE". ^[20] La función de luminancia describe la variación del brillo percibido con la longitud de onda. El hecho de que la función de luminancia pudiera construirse mediante una combinación lineal de las funciones de igualación de color RGB no estaba garantizado de ninguna manera, pero se podría esperar que fuera casi cierto debido a la naturaleza casi lineal de la vista humana. Nuevamente, la razón principal de este requisito fue la simplificación computacional. ${\overline {y}}(\lambda )$
Para el punto blanco de energía constante , se requirió que x = y = z = 1/3 .
En virtud de la definición de cromaticidad y del requisito de valores positivos de x e y , se puede ver que la gama de todos los colores se encontrará dentro del triángulo [1, 0], [0, 0], [0, 1]. Se requería que la gama llenara este espacio prácticamente por completo.
Se descubrió que la función de igualación de color podía establecerse en cero por encima de los 650 nm sin salirse de los límites del error experimental. Para simplificar los cálculos, se especificó que así sería. ${\overline {z}}(\lambda )$

En términos geométricos, la elección del nuevo espacio de color equivale a la elección de un nuevo triángulo en el espacio de cromaticidad rg . En la figura de arriba a la derecha, las coordenadas de cromaticidad rg se muestran en los dos ejes en negro, junto con la gama del observador estándar de 1931. Se muestran en rojo los ejes de cromaticidad CIE xy que se determinaron mediante los requisitos anteriores. El requisito de que las coordenadas XYZ no sean negativas significa que el triángulo formado por C _r , C _g , C _b debe abarcar toda la gama del observador estándar. La línea que conecta C _r y C _b está fijada por el requisito de que la función sea igual a la función de luminancia. Esta línea es la línea de luminancia cero y se denomina alicna. El requisito de que la función sea cero por encima de 650 nm significa que la línea que conecta C _g y C _r debe ser tangente a la gama en la región de K _r . Esto define la ubicación del punto C _r . El requisito de que el punto de igual energía esté definido por x = y = 1/3 impone una restricción a la línea que une C _b y C _g y, por último, el requisito de que la gama llene el espacio impone una segunda restricción a esta línea para que esté muy cerca de la gama en la región verde, lo que especifica la ubicación de C _g y C _b . La transformación descrita anteriormente es una transformación lineal del espacio RGB de la CIE al espacio XYZ. La transformación estandarizada establecida por la comisión especial de la CIE fue la siguiente: ${\overline {y}}(\lambda )$ ${\overline {z}}(\lambda )$

Los números en la matriz de conversión a continuación son exactos, con el número de dígitos especificado en las normas CIE. ^[19]

{\begin{aligned}{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}&={\begin{bmatrix}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\b_{31}&b_{32}&b_{33}\end{bmatrix}}{\begin{bmatrix}R\\G\\B\end{bmatrix}}\\[10mu]&={\begin{bmatrix}0.490\,00&0.310\,00&0.200\,00\\0.176\,97&0.812\,40&0.010\,63\\0.000\,00&0.010\,00&0.990\,00\end{bmatrix}}{\begin{bmatrix}R\\G\\B\end{bmatrix}}\end{aligned}}

La matriz anterior está equilibrada para el estímulo equienergético: tiene coordenadas (1,1,1) en coordenadas RGB y XYZ.

Si bien la matriz anterior está especificada con exactitud en las normas, la inversa no se especifica para que pueda aproximarse a la precisión de la máquina y así reducir los errores de redondeo. Sus valores se pueden calcular con precisión utilizando números racionales:

{\begin{bmatrix}R\\G\\B\end{bmatrix}}={\frac {1}{3400850}}{\begin{bmatrix}8041697&-3049000&-1591847\\-1752003&4851000&301853\\17697&-49000&3432153\end{bmatrix}}{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}

Que tiene estos valores aproximados:

{\begin{bmatrix}R\\G\\B\end{bmatrix}}\approx {\begin{bmatrix}2.364\,61385&-0.896\,54057&-0.468\,07328\\-0.515\,16621&1.426\,4081&0.088\,7581\\0.005\,2037&-0.014\,40816&1.009\,20446\end{bmatrix}}{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}

Los primarios XYZ tendrán coordenadas XYZ [1,0,0], [0,1,0] y [0,0,1] en el espacio XYZ, por lo que las columnas de la matriz inversa anterior especifican los primarios XYZ (Cr, Cg y Cb) en el espacio RGB. Dividir cada columna por su suma dará las coordenadas de los primarios XYZ en el espacio RGB, lo que da como resultado:

Cr = {1,27496, -0,27777, 0,00280576}

Cg = {-1,7393, 2,76726, -0,0279521}

Cb = {-0,743104, 0,140911, 1,60219}

Las coordenadas r y g de las primarias XYZ se indican en el diagrama del espacio de cromaticidad rg anterior.

Las integrales de las funciones de correspondencia de color XYZ deben ser todas iguales según el requisito 3 anterior, y esto se establece mediante la integral de la función de eficiencia luminosa fotópica según el requisito 2 anterior. Las curvas de sensibilidad tabuladas tienen una cierta cantidad de arbitrariedad en ellas. Las formas de las curvas de sensibilidad individuales X , Y y Z se pueden medir con una precisión razonable. Sin embargo, la curva de luminosidad general (que de hecho es una suma ponderada de estas tres curvas) es subjetiva, ya que implica preguntar a una persona de prueba si dos fuentes de luz tienen el mismo brillo, incluso si son de colores completamente diferentes. En la misma línea, las magnitudes relativas de las curvas X , Y y Z son arbitrarias. Además, se podría definir un espacio de color válido con una curva de sensibilidad X que tenga el doble de amplitud. Este nuevo espacio de color tendría una forma diferente. Las curvas de sensibilidad en los espacios de color XYZ CIE 1931 y 1964 están escaladas para tener áreas iguales bajo las curvas.

Mejoras posteriores

Se encuentran disponibles otras funciones de correspondencia de colores de estilo XYZ que corrigen problemas conocidos en el espacio de color original de 1931. Estas funciones implican sus propios espacios de color similares a XYZ y xyY. ^[21]

Correcciones de Judd y Vos para el CMF de 2°: El problema más grave con las funciones de correspondencia de color CIE XYZ de 1931 es el error en la función fotópica Y (o función en el extremo azul del espectro). ^[22] Las correcciones Judd (1951) y Vos (1978) ^[23] posteriores buscaron corregir el problema sin desviarse de la metodología original. ^[21] $V(\lambda )$
CIE 1964 X ₁₀ Y ₁₀ Z ₁₀: X ₁₀ Y ₁₀ Z ₁₀ (también escrito XYZ ₁₀ y de forma análoga para lo siguiente) es el espacio de color de estilo XYZ definido utilizando los CMF de observador de 10° CIE 1964. ^[24] Los 3 CMF se derivan principalmente de las funciones de correspondencia de color RGB de Stiles y Burch, ^[25] que a diferencia de las funciones de Wright-Guild (y las correcciones posteriores de Judd-Vos) se "miden directamente", liberándolas de los errores de reconstrucción de las funciones de 1931. ^[21]; Stiles y Burch también publicaron un conjunto de funciones de correspondencia de colores RGB 2°; sin embargo, la CIE no ha reconocido formalmente ningún espacio XYZ derivado de ellas. ^[21]
CIE _170-2_XF YF _ZF: X _F Y _F Z _F es el espacio de color de estilo XYZ definido utilizando el observador fisiológico de 2° de Stockman & Sharpe (2000), que a su vez es una combinación lineal de las funciones de respuesta del cono LMS . ^[26] Los datos CMF, junto con el conjunto de datos fisiológicos de 10°, están disponibles en el laboratorio de investigación de color y visión del University College de Londres con una resolución de hasta 0,1 nm. ^[27]
CIE 170-2 X _F,10 Y _F,10 Z _F,10: Este espacio se basa en el observador fisiológico de 10° de Stockman & Sharpe (2000). ^[26]

Según Konica Minolta , el CMF CIE 1931 más antiguo exhibe falla de metamerismo (falla en predecir cuándo los colores parecen iguales) para pantallas de amplia gama de colores que contienen emisores de banda estrecha como OLED , mientras que el CMF XYZ _F 2015 no se ve afectado. ^[28] Los manuales más antiguos de Sony recomiendan usar la corrección Judd-Vos aplicando un desplazamiento al punto blanco dependiendo de la tecnología de pantalla utilizada.

Véase también

Tricromacia
Color imposible
Espacio de color CIELAB
Iluminante estándar , la definición de punto blanco utilizada por CIE y que se muestra comúnmente en los diagramas de espacio de color como E, D50 o D65

Referencias

^ CEI (1932). Procedimientos de la Commission internationale de l'Eclairage, 1931 . Cambridge: Prensa de la Universidad de Cambridge .
^ Smith, Thomas; Guild, John (1931–32). "Los estándares colorimétricos CIE y su uso". Transactions of the Optical Society . 33 (3): 73–134. Bibcode :1931TrOS...33...73S. doi :10.1088/1475-4878/33/3/301.
^ ab Wright, William David (1928). "Una redeterminación de los coeficientes tricromáticos de los colores espectrales". Transactions of the Optical Society . 30 (4): 141–164. doi :10.1088/1475-4878/30/4/301.
^ ab Guild, J. (1932). "Las propiedades colorimétricas del espectro". Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character . 230 (681–693): 149–187. Bibcode :1932RSPTA.230..149G. doi : 10.1098/rsta.1932.0005 . JSTOR 91229. Los coeficientes tricromáticos de los diez observadores [de Wright] coincidían tan estrechamente con los de los siete observadores examinados en el National Physical Laboratory que indicaban que ambos grupos debían dar resultados que se aproximaban más a lo "normal" de lo que se podría haber esperado a partir del tamaño de cada grupo.
^ "- YouTube". YouTube . Archivado desde el original el 17 de marzo de 2016 . Consultado el 17 de octubre de 2015 .Valor triestímulo del color: representación del color independiente del dispositivo
^ Hunt, RW (1998). Medición del color (3.ª ed.). Inglaterra: Fountain Press. ISBN 0-86343-387-1.Consulte las páginas 39 a 46 para conocer las bases de la fisiología del ojo humano de los modelos de color tripartitos, y las páginas 54 a 7 para conocer las coordenadas de cromaticidad.
^ "Ragnar Granit - Estructura sensorial de la retina y la visión". www.japi.org .
^ Schanda, János, ed. (27 de julio de 2007). Colorimetría . pag. 305. doi : 10.1002/9780470175637. ISBN 9780470175637.
^ Stiles, WS; Birch, JM (1959). "Investigación de igualación de colores del NPL: Informe final (1958)". Optica Acta . 6 (1): 1–26. Código Bibliográfico :1959AcOpt...6....1S. doi :10.1080/713826267.
^ Speranskaya, NI (1959). "Determinación de las coordenadas de color del espectro para veintisiete observadores normales". Óptica y espectroscopia . 7 : 424–428.
^ "Documentos CIE gratuitos para descargar". Archivado desde el original el 28 de agosto de 2017. Consultado el 28 de agosto de 2017 .
^ Glynn, Earl F. "Informe de laboratorio de diagramas de cromaticidad".
^ "CIE 15: Informe técnico: Colorimetría, 3.ª edición". Los datos definitivos relativos a los iluminantes y observadores colorimétricos estándar son los que se dan a intervalos de 1 nm en las normas CIE correspondientes [CIE, 1998c (que se sustituirá por CIE, 2004a); CIE, 1986a].
^ Harris, AC; Weatherall, IL (septiembre de 1990). "Evaluación objetiva de la variación del color en el escarabajo de la arena Chaerodes trachyscelides White (Coleoptera: Tenebrionidae) mediante la determinación instrumental de los valores CIE LAB". Revista de la Royal Society of New Zealand . 20 (3). La Royal Society of New Zealand: 253–259. Bibcode :1990JRSNZ..20..253H. doi : 10.1080/03036758.1990.10416819 . Archivado desde el original el 8 de marzo de 2017.
^ ab Wyman, Chris; Sloan, Peter-Pike; Shirley, Peter (12 de julio de 2013). "Aproximaciones analíticas simples a las funciones de correspondencia de color CIE XYZ". Journal of Computer Graphics Techniques . 2 (2): 1-11. ISSN 2331-7418.
^ Poynton, Charles (2012). Vídeo digital y HD: algoritmos e interfaces (2.ª ed.). pág. 275. Ecuación 25.1
^ Poynton, Charles (2012). Vídeo digital y HD: algoritmos e interfaces (2.ª edición). Pág. 275. Ecuación 25.2.
^ "Comprenda la ciencia del color para maximizar el éxito con los LED: parte 2 - LEDs Magazine, número 7/2012". 18 de julio de 2012. Archivado desde el original el 11 de noviembre de 2017.
^ ab Fairman, HS; Brill, MH; Hemmendinger, H. (febrero de 1997). "Cómo se derivaron las funciones de igualación de color CIE 1931 a partir de los datos de Wright-Guild". Investigación y aplicación del color . 22 (1): 11–23. doi :10.1002/(SICI)1520-6378(199702)22:1<11::AID-COL4>3.0.CO;2-7. y Fairman, HS; Brill, MH; Hemmendinger, H. (agosto de 1998). "Fe de erratas: cómo se derivaron las funciones de correspondencia de color CIE 1931 a partir de los datos de Wright–Guild". Investigación y aplicación del color . 23 (4): 259. doi : 10.1002/(SICI)1520-6378(199808)23:4<259::AID-COL18>3.0.CO;2-7 .
^ CEI (1926). Procedimientos de la Commission internationale de l'éclairage, 1924 . Cambridge: Prensa de la Universidad de Cambridge .La función de eficiencia luminosa de 1924 subestima seriamente la sensibilidad en longitudes de onda inferiores a 460 nm y se ha complementado con curvas de luminosidad más nuevas y precisas; consulte Función de luminosidad#Mejoras al estándar .
^ abcd "Introducción al CMF". Laboratorio de investigación sobre el color y la visión . Instituto de Oftalmología, University College London. Archivado desde el original el 19 de noviembre de 2023.
^ Stockman, Andrew (diciembre de 2019). "Fundamentos de los conos y estándares CIE" (PDF) . Current Opinion in Behavioral Sciences . 30 : 87–93. doi :10.1016/j.cobeha.2019.06.005 . Consultado el 27 de octubre de 2023 .
^ Vos, JJ (septiembre de 1978). "Propiedades colorimétricas y fotométricas de un observador fundamental de 2°". Investigación y aplicación del color . 3 (3): 104–156. doi :10.1002/col.5080030309.
^ "Valor triestímulo XYZ (CIE 1931) / Valor triestímulo (CIE 1964) - Parte IV - Comunicación precisa del color". KONICA MINOLTA . Archivado desde el original el 19 de noviembre de 2023.
^ Stiles, WS; Burch, JM (1959). "Investigación de igualación de colores del NPL: informe final". Optica Acta . 6 (1). Código Bibliográfico :1959AcOpt...6....1S. doi :10.1080/713826267.
^ ab CIE 170-2:2015: Diagrama de cromaticidad fundamental con ejes fisiológicos – Parte 2: Funciones de eficiencia luminosa espectral y diagramas de cromaticidad. CIE. ISBN 978-3-902842-05-3. Archivado del original el 19 de noviembre de 2023.
^ "Funciones del CIE". Laboratorio de investigación sobre el color y la visión . Instituto de Oftalmología, University College London. Archivado desde el original el 19 de noviembre de 2023.
^ "Resolución del problema de coincidencia de colores de la pantalla" (PDF) . KONICA MINOLTA .

Lectura adicional

Broadbent, Arthur D. (agosto de 2004). "Una revisión crítica del desarrollo de las funciones de igualación de color RGB CIE1931". Color Research & Application . 29 (4): 267–272. doi :10.1002/col.20020. Este artículo describe el desarrollo de las coordenadas de cromaticidad y las funciones de igualación de color CIE1931 a partir de los datos experimentales iniciales de WD Wright y J. Guild. Se proporciona suficiente información para permitir al lector reproducir y verificar los resultados obtenidos en cada etapa de los cálculos y analizar críticamente los procedimientos utilizados. Desafortunadamente, parte de la información requerida para las transformaciones de coordenadas nunca se publicó y las tablas adjuntas proporcionan versiones probables de esos datos faltantes.
Trezona, Pat W. (2001). "Derivación de las funciones de igualación de color CIE 10° XYZ de 1964 y su aplicabilidad en fotometría". Investigación y aplicación del color . 26 (1): 67–75. doi :10.1002/1520-6378(200102)26:1<67::AID-COL7>3.0.CO;2-4.
Wright, William David (2007). "Jubileo de oro del color en la CIE: antecedentes históricos y experimentales del sistema de colorimetría de la CIE de 1931". En Schanda, János (ed.). Colorimetría . Wiley Interscience. págs. 9–24. doi :10.1002/9780470175637.ch2. ISBN 978-0-470-04904-4.(publicado originalmente por la Sociedad de Tintoreros y Coloristas , Bradford, 1981.)

Enlaces externos

Introducción a la ciencia del color, William Andrew Steer.
Informe de laboratorio y fuente Delphi sobre diagramas de cromaticidad de color de efg
Espacio de color CIE, Gernot Hoffmann
Tablas de datos descargables anotadas, Andrew Stockman y Lindsay T. Sharpe.
Cálculo a partir de los datos experimentales originales de las coordenadas de cromaticidad espectral del observador estándar RGB CIE 1931 y las funciones de correspondencia de color
Caja de herramientas MATLAB Colorlab para el cálculo de la ciencia del color y la reproducción precisa del color (por Jesús Malo y María José Luque, Universitat de Valencia). Incluye colorimetría triestímulo estándar CIE y transformaciones a una serie de modelos de apariencia de color no lineales (CIE Lab, CIE CAM, etc.).
Comunicación precisa del color Una mirada al pasado y al futuro del binning LED
[1] Medición del color en un mundo de luz