Cónica de Steiner

1. Definición de la generación de Steiner de una sección cónica

La cónica de Steiner o más precisamente la generación de una cónica de Steiner , llamada así en honor al matemático suizo Jakob Steiner , es un método alternativo para definir una sección cónica proyectiva no degenerada en un plano proyectivo sobre un cuerpo .

La definición habitual de una cónica utiliza una forma cuadrática (véase Cuadrática (geometría proyectiva) ). Otra definición alternativa de una cónica utiliza una polaridad hiperbólica . Se debe a KGC von Staudt y a veces se la denomina cónica de von Staudt . La desventaja de la definición de von Staudt es que solo funciona cuando el campo subyacente tiene una característica impar (es decir, ). ${\displaystyle Char\neq 2}$

Definición de una cónica de Steiner

• Dados dos trazos de líneas en dos puntos (todas las líneas que contienen a y respectivamente) y una aplicación proyectiva pero no perspectiva de sobre . Entonces los puntos de intersección de las líneas correspondientes forman una sección cónica proyectiva no degenerada ^{[1] [2] [3] [4]} (figura 1) ${\displaystyle B(U),B(V)}$ ${\displaystyle U,V}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle \pi }$ ${\displaystyle B(U)}$ ${\displaystyle B(V)}$

2. Mapeo de perspectiva entre líneas

Una proyección en perspectiva de un lápiz sobre otro lápiz es una biyección (correspondencia 1-1) tal que las líneas correspondientes se intersecan en una línea fija , que se denomina eje de la perspectividad (figura 2). ${\displaystyle \pi }$ ${\displaystyle B(U)}$ ${\displaystyle B(V)}$ ${\displaystyle a}$ ${\displaystyle \pi }$

Una aplicación proyectiva es un producto finito de aplicaciones de perspectiva.

Ejemplo sencillo: si se desplaza el primer punto del diagrama y su lápiz de líneas hacia y se rota el lápiz desplazado en un ángulo fijo , entonces el desplazamiento (traslación) y la rotación generan una proyección proyectiva del lápiz en el punto sobre el lápiz en . Del teorema del ángulo inscrito se obtiene: Los puntos de intersección de las líneas correspondientes forman un círculo. ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle V}$ ${\displaystyle \varphi }$ ${\displaystyle \pi }$ ${\displaystyle U}$ ${\displaystyle V}$

Ejemplos de cuerpos de uso común son los números reales , los números racionales o los números complejos . La construcción también funciona sobre cuerpos finitos, proporcionando ejemplos en planos proyectivos finitos . ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {C} }$

Observación: El teorema fundamental para planos proyectivos establece ^[5] que una aplicación proyectiva en un plano proyectivo sobre un cuerpo ( plano de Pappio ) se determina de forma única al prescribir las imágenes de tres líneas. Esto significa que, para la generación de Steiner de una sección cónica, además de dos puntos, solo se deben dar las imágenes de 3 líneas. Estos 5 elementos (2 puntos, 3 líneas) determinan de forma única la sección cónica. ${\displaystyle U,V}$

Observación: La notación "perspectiva" se debe a la doble afirmación: la proyección de los puntos de una línea desde un centro sobre una línea se llama perspectividad (ver más abajo). ^[5] ${\displaystyle a}$ ${\displaystyle Z}$ ${\displaystyle b}$

3. Ejemplo de una generación de Steiner: generación de un punto

Ejemplo

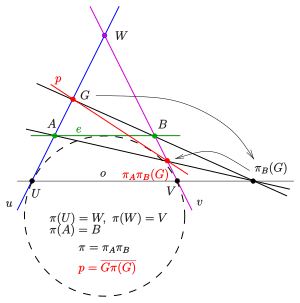
Para el siguiente ejemplo se dan las imágenes de las líneas (ver imagen): . La aplicación proyectiva es el producto de las siguientes aplicaciones de perspectiva : 1) es la aplicación en perspectiva del lápiz en el punto sobre el lápiz en el punto con eje . 2) es la aplicación en perspectiva del lápiz en el punto sobre el lápiz en el punto con eje . Primero se debe verificar que tiene las propiedades: . Por lo tanto, para cualquier línea, se puede construir la imagen y, por lo tanto, las imágenes de un conjunto arbitrario de puntos. Las líneas y contienen solo los puntos cónicos y resp.. Por lo tanto , y son líneas tangentes de la sección cónica generada. ${\displaystyle a,u,w}$ ${\displaystyle \pi (a)=b,\pi (u)=w,\pi (w)=v}$ ${\displaystyle \pi }$ ${\displaystyle \pi _{b},\pi _{a}}$ ${\displaystyle \pi _{b}}$ ${\displaystyle U}$ ${\displaystyle O}$ ${\displaystyle b}$ ${\displaystyle \pi _{a}}$ ${\displaystyle O}$ ${\displaystyle V}$ ${\displaystyle a}$ ${\displaystyle \pi =\pi _{a}\pi _{b}}$ ${\displaystyle \pi (a)=b,\pi (u)=w,\pi (w)=v}$ ${\displaystyle g}$ ${\displaystyle \pi (g)=\pi _{a}\pi _{b}(g)}$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle u}$ ${\displaystyle v}$

Una prueba de que este método genera una sección cónica se obtiene al cambiar a la restricción afín con la línea como la línea en el infinito , el punto como el origen de un sistema de coordenadas con los puntos como puntos en el infinito de los ejes x e y respectivamente y el punto . La parte afín de la curva generada parece ser la hipérbola . ^[2] ${\displaystyle w}$ ${\displaystyle O}$ ${\displaystyle U,V}$ ${\displaystyle E=(1,1)}$ ${\displaystyle y=1/x}$

Observación:

1. La generación de Steiner de una sección cónica proporciona métodos simples para la construcción de elipses , parábolas e hipérbolas , comúnmente llamados métodos del paralelogramo .
2. La figura que aparece al construir un punto (figura 3) es la degeneración de 4 puntos del teorema de Pascal . ^[6]

Generación de Steiner de una cónica dual

elipse dual

Generación de Steiner de una cónica dual

Definición de un mapeo de perspectiva

Definiciones y la generación dual

Dualizar (ver dualidad (geometría proyectiva) ) un plano proyectivo significa intercambiar los puntos con las líneas y las operaciones intersección y conexión . La estructura dual de un plano proyectivo es también un plano proyectivo. El plano dual de un plano papiano es papiano y también puede ser coordinado por coordenadas homogéneas. Una sección cónica dual no degenerada se define análogamente por una forma cuadrática.

Una cónica dual se puede generar mediante el método dual de Steiner:

• Dados los conjuntos de puntos de dos líneas y una aplicación proyectiva pero no perspectiva de sobre , entonces las líneas que conectan los puntos correspondientes forman una sección cónica proyectiva dual no degenerada. ${\displaystyle u,v}$ ${\displaystyle \pi }$ ${\displaystyle u}$ ${\displaystyle v}$

Una aplicación en perspectiva del conjunto de puntos de una línea sobre el conjunto de puntos de una línea es una biyección (correspondencia 1-1) tal que las líneas de conexión de los puntos correspondientes se intersecan en un punto fijo , que se denomina centro de la perspectividad (véase la figura). ${\displaystyle \pi }$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle Z}$ ${\displaystyle \pi }$

Una aplicación proyectiva es una secuencia finita de aplicaciones de perspectiva.

Es habitual, cuando se trata de secciones cónicas duales y comunes, llamar a la sección cónica común cónica puntual y a la cónica dual cónica lineal .

En el caso de que el campo subyacente tenga todas las tangentes de una cónica puntual intersectadas en un punto, llamado nudo (o núcleo ) de la cónica. Así, el dual de una cónica puntual no degenerada es un subconjunto de puntos de una recta dual y no una curva ovalada (en el plano dual). Así, sólo en el caso de que el dual de una cónica puntual no degenerada sea una cónica recta no degenerada. ${\displaystyle \operatorname {Char} =2}$ ${\displaystyle \operatorname {Char} \neq 2}$

Ejemplos

Doble cónica de Steiner definida por dos perspectivas ${\displaystyle \pi _{A},\pi _{B}}$

Ejemplo de una generación de Steiner de una cónica dual.

(1) Proyectividad dada por dos perspectividades: Se dan
dos rectas con punto de intersección y una proyectividad de sobre por dos perspectividades con centros . mapea recta sobre una tercera recta , mapea recta sobre recta (ver diagrama). El punto no debe estar sobre las rectas . La proyectividad es la composición de las dos perspectividades: . Por lo tanto, un punto se mapea sobre y la recta es un elemento de la cónica dual definida por . (Si fuera un punto fijo, sería perspectiva. ^[7] ) ${\displaystyle u,v}$ ${\displaystyle W}$ ${\displaystyle \pi }$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle \pi _{A},\pi _{B}}$ ${\displaystyle A,B}$ ${\displaystyle \pi _{A}}$ ${\displaystyle u}$ ${\displaystyle o}$ ${\displaystyle \pi _{B}}$ ${\displaystyle o}$ ${\displaystyle v}$ ${\displaystyle W}$ ${\displaystyle {\overline {AB}},o}$ ${\displaystyle \pi }$ ${\displaystyle \ \pi =\pi _{B}\pi _{A}}$ ${\displaystyle X}$ ${\displaystyle \pi (X)=\pi _{B}\pi _{A}(X)}$ ${\displaystyle x={\overline {X\pi (X)}}}$ ${\displaystyle \pi }$
${\displaystyle W}$ ${\displaystyle \pi }$

(2) Se dan tres puntos y sus imágenes:
El siguiente ejemplo es el dual dado anteriormente para una cónica de Steiner. Se dan
las imágenes de los puntos : . La aplicación proyectiva se puede representar mediante el producto de las siguientes perspectividades : ${\displaystyle A,U,W}$ ${\displaystyle \pi (A)=B,\,\pi (U)=W,\,\pi (W)=V}$ ${\displaystyle \pi }$ ${\displaystyle \pi _{B},\pi _{A}}$

1. ${\displaystyle \pi _{B}}$es la perspectividad del conjunto de puntos de la línea sobre el conjunto de puntos de la línea con centro . ${\displaystyle u}$ ${\displaystyle o}$ ${\displaystyle B}$
2. ${\displaystyle \pi _{A}}$es la perspectividad del conjunto de puntos de la línea sobre el conjunto de puntos de la línea con centro . ${\displaystyle o}$ ${\displaystyle v}$ ${\displaystyle A}$

Se comprueba fácilmente que la aplicación proyectiva cumple . Por lo tanto, para cualquier punto arbitrario se puede construir la imagen y la línea es un elemento de una sección cónica dual no degenerada. Como los puntos y están contenidos en las líneas , respectivamente, los puntos y son puntos de la cónica y las líneas son tangentes en . ${\displaystyle \pi =\pi _{A}\pi _{B}}$ ${\displaystyle \pi (A)=B,\,\pi (U)=W,\,\pi (W)=V}$ ${\displaystyle G}$ ${\displaystyle \pi (G)=\pi _{A}\pi _{B}(G)}$ ${\displaystyle {\overline {G\pi (G)}}}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle u,v}$ ${\displaystyle U,V}$

Cónicas intrínsecas en una geometría de incidencia lineal

La construcción de Steiner define las cónicas en una geometría de incidencia lineal plana (dos puntos determinan como máximo una línea y dos líneas se intersecan como máximo en un punto) de forma intrínseca , es decir, utilizando únicamente el grupo de colineación. En concreto, es la cónica en el punto proporcionada por la colineación , que consiste en las intersecciones de y para todas las líneas que pasan por . Si o para algún entonces la cónica es degenerada . Por ejemplo, en el plano de coordenadas real, el tipo afín (elipse, parábola, hipérbola) de está determinado por la traza y el determinante del componente matricial de , independiente de . ${\displaystyle E(T,P)}$ ${\displaystyle P}$ ${\displaystyle T}$ ${\displaystyle L}$ ${\displaystyle T(L)}$ ${\displaystyle L}$ ${\displaystyle P}$ ${\displaystyle T(P)=P}$ ${\displaystyle T(L)=L}$ ${\displaystyle L}$ ${\displaystyle E(T,P)}$ ${\displaystyle T}$ ${\displaystyle P}$

Por el contrario, el grupo de colineación del plano hiperbólico real consiste en isometrías. En consecuencia, las cónicas intrínsecas comprenden un subconjunto pequeño pero variado de las cónicas generales , curvas obtenidas de las intersecciones de cónicas proyectivas con un dominio hiperbólico. Además, a diferencia del plano euclidiano, no hay superposición entre la directa conserva la orientación y la opuesta invierte la orientación. El caso directo incluye cónicas centrales (dos líneas perpendiculares de simetría) y no centrales, mientras que cada cónica opuesta es central. Aunque las cónicas centrales directas y opuestas no pueden ser congruentes, están relacionadas por una cuasisimetría definida en términos de ángulos complementarios de paralelismo. Por lo tanto, en cualquier modelo inverso de , cada cónica central directa es biracionalmente equivalente a una cónica central opuesta. ^[8] De hecho, las cónicas centrales representan todas las curvas de género 1 con forma real invariante . Se obtiene un conjunto mínimo de representantes a partir de las cónicas directas centrales con centro y eje de simetría comunes, donde el invariante de forma es una función de la excentricidad , definida en términos de la distancia entre y . Las trayectorias ortogonales de estas curvas representan todas las curvas de género 1 con , que se manifiestan como cúbicas irreducibles o cuárticas bicirculares. Usando la ley de adición de curvas elípticas en cada trayectoria, cada cónica central general en se descompone de manera única como la suma de dos cónicas intrínsecas agregando pares de puntos donde las cónicas intersecan cada trayectoria. ^[9] ${\displaystyle \mathbb {H} ^{2}}$ ${\displaystyle E(T,P);}$ ${\displaystyle T}$ ${\displaystyle E(T,P);}$ ${\displaystyle T}$ ${\displaystyle \mathbb {H} ^{2}}$ ${\displaystyle j\geq 1}$ ${\displaystyle P}$ ${\displaystyle T(P)}$ ${\displaystyle j\leq 1}$ ${\displaystyle \mathbb {H} ^{2}}$

Notas

1. Coxeter 1993, pág. 80
2. Hartmann, pág. 38
3. Merserve 1983, pág. 65
4. Vorlesungen über synthetische Geometrie de Jacob Steiner , BG Teubner, Leipzig 1867 (de Google Books: (alemán) La parte II sigue a la parte I) Parte II, pág. 96
5. Hartmann, pág. 19
6. Hartmann, pág. 32
7. H. Lenz: Vorlesungen über projektive Geometrie , BI, Mannheim, 1965, pág.49.
8. Sarli, John (abril de 2012). "Cónicas en el plano hiperbólico intrínsecas al grupo de colineación". Journal of Geometry . 103 (1): 131–148. doi :10.1007/s00022-012-0115-5. ISSN  0047-2468. S2CID  119588289.
9. Sarli, John (22 de octubre de 2021). "La descomposición de la curva elíptica de las cónicas centrales en el plano hiperbólico real" (preimpresión). doi :10.21203/rs.3.rs-936116/v1.

Referencias

• Coxeter, HSM (1993), El plano proyectivo real , Springer Science & Business Media
• Hartmann, Erich, Geometrías circulares planas: una introducción a los planos de Moebius, Laguerre y Minkowski (PDF) , consultado el 20 de septiembre de 2014(PDF; 891 kB).
• Merserve, Bruce E. (1983) [1959], Conceptos fundamentales de geometría , Dover, ISBN 0-486-63415-9