En el aprendizaje automático , el boosting es un metaalgoritmo de conjunto que se utiliza principalmente para reducir el sesgo y la varianza. [1] Se utiliza en el aprendizaje supervisado y en una familia de algoritmos de aprendizaje automático que convierten a los estudiantes débiles en estudiantes fuertes. [2]
El concepto de boosting se basa en la pregunta planteada por Kearns y Valiant (1988, 1989): [3] [4] "¿Puede un conjunto de aprendices débiles crear un único aprendiz fuerte?" Un aprendiz débil se define como un clasificador que está solo ligeramente correlacionado con la clasificación verdadera (puede etiquetar ejemplos mejor que una suposición aleatoria). Un aprendiz fuerte es un clasificador que está arbitrariamente bien correlacionado con la clasificación verdadera. Robert Schapire respondió afirmativamente a la pregunta en un artículo publicado en 1990 [5] . Esto ha tenido ramificaciones significativas en el aprendizaje automático y las estadísticas , en particular conduciendo al desarrollo del boosting. [6]
Inicialmente, el problema de refuerzo de hipótesis simplemente se refería al proceso de convertir a un alumno débil en un alumno fuerte. [3] Los algoritmos que logran esto rápidamente se conocieron como "boosting". El arcing (Adapt[at]ive Resampling and Combining) de Freund y Schapire, [7] como técnica general, es más o menos sinónimo de refuerzo. [8]
Si bien el boosting no está limitado algorítmicamente, la mayoría de los algoritmos de boosting consisten en aprender iterativamente clasificadores débiles con respecto a una distribución y agregarlos a un clasificador fuerte final. Cuando se agregan, se ponderan de una manera que está relacionada con la precisión de los aprendices débiles. Después de agregar un aprendiz débil, los pesos de los datos se reajustan, lo que se conoce como "reponderación " . Los datos de entrada mal clasificados ganan un peso mayor y los ejemplos que se clasifican correctamente pierden peso. [nota 1] Por lo tanto, los futuros aprendices débiles se centran más en los ejemplos que los aprendices débiles anteriores clasificaron mal.
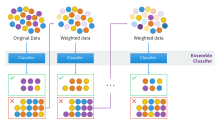
Existen muchos algoritmos de boosting. Los originales, propuestos por Robert Schapire (una formulación de puerta de mayoría recursiva ), [5] y Yoav Freund (boost por mayoría), [9] no eran adaptativos y no podían aprovechar al máximo a los estudiantes débiles. Schapire y Freund desarrollaron AdaBoost , un algoritmo de boosting adaptativo que ganó el prestigioso Premio Gödel .
Sólo los algoritmos que son algoritmos de refuerzo demostrables en la formulación de aprendizaje probablemente aproximadamente correcta pueden llamarse con precisión algoritmos de refuerzo . Otros algoritmos que son similares en espíritu [ aclaración necesaria ] a los algoritmos de refuerzo a veces se denominan "algoritmos de apalancamiento", aunque a veces también se los denomina incorrectamente algoritmos de refuerzo. [9]
La principal variación entre muchos algoritmos de boosting es su método de ponderación de los puntos de datos de entrenamiento y las hipótesis . AdaBoost es muy popular y el más significativo históricamente, ya que fue el primer algoritmo que pudo adaptarse a los estudiantes débiles. A menudo es la base de la cobertura introductoria del boosting en los cursos universitarios de aprendizaje automático. [10] Hay muchos algoritmos más recientes como LPBoost , TotalBoost, BrownBoost , xgboost , MadaBoost, LogitBoost y otros. Muchos algoritmos de boosting encajan en el marco AnyBoost, [9] que muestra que el boosting realiza un descenso de gradiente en un espacio de funciones utilizando una función de costo convexa .
Si se dan imágenes que contienen varios objetos conocidos en el mundo, se puede aprender un clasificador a partir de ellas para clasificar automáticamente los objetos en imágenes futuras. Los clasificadores simples creados en función de alguna característica de la imagen del objeto tienden a tener un rendimiento de categorización débil. El uso de métodos de refuerzo para la categorización de objetos es una forma de unificar los clasificadores débiles de una manera especial para aumentar la capacidad general de categorización. [ cita requerida ]
La categorización de objetos es una tarea típica de la visión artificial que implica determinar si una imagen contiene o no alguna categoría específica de objeto. La idea está estrechamente relacionada con el reconocimiento, la identificación y la detección. La categorización de objetos basada en la apariencia generalmente contiene la extracción de características , el aprendizaje de un clasificador y la aplicación del clasificador a nuevos ejemplos. Hay muchas formas de representar una categoría de objetos, por ejemplo, a partir del análisis de formas , modelos de bolsa de palabras o descriptores locales como SIFT , etc. Algunos ejemplos de clasificadores supervisados son los clasificadores Naive Bayes , las máquinas de vectores de soporte , las mezclas de gaussianas y las redes neuronales . Sin embargo, la investigación [¿ cuál? ] ha demostrado que las categorías de objetos y sus ubicaciones en imágenes también se pueden descubrir de manera no supervisada . [11]
El reconocimiento de categorías de objetos en imágenes es un problema desafiante en la visión por computadora , especialmente cuando el número de categorías es grande. Esto se debe a la alta variabilidad intraclase y la necesidad de generalización entre variaciones de objetos dentro de la misma categoría. Los objetos dentro de una categoría pueden verse bastante diferentes. Incluso el mismo objeto puede parecer diferente bajo diferentes puntos de vista, escala e iluminación . El desorden del fondo y la oclusión parcial también agregan dificultades al reconocimiento. [12] Los humanos pueden reconocer miles de tipos de objetos, mientras que la mayoría de los sistemas de reconocimiento de objetos existentes están entrenados para reconocer solo unos pocos, [ cuantificar ] por ejemplo, rostros humanos , automóviles , objetos simples, etc. [13] [¿ necesita actualización? ] La investigación ha sido muy activa en el manejo de más categorías y permitiendo adiciones incrementales de nuevas categorías, y aunque el problema general sigue sin resolverse, se han desarrollado varios detectores de objetos de múltiples categorías (para hasta cientos o miles de categorías [14] ). Un medio es compartir y potenciar las características .
AdaBoost se puede utilizar para la detección de rostros como un ejemplo de categorización binaria . Las dos categorías son rostros versus fondo. El algoritmo general es el siguiente:
Después de la potenciación, un clasificador construido a partir de 200 características podría producir una tasa de detección del 95 % con una tasa de falsos positivos . [15]
Otra aplicación del boosting para la categorización binaria es un sistema que detecta peatones utilizando patrones de movimiento y apariencia. [16] Este trabajo es el primero en combinar tanto la información de movimiento como la información de apariencia como características para detectar a una persona caminando. Adopta un enfoque similar al marco de detección de objetos de Viola-Jones .
En comparación con la categorización binaria, la categorización de múltiples clases busca características comunes que puedan compartirse entre las categorías al mismo tiempo. Se convierten en características más genéricas, como las de los bordes . Durante el aprendizaje, los detectores de cada categoría se pueden entrenar de forma conjunta. En comparación con el entrenamiento por separado, se generaliza mejor, se necesitan menos datos de entrenamiento y se requieren menos características para lograr el mismo rendimiento.
El flujo principal del algoritmo es similar al caso binario. Lo que es diferente es que se debe definir de antemano una medida del error de entrenamiento conjunto. Durante cada iteración, el algoritmo elige un clasificador de una sola característica (se deben fomentar las características que puedan ser compartidas por más categorías). Esto se puede hacer convirtiendo la clasificación multiclase en una binaria (un conjunto de categorías versus el resto), [17] o introduciendo un error de penalización de las categorías que no tienen la característica del clasificador. [18]
En el artículo "Sharing visual features for multiclass and multiview object detection", A. Torralba et al. utilizaron GentleBoost para el boosting y demostraron que cuando los datos de entrenamiento son limitados, el aprendizaje mediante el uso compartido de características funciona mucho mejor que no compartir, dadas las mismas rondas de boosting. Además, para un nivel de rendimiento determinado, se observa que el número total de características requeridas (y, por lo tanto, el costo de tiempo de ejecución del clasificador) para los detectores de uso compartido de características, escala aproximadamente de manera logarítmica con el número de clases, es decir, más lento que el crecimiento lineal en el caso de no compartir. Se muestran resultados similares en el artículo "Incremental learning of object detectors using a visual shape alphabet", aunque los autores utilizaron AdaBoost para el boosting.
Los algoritmos de boosting pueden basarse en algoritmos de optimización convexos o no convexos. Los algoritmos convexos, como AdaBoost y LogitBoost , pueden ser "derrotados" por el ruido aleatorio de modo que no pueden aprender combinaciones básicas y aprendibles de hipótesis débiles. [19] [20] Esta limitación fue señalada por Long y Servedio en 2008. Sin embargo, en 2009, varios autores demostraron que los algoritmos de boosting basados en optimización no convexa, como BrownBoost , pueden aprender de conjuntos de datos ruidosos y pueden aprender específicamente el clasificador subyacente del conjunto de datos Long-Servedio.
El arco [Boosting] es más exitoso que el bagging en la reducción de la varianza
El término boosting se refiere a una familia de algoritmos que pueden convertir a los estudiantes débiles en estudiantes fuertes.
Schapire (1990) demostró que el boosting es posible. (Página 823)