
Un autómata celular reversible es un autómata celular en el que cada configuración tiene un predecesor único. Es decir, es una cuadrícula regular de celdas, cada una de las cuales contiene un estado extraído de un conjunto finito de estados, con una regla para actualizar todas las celdas simultáneamente en función de los estados de sus vecinas, de modo que el estado anterior de cualquier celda antes de una actualización se puede determinar de forma única a partir de los estados actualizados de todas las celdas. La dinámica invertida en el tiempo de un autómata celular reversible siempre se puede describir mediante otra regla de autómata celular, posiblemente en un vecindario mucho más grande.
Se conocen varios métodos para definir reglas de autómatas celulares que sean reversibles; estos incluyen el método de autómata celular de bloques , en el que cada actualización divide las celdas en bloques y aplica una función invertible por separado a cada bloque, y el método de autómata celular de segundo orden , en el que la regla de actualización combina estados de dos pasos anteriores del autómata. Cuando un autómata no se define mediante uno de estos métodos, sino que se proporciona como una tabla de reglas, el problema de comprobar si es reversible es solucionable para autómatas celulares de bloques y para autómatas celulares unidimensionales, pero es indecidible para otros tipos de autómatas celulares.
Los autómatas celulares reversibles forman un modelo natural de computación reversible , una tecnología que podría conducir a dispositivos informáticos de consumo ultrabajo. Los autómatas celulares cuánticos , una forma de realizar cálculos utilizando los principios de la mecánica cuántica , a menudo deben ser reversibles. Además, muchos problemas en el modelado físico, como el movimiento de partículas en un gas ideal o el modelo de Ising de alineación de cargas magnéticas, son naturalmente reversibles y pueden simularse mediante autómatas celulares reversibles.
Las propiedades relacionadas con la reversibilidad también pueden utilizarse para estudiar autómatas celulares que no son reversibles en todo su espacio de configuración, pero que tienen un subconjunto del espacio de configuración como atractor hacia el cual convergen todas las configuraciones inicialmente aleatorias. Como escribe Stephen Wolfram , "una vez en un atractor, cualquier sistema, incluso si no tiene reglas subyacentes reversibles, debe mostrar en algún sentido una reversibilidad aproximada". [1]
Un autómata celular se define por sus celdas (a menudo una matriz unidimensional o bidimensional), un conjunto finito de valores o estados que pueden entrar en cada celda, un vecindario que asocia cada celda con un conjunto finito de celdas cercanas y una regla de actualización según la cual los valores de todas las celdas se actualizan, simultáneamente, como una función de los valores de sus celdas vecinas. Los autómatas celulares más simples posibles tienen una matriz unidimensional de celdas, cada una de las cuales puede contener un valor binario (ya sea 0 o 1), y cada celda tiene un vecindario que consiste solo en ella y sus dos celdas más cercanas a cada lado; estos se denominan autómatas celulares elementales . [2] Si la regla de actualización para un autómata de este tipo hace que cada celda permanezca siempre en el mismo estado, entonces el autómata es reversible: el estado anterior de todas las celdas se puede recuperar a partir de sus estados actuales, porque para cada celda los estados anterior y actual son los mismos. De manera similar, si la regla de actualización hace que cada celda cambie su estado de 0 a 1 y viceversa, o si hace que una celda copie el estado de una celda vecina fija, o si hace que copie un estado y luego invierta su valor, es necesariamente reversible. [3] Toffoli y Margolus (1990) llaman a estos tipos de autómatas celulares reversibles, en los que el estado de cada celda depende solo del estado anterior de una celda vecina, "triviales". A pesar de su simplicidad, la regla de actualización que hace que cada celda copie el estado de una celda vecina es importante en la teoría de la dinámica simbólica , donde se conoce como el mapa de desplazamiento . [4]
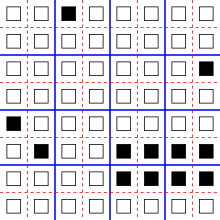
Un poco menos trivialmente, supongamos que las celdas forman nuevamente una matriz unidimensional, pero que cada estado es un par ordenado ( l , r ) que consiste en una parte izquierda l y una parte derecha r , cada una extraída de un conjunto finito de valores posibles. Defina una función de transición que establezca la parte izquierda de una celda como la parte izquierda de su vecina izquierda y la parte derecha de una celda como la parte derecha de su vecina derecha. Es decir, si el estado de la vecina izquierda es ( a , b ) y el estado de la vecina derecha es ( c , d ) , el nuevo estado de una celda es el resultado de combinar estos estados usando una operación por pares × definida por la ecuación ( a , b ) × ( c , d ) = ( a , d ) . Un ejemplo de esta construcción se da en la ilustración, en la que la parte izquierda se representa gráficamente como una forma y la parte derecha se representa como un color; en este ejemplo, cada celda se actualiza con la forma de su vecina izquierda y el color de su vecina derecha. Este autómata es reversible: los valores del lado izquierdo de cada par migran hacia la derecha y los valores del lado derecho migran hacia la izquierda, por lo que el estado anterior de cada celda se puede recuperar buscando estos valores en celdas vecinas. La operación × utilizada para combinar pares de estados en este autómata forma una estructura algebraica conocida como banda rectangular . [5]
La multiplicación de números decimales por dos o por cinco puede ser realizada por un autómata celular reversible unidimensional con diez estados por celda (los diez dígitos decimales). Cada dígito del producto depende solo de una vecindad de dos dígitos en el número dado: el dígito en la misma posición y el dígito una posición a la derecha. De manera más general, la multiplicación o división de secuencias de dígitos doblemente infinitas en cualquier base b , por un multiplicador o divisor x cuyos factores primos son también factores primos de b , es una operación que forma un autómata celular porque depende solo de un número acotado de dígitos cercanos, y es reversible debido a la existencia de inversos multiplicativos . [6] La multiplicación por otros valores (por ejemplo, la multiplicación de números decimales por tres) sigue siendo reversible, pero no define un autómata celular, porque no hay un límite fijo en el número de dígitos en el valor inicial que se necesitan para determinar un solo dígito en el resultado.
No existen autómatas celulares elementales reversibles no triviales. [7] Sin embargo, la regla 90 y otros autómatas celulares elementales basados en la función o exclusiva proporcionan un error de aproximación . En la regla 90, el estado de cada celda es el o exclusivo de los estados previos de sus dos vecinas. Este uso del o exclusivo hace que la regla de transición sea localmente invertible, en el sentido de que cualquier subsecuencia contigua de estados puede generarse mediante esta regla. La regla 90 no es una regla de autómata celular reversible, porque en la regla 90 cada asignación de estados a la matriz completa de celdas tiene exactamente cuatro predecesores posibles, mientras que se requiere que las reglas reversibles tengan exactamente un predecesor por configuración. [8]

El Juego de la Vida de Conway , una de las reglas más famosas de los autómatas celulares, no es reversible: por ejemplo, tiene muchos patrones que mueren por completo, por lo que la configuración en la que todas las células están muertas tiene muchos predecesores, y también tiene patrones del Jardín del Edén sin predecesores. Sin embargo, otra regla llamada "Critters" por sus inventores, Tommaso Toffoli y Norman Margolus , es reversible y tiene un comportamiento dinámico similar a la Vida. [9]
La regla de Critters es un autómata celular de bloques en el que, en cada paso, las celdas del autómata se dividen en bloques de 2×2 y cada bloque se actualiza independientemente de los otros bloques. Su función de transición invierte el estado de cada celda en un bloque que no tiene exactamente dos celdas vivas y, además, rota 180° los bloques con exactamente tres celdas vivas. Debido a que esta función es invertible, el autómata definido por estas reglas es un autómata celular reversible. [9]
Cuando se comienza con un campo más pequeño de células aleatorias centradas en una región más grande de células muertas, muchos patrones pequeños similares al planeador de la vida escapan del área aleatoria central e interactúan entre sí. La regla de Critters también puede soportar naves espaciales más complejas de velocidades variables, así como osciladores con una cantidad infinita de períodos diferentes. [9]
Se conocen varios métodos generales para construir reglas de autómatas celulares que sean automáticamente reversibles.
Un autómata celular de bloques es un autómata en el que, en cada paso de tiempo, las celdas del autómata se dividen en subconjuntos congruentes (llamados bloques), y la misma transformación se aplica independientemente a cada bloque. Normalmente, un autómata de este tipo utilizará más de una partición en bloques, y rotará entre estas particiones en diferentes pasos de tiempo del sistema. [10] En una forma de este diseño que se utiliza con frecuencia, llamada vecindad de Margolus, las celdas del autómata forman una cuadrícula y se dividen en bloques cuadrados más grandes de 2 × 2 en cada paso. El centro de un bloque en un paso de tiempo se convierte en la esquina de cuatro bloques en el siguiente paso de tiempo, y viceversa; de esta manera, las cuatro celdas en cada 2 × 2 pertenecen a cuatro cuadrados 2 × 2 diferentes de la partición anterior. [11] La regla de Critters analizada anteriormente es un ejemplo de este tipo de autómata.
Diseñar reglas reversibles para autómatas celulares de bloques y determinar si una regla dada es reversible es fácil: para que un autómata celular de bloques sea reversible es necesario y suficiente que la transformación aplicada a los bloques individuales en cada paso del autómata sea reversible en sí misma. Cuando un autómata celular de bloques es reversible, la versión invertida en el tiempo de su dinámica también puede describirse como un autómata celular de bloques con la misma estructura de bloques, utilizando una secuencia invertida en el tiempo de particiones de celdas en bloques, y con la función de transición para cada bloque siendo la función inversa de la regla original. [10]
Toffoli (1977) mostró cómo incorporar cualquier regla irreversible de autómata celular d -dimensional en una regla reversible ( d + 1) -dimensional. Cada porción d -dimensional de la nueva regla reversible simula un único paso de tiempo de la regla original. De esta manera, Toffoli demostró que muchas características de los autómatas celulares irreversibles, como la capacidad de simular máquinas de Turing arbitrarias , también podrían extenderse a los autómatas celulares reversibles.
Como Toffoli conjeturó y Hertling (1998) demostró, el aumento de dimensión incurrido por el método de Toffoli es un pago necesario por su generalidad: bajo supuestos suaves (tales como la invariancia de la traducción de la incrustación), cualquier incrustación de un autómata celular que tiene un Jardín del Edén en un autómata celular reversible debe aumentar la dimensión.
Morita (1995) describe otro tipo de simulación que no obedece a los supuestos de Hertling y no cambia la dimensión. El método de Morita puede simular las configuraciones finitas de cualquier autómata irreversible en el que exista un estado "quiescente" o "muerto", de modo que si una célula y todas sus vecinas están en estado quiescente, la célula permanece en estado quiescente en el siguiente paso. La simulación utiliza un autómata celular reversible en bloques de la misma dimensión que el autómata irreversible original. La información que sería destruida por los pasos irreversibles del autómata simulado se envía, en cambio, fuera de la configuración hacia la región quiescente infinita del autómata simulador. Esta simulación no actualiza todas las células del autómata simulado simultáneamente; más bien, el tiempo para simular un solo paso es proporcional al tamaño de la configuración que se está simulando. Sin embargo, la simulación conserva con precisión el comportamiento del autómata simulado, como si todas sus células se estuvieran actualizando simultáneamente. Utilizando este método es posible demostrar que incluso los autómatas celulares reversibles unidimensionales son capaces de realizar cálculos universales. [12]

La técnica del autómata celular de segundo orden es un método para transformar cualquier autómata celular en un autómata celular reversible, inventado por Edward Fredkin y publicado por primera vez por varios otros autores en 1984. [13] En esta técnica, el estado de cada célula en el autómata en el tiempo t es una función tanto de su vecindad en el tiempo t − 1 como de su propio estado en el tiempo t − 2 . Específicamente, la función de transición del autómata asigna cada vecindad en el tiempo t − 1 a una permutación en el conjunto de estados, y luego aplica esa permutación al estado en el tiempo t − 2 . La dinámica inversa del autómata se puede calcular asignando cada vecindad a la permutación inversa y procediendo de la misma manera. [14]
En el caso de autómatas con estados de valor binario (cero o uno), sólo hay dos permutaciones posibles en los estados (la permutación identidad y la permutación que intercambia los dos estados), que pueden representarse como la o exclusiva de un estado con un valor binario. De esta manera, cualquier autómata celular convencional de dos valores puede convertirse en una regla de autómata celular de segundo orden utilizando la función de transición del autómata convencional en los estados en el tiempo t − 1 , y luego calculando la o exclusiva de estos estados con los estados en el tiempo t − 2 para determinar los estados en el tiempo t . Sin embargo, el comportamiento del autómata celular reversible determinado de esta manera puede no tener ninguna semejanza con el comportamiento del autómata celular a partir del cual fue definido. [14]
Cualquier autómata de segundo orden puede transformarse en un autómata celular convencional, en el que la función de transición depende únicamente del paso de tiempo anterior, combinando pares de estados de pasos de tiempo consecutivos del autómata de segundo orden en estados individuales de un autómata celular convencional. [14]
Un autómata celular unidimensional descubierto por Patt (1971) utiliza un vecindario que consiste en cuatro celdas contiguas. En este autómata, una celda cambia su estado cada vez que ocupa la posición "?" en el patrón "0?10". No pueden superponerse dos patrones de este tipo, por lo que el mismo "paisaje" que rodea a la celda cambiada continúa estando presente después de la transición. En el siguiente paso, la celda en la misma posición "?" cambiará de nuevo, volviendo a su estado original. Por lo tanto, este autómata es su propio inverso y es reversible. Patt realizó una búsqueda de fuerza bruta de todos los autómatas celulares unidimensionales de dos estados con vecindarios pequeños; esta búsqueda condujo al descubrimiento de este autómata y demostró que era el autómata celular reversible unidimensional de dos estados no trivial más simple posible. No hay autómatas reversibles de dos estados no triviales con vecindarios de tres celdas, y todos los autómatas reversibles de dos estados con vecindarios de cuatro celdas son variantes simples del autómata de Patt. [15]
El autómata de Patt puede verse en retrospectiva como un ejemplo de la técnica del "paisaje conservado" para diseñar autómatas celulares reversibles. En esta técnica, un cambio en el estado de una célula es desencadenado por un patrón entre un conjunto de vecinos que no cambian de estado. De esta manera, la existencia del mismo patrón puede usarse para desencadenar el cambio inverso en la dinámica invertida en el tiempo del autómata. El autómata de Patt tiene una dinámica muy simple (todas las secuencias cíclicas de configuraciones tienen una longitud de dos), pero los autómatas que usan la misma técnica del paisaje conservado con más de un patrón de activación son capaces de un comportamiento más complejo. En particular, pueden simular cualquier autómata celular de segundo orden. [15]
El modelo SALT de Miller & Fredkin (2005) es un caso especial de la técnica del paisaje conservado. En este modelo, las celdas de una cuadrícula de números enteros se dividen en subconjuntos pares e impares. En cada paso de tiempo, ciertos pares de celdas de una paridad se intercambian, en función de la configuración de celdas cercanas de la otra paridad. Las reglas que utilizan este modelo pueden simular la computadora de bolas de billar [ 16] o admitir largas cadenas de celdas vivas que pueden moverse a muchas velocidades diferentes o vibrar a muchas frecuencias diferentes [17] .
Un autómata celular consiste en una matriz de celdas, cada una de las cuales tiene un número finito de estados posibles , junto con una regla para actualizar todas las celdas simultáneamente basándose únicamente en los estados de las celdas vecinas. Una configuración de un autómata celular es una asignación de un estado a cada celda del autómata; la regla de actualización de un autómata celular forma una función de configuraciones a configuraciones, con el requisito de que el valor actualizado de cualquier celda dependa únicamente de algún vecindario finito de la celda, y que la función sea invariante bajo las traslaciones de la matriz de entrada.
Con estas definiciones, un autómata celular es reversible cuando satisface cualquiera de las siguientes condiciones, todas ellas matemáticamente equivalentes entre sí: [18]
Di Gregorio y Trautteur (1975) analizan varias definiciones alternativas de reversibilidad para autómatas celulares. La mayoría de ellas resultan ser equivalentes a la inyectividad o a la sobreyectividad de la función de transición del autómata; sin embargo, hay una alternativa más que no coincide con ninguna de estas dos definiciones. Se aplica a autómatas como el Juego de la Vida que tienen un estado inactivo o muerto. En un autómata de este tipo, se puede definir una configuración como "finita" si tiene solo un número finito de células no inactivas, y se puede considerar la clase de autómatas para los cuales cada configuración finita tiene al menos un predecesor finito. Esta clase resulta ser distinta tanto de los autómatas sobreyectivos como de los inyectivos, y en algunas investigaciones posteriores, los autómatas con esta propiedad se han denominado autómatas finitos invertibles . [22]
Amoroso y Patt (1972) demostraron por primera vez que el problema de comprobar la reversibilidad de un autómata celular unidimensional dado tiene una solución algorítmica. Culik (1987) y Sutner (1991) propusieron algoritmos alternativos basados en la teoría de autómatas y en los grafos de De Bruijn , respectivamente.
Estos métodos toman un tiempo polinomial , proporcional al cuadrado del tamaño de la tabla de transición de estados del autómata de entrada. [24] Un algoritmo relacionado de Hillman (1991) determina si una regla dada es sobreyectiva cuando se aplica a matrices de celdas de longitud finita con condiciones de contorno periódicas y, de ser así, para qué longitudes.
Para un autómata celular de bloques, probar la reversibilidad también es fácil: el autómata es reversible si y solo si la función de transición en los bloques del autómata es invertible, y en este caso el autómata inverso tiene la misma estructura de bloques que la función de transición inversa. [10]
Sin embargo, para autómatas celulares con otros vecindarios en dos o más dimensiones, el problema de probar la reversibilidad es indecidible , lo que significa que no puede existir un algoritmo que siempre se detenga y siempre responda correctamente el problema. La prueba de este hecho por Kari (1990) se basa en la indecidibilidad previamente conocida de teselar el plano mediante teselas de Wang , conjuntos de teselas cuadradas con marcas en sus bordes que restringen qué pares de teselas pueden encajar borde con borde. Kari define un autómata celular a partir de un conjunto de teselas de Wang, de modo que el autómata no es inyectivo si y solo si el conjunto de teselas dado puede teselar todo el plano. Su construcción utiliza el vecindario de von Neumann y celdas con un gran número de estados. En el mismo artículo, Kari también mostró que es indecidible probar si una regla de autómata celular dada de dos o más dimensiones es sobreyectiva (es decir, si tiene un Jardín del Edén ).
En un autómata celular reversible unidimensional con n estados por célula, en el que el vecindario de una célula es un intervalo de m células, el autómata que representa la dinámica inversa tiene vecindarios que consisten en, como máximo, n m − 1 − m + 1 células. Se sabe que este límite es estricto para m = 2 : existen autómatas celulares reversibles de n estados con vecindarios de dos células cuya dinámica invertida en el tiempo forma un autómata celular con un tamaño de vecindario exactamente n − 1 . [25]
Para cualquier entero m solo hay un número finito de autómatas celulares reversibles de m estados bidimensionales con la vecindad de von Neumann. Por lo tanto, hay una función bien definida f ( m ) tal que todas las inversas de autómatas celulares de m estados con la vecindad de von Neumann usan una vecindad con radio como máximo f ( m ) : simplemente sea f ( m ) el máximo, entre todos los autómatas celulares reversibles de m estados finitos , del tamaño de vecindad necesario para representar la dinámica invertida en el tiempo del autómata. Sin embargo, debido al resultado de indecidibilidad de Kari, no hay un algoritmo para calcular f ( m ) y los valores de esta función deben crecer muy rápidamente, más rápidamente que cualquier función computable . [12]
Una clasificación bien conocida de los autómatas celulares realizada por Stephen Wolfram estudia su comportamiento en condiciones iniciales aleatorias. Para un autómata celular reversible, si la configuración inicial se elige de manera uniforme al azar entre todas las configuraciones posibles, entonces esa misma aleatoriedad uniforme continúa siendo válida para todos los estados subsiguientes. Por lo tanto, parecería que la mayoría de los autómatas celulares reversibles pertenecen a la Clase 3 de Wolfram: autómatas en los que casi todas las configuraciones iniciales evolucionan de manera pseudoaleatoria o caótica. Sin embargo, todavía es posible distinguir entre diferentes autómatas celulares reversibles analizando el efecto de las perturbaciones locales en el comportamiento del autómata. Realizar un cambio en el estado inicial de un autómata celular reversible puede hacer que los cambios en estados posteriores permanezcan solo dentro de una región limitada, se propaguen de manera irregular pero ilimitada o se extiendan rápidamente, y Wolfram (1984) enumera reglas unidimensionales para autómatas celulares reversibles que exhiben estos tres tipos de comportamiento.
Un trabajo posterior de Wolfram identifica al autómata unidimensional Rule 37R como particularmente interesante en este sentido. Cuando se ejecuta en una matriz finita de celdas con condiciones de contorno periódicas, comenzando desde una pequeña semilla de celdas aleatorias centradas dentro de un vecindario vacío más grande, tiende a fluctuar entre estados ordenados y caóticos. Sin embargo, con las mismas condiciones iniciales en un conjunto ilimitado de celdas, sus configuraciones tienden a organizarse en varios tipos de partículas móviles simples. [26]
Otra forma de formalizar los autómatas celulares reversibles implica el álgebra abstracta , y esta formalización ha sido útil para desarrollar búsquedas computarizadas de reglas de autómatas celulares reversibles. Boykett (2004) define un bigrupoide semicentral como una estructura algebraica que consiste en un conjunto S de elementos y dos operaciones → y ← sobre pares de elementos, que satisfacen los dos axiomas ecuacionales:
Por ejemplo, esto es cierto para las dos operaciones en las que operación → devuelve su argumento derecho y operación ← devuelve su argumento izquierdo. Estos axiomas generalizan el axioma definitorio (para una sola operación binaria) de un grupoide central . [5]
Como sostiene Boykett, cualquier autómata celular reversible unidimensional es equivalente a un autómata en forma rectangular , en el que las células están desplazadas media unidad en cada paso de tiempo, y en el que tanto la evolución hacia delante como la inversa del autómata tienen vecindarios con solo dos células, las células a media unidad de distancia en cada dirección. Si un autómata reversible tiene vecindarios más grandes que dos células, puede ser simulado por un autómata reversible con vecindarios más pequeños y más estados por célula, en el que cada célula del autómata simulador simula un bloque contiguo de células en el autómata simulado. Los dos axiomas de un bigroupoide semicentral son exactamente las condiciones requeridas en las funciones de transición hacia delante y hacia atrás de estos vecindarios de dos células para que sean los inversos entre sí. Es decir, cada bigroupoide semicentral define un autómata celular reversible en forma rectangular, en el que la función de transición del autómata utiliza la operación → para combinar las dos celdas de su vecindad, y en el que la operación ← define de manera similar la dinámica inversa del autómata. Todo autómata celular reversible unidimensional es equivalente a uno en esta forma. [5]
Boykett utilizó esta formulación algebraica como base para algoritmos que enumeran exhaustivamente todos los posibles autómatas celulares reversibles no equivalentes. [27]
Cuando los investigadores diseñan autómatas celulares reversibles para simular sistemas físicos, normalmente incorporan al diseño las leyes de conservación del sistema; por ejemplo, un autómata celular que simula un gas ideal debería conservar el número de partículas de gas y su momento total , ya que de lo contrario no proporcionaría una simulación precisa. Sin embargo, también ha habido alguna investigación sobre las leyes de conservación que pueden tener los autómatas celulares reversibles, independientemente de cualquier diseño intencional. El tipo típico de cantidad conservada medida en estos estudios toma la forma de una suma, sobre todos los subconjuntos contiguos de k celdas del autómata, de alguna función numérica de los estados de las celdas en cada subconjunto. Tal cantidad se conserva si, siempre que toma un valor finito, ese valor permanece automáticamente constante a través de cada paso de tiempo del autómata, y en este caso se llama un invariante de k -ésimo orden del autómata. [28]
Por ejemplo, recordemos el autómata celular unidimensional definido como un ejemplo de una banda rectangular , en la que los estados de las celdas son pares de valores ( l , r ) extraídos de los conjuntos L y R de valores izquierdos y derechos, el valor izquierdo de cada celda se mueve hacia la derecha en cada paso de tiempo, y el valor derecho de cada celda se mueve hacia la izquierda. En este caso, para cada valor izquierdo o derecho x de la banda, se puede definir una cantidad conservada, el número total de celdas que tienen ese valor. Si hay λ valores izquierdos y ρ valores derechos, entonces hay λ + ρ − 2 invariantes de primer orden independientes, y cualquier invariante de primer orden se puede representar como una combinación lineal de estos fundamentales. Las cantidades conservadas asociadas con los valores de la izquierda fluyen uniformemente hacia la derecha a una tasa constante: es decir, si el número de valores de la izquierda igual a x dentro de alguna región C de la línea toma un cierto valor en el tiempo 0 , entonces tomará el mismo valor para la región desplazada C + t /2 en el tiempo t . De manera similar, las cantidades conservadas asociadas con los valores de la derecha fluyen uniformemente hacia la izquierda. [29]
Cualquier autómata celular reversible unidimensional puede ser colocado en forma rectangular, después de lo cual su regla de transición puede ser factorizada en la acción de un bigrupoide semicentral idempotente (una regla reversible para la cual las regiones de células con un valor de estado único cambian solo en sus límites) junto con una permutación en el conjunto de estados. Los invariantes de primer orden para el levantamiento idempotente de la regla del autómata (la regla modificada formada al omitir la permutación) necesariamente se comportan como los de una banda rectangular: tienen una base de invariantes que fluyen hacia la izquierda o hacia la derecha a una tasa constante sin interacción. Los invariantes de primer orden para el autómata en general son entonces exactamente los invariantes para el levantamiento idempotente que dan igual peso a cada par de estados que pertenecen a la misma órbita de la permutación. Sin embargo, la permutación de estados en la regla puede hacer que estos invariantes se comporten de manera diferente que en el levantamiento idempotente, fluyendo de manera no uniforme y con interacciones. [29]
En los sistemas físicos, el teorema de Noether establece una equivalencia entre las leyes de conservación y las simetrías del sistema. Sin embargo, en el caso de los autómatas celulares, este teorema no se aplica directamente, porque en lugar de estar gobernado por la energía del sistema, el comportamiento del autómata está codificado en sus reglas, y se garantiza que el autómata obedecerá ciertas simetrías (invariancia de traslación tanto en el espacio como en el tiempo) independientemente de las leyes de conservación que pueda obedecer. No obstante, las cantidades conservadas de ciertos sistemas reversibles se comportan de manera similar a la energía en algunos aspectos. Por ejemplo, si diferentes regiones del autómata tienen diferentes valores promedio de alguna cantidad conservada, las reglas del autómata pueden hacer que esta cantidad se disipe, de modo que la distribución de la cantidad sea más uniforme en estados posteriores. El uso de estas cantidades conservadas como sustituto de la energía del sistema puede permitir que se lo analice utilizando métodos de la física clásica. [30]
Un autómata de gas en red es un autómata celular diseñado para simular el movimiento de partículas en un fluido o un gas ideal . En un sistema de este tipo, las partículas de gas se mueven en línea recta con velocidad constante, hasta que experimentan una colisión elástica con otras partículas. Los autómatas de gas en red simplifican estos modelos al permitir solo un número constante de velocidades (normalmente, solo una velocidad y cuatro o seis direcciones de movimiento) y al simplificar los tipos de colisión que son posibles. [31]
En concreto, el modelo de gas reticular HPP consiste en partículas que se mueven a velocidad unitaria en las cuatro direcciones paralelas al eje. Cuando dos partículas se encuentran en la misma línea en direcciones opuestas, chocan y son enviadas hacia afuera desde el punto de colisión en la línea perpendicular. Este sistema obedece las leyes de conservación de los gases físicos y produce simulaciones cuya apariencia se asemeja al comportamiento de los gases físicos. Sin embargo, se encontró que obedecía leyes de conservación adicionales poco realistas. Por ejemplo, se conserva el momento total dentro de cualquier línea individual. Además, las diferencias entre las direcciones paralelas al eje y no paralelas al eje en este modelo (su anisotropía ) son indeseablemente altas. El modelo de gas reticular FHP mejora el modelo HPP al tener partículas que se mueven en seis direcciones diferentes, en ángulos de 60 grados entre sí, en lugar de solo cuatro direcciones. En cualquier colisión frontal, las dos partículas salientes se desvían en ángulos de 60 grados de las dos partículas entrantes. Las colisiones de tres vías también son posibles en el modelo FHP y se manejan de una manera que preserva el momento total y evita las leyes de conservación agregadas no físicas del modelo HPP. [31]
Debido a que el movimiento de las partículas en estos sistemas es reversible, generalmente se implementan con autómatas celulares reversibles. En particular, tanto los autómatas de gas reticular HPP como los FHP se pueden implementar con un autómata celular de bloques de dos estados utilizando el vecindario de Margolus. [31]
El modelo de Ising se utiliza para modelar el comportamiento de los sistemas magnéticos. Consiste en una matriz de celdas, el estado de cada una de las cuales representa un espín , ya sea hacia arriba o hacia abajo . La energía del sistema se mide mediante una función que depende del número de pares de celdas vecinas que tienen el mismo espín entre sí. Por lo tanto, si una celda tiene el mismo número de vecinas en los dos estados, puede invertir su propio estado sin cambiar la energía total. Sin embargo, tal inversión conserva la energía solo si no hay dos celdas adyacentes invirtiéndose al mismo tiempo. [32]
Los modelos de autómatas celulares de este sistema dividen la red cuadrada en dos subconjuntos alternados y realizan actualizaciones en uno de los dos subconjuntos a la vez. En cada actualización, cada célula que puede voltearse lo hace. Esto define un autómata celular reversible que puede utilizarse para investigar el modelo de Ising. [32]
Fredkin y Toffoli (1982) propusieron la computadora de bolas de billar como parte de sus investigaciones sobre computación reversible . Una computadora de bolas de billar consiste en un sistema de partículas sincronizadas (las bolas de billar) que se mueven en pistas y son guiadas por un conjunto fijo de obstáculos. Cuando las partículas chocan entre sí o con los obstáculos, experimentan una colisión elástica , como lo harían las bolas de billar reales . La entrada a la computadora se codifica utilizando la presencia o ausencia de partículas en ciertas pistas de entrada, y su salida se codifica de manera similar utilizando la presencia o ausencia de partículas en las pistas de salida. Las pistas en sí pueden visualizarse como cables, y las partículas como señales booleanas transportadas en esos cables. Cuando una partícula choca con un obstáculo, se refleja en él. Esta reflexión puede interpretarse como un cambio en la dirección del cable que sigue la partícula. Dos partículas en diferentes pistas pueden colisionar, formando una puerta lógica en su punto de colisión. [33]
Como demostró Margolus (1984), las computadoras de bolas de billar pueden simularse utilizando un autómata celular de bloques reversible de dos estados con el vecindario de Margolus. En la regla de actualización de este autómata, los bloques con exactamente una célula viva giran 180°, los bloques con dos células vivas diagonalmente opuestas giran 90° y todos los demás bloques permanecen inalterados. Estas reglas hacen que las células vivas aisladas se comporten como bolas de billar, moviéndose en trayectorias diagonales. Los grupos conectados de más de una célula viva se comportan, en cambio, como los obstáculos fijos de la computadora de bolas de billar. En un apéndice, Margolus también demostró que un autómata celular de segundo orden de tres estados que utiliza el vecindario bidimensional de Moore podría simular computadoras de bolas de billar.
Una razón para estudiar modelos universales reversibles de computación, como el modelo de la bola de billar, es que teóricamente podrían conducir a sistemas informáticos reales que consuman cantidades muy bajas de energía. Según el principio de Landauer , los pasos computacionales irreversibles requieren una cierta cantidad mínima de energía por paso, pero los pasos reversibles se pueden realizar con una cantidad de energía por paso que sea arbitrariamente cercana a cero. [34] Sin embargo, para realizar cálculos utilizando menos energía que el límite de Landauer, no es suficiente que un autómata celular tenga una función de transición que sea globalmente reversible: lo que se requiere es que el cálculo local de la función de transición también se realice de manera reversible. Por ejemplo, los autómatas celulares de bloques reversibles siempre son localmente reversibles: el comportamiento de cada bloque individual implica la aplicación de una función invertible con un número finito de entradas y salidas. Toffoli y Margolus (1990) fueron los primeros en preguntar si cada autómata celular reversible tiene una regla de actualización localmente reversible. Kari (1996) demostró que para autómatas unidimensionales y bidimensionales la respuesta es positiva, y Durand-Lose (2001) demostró que cualquier autómata celular reversible podría ser simulado por un autómata celular localmente reversible (posiblemente diferente). Sin embargo, la cuestión de si cada función de transición reversible es localmente reversible sigue abierta para dimensiones superiores a dos. [35]
La regla "Tron" de Toffoli y Margolus es una regla celular de bloques reversible con el vecindario de Margolus. Cuando un bloque de 2 × 2 de celdas tiene todas el mismo estado, todas las celdas del bloque cambian de estado; en todos los demás casos, las celdas del bloque permanecen sin cambios. Como sostienen Toffoli y Margolus, la evolución de los patrones generados por esta regla se puede utilizar como un reloj para sincronizar cualquier otra regla en el vecindario de Margolus. Un autómata celular sincronizado de esta manera obedece a la misma dinámica que la regla de vecindario de Margolus estándar mientras se ejecuta en un autómata celular asincrónico . [36]
Kari (1990) propuso utilizar autómatas celulares reversibles multidimensionales como sistema de cifrado . En la propuesta de Kari, la regla del autómata celular sería la clave de cifrado. El cifrado se realizaría ejecutando la regla un paso hacia adelante, y el descifrado se realizaría ejecutándola un paso hacia atrás. Kari sugiere que un sistema como este puede utilizarse como un criptosistema de clave pública . En principio, un atacante no podría determinar algorítmicamente la clave de descifrado (la regla inversa) a partir de una clave de cifrado dada (regla de avance) debido a la indecidibilidad de la prueba de reversibilidad, por lo que la regla de avance podría hacerse pública sin comprometer la seguridad del sistema. Sin embargo, Kari no especificó qué tipos de autómatas celulares reversibles deberían utilizarse para un sistema de este tipo, ni mostró cómo un criptosistema que utilice este enfoque podría generar pares de claves de cifrado/descifrado.
Chai, Cao y Zhou (2005) han propuesto un sistema de cifrado alternativo. En su sistema, la clave de cifrado determina la regla local para cada célula de un autómata celular unidimensional. Un autómata de segundo orden basado en esa regla se ejecuta durante varias rondas en una entrada para transformarla en una salida cifrada. La propiedad de reversibilidad del autómata garantiza que cualquier mensaje cifrado se pueda descifrar ejecutando el mismo sistema en sentido inverso. En este sistema, las claves deben mantenerse en secreto, porque se utiliza la misma clave tanto para el cifrado como para el descifrado.
Los autómatas celulares cuánticos son conjuntos de autómatas cuyos estados y transiciones de estados obedecen a las leyes de la dinámica cuántica . Los autómatas celulares cuánticos fueron sugeridos como modelo de computación por Feynman (1982) y formalizados por primera vez por Watrous (1995). Varias nociones competitivas de estos autómatas aún se encuentran en investigación, muchas de las cuales requieren que los autómatas construidos de esta manera sean reversibles. [37]
Janzing (2010) se preguntó si era posible que un autómata celular fuera físicamente universal , es decir, que, para cualquier región delimitada de las células del autómata, debería ser posible rodear esa región con células cuyos estados formen un andamiaje de soporte apropiado que haga que el autómata implemente cualquier transformación arbitraria en conjuntos de estados dentro de la región. Un autómata de este tipo debe ser reversible, o al menos localmente inyectivo, porque los autómatas sin esta propiedad tienen patrones de Jardín del Edén, y no es posible implementar una transformación que cree un Jardín del Edén.
Schaeffer (2015) construyó un autómata celular reversible que es físicamente universal en este sentido. El autómata de Schaeffer es un autómata celular de bloques con dos estados y el vecindario de Margolis, estrechamente relacionado con los autómatas para el modelo de bola de billar y para el gas reticular HPP. Sin embargo, el modelo de bola de billar no es físicamente universal, ya que puede usarse para construir paredes impenetrables que impidan que el estado dentro de alguna región sea leído y transformado. En el modelo de Schaeffer, cada patrón eventualmente se descompone en partículas que se mueven diagonalmente en cuatro direcciones. Por lo tanto, su autómata no es Turing completo . Sin embargo, Schaeffer demostró que es posible rodear cualquier configuración finita con un andamiaje que se desintegra más lentamente que ella. Después de que la configuración se descompone en partículas, el andamiaje intercepta esas partículas y las usa como entrada a un sistema de circuitos booleanos construidos dentro del andamiaje. Estos circuitos pueden usarse para calcular funciones arbitrarias de la configuración inicial. El andamiaje traduce entonces la salida de los circuitos de nuevo a un sistema de partículas móviles, que convergen en la región inicial y chocan entre sí para construir una copia del estado transformado. De esta manera, el sistema de Schaeffer puede utilizarse para aplicar cualquier función a cualquier región acotada del espacio de estados, lo que demuestra que esta regla del autómata es físicamente universal. [38]