Realiza operaciones básicas como pueden ser la inserción, la búsqueda y el borrado en un tiempo del orden de O(log n).Esta estructura de datos fue inventada por Robert Tarjan y Daniel Sleator.Esta operación consiste en reorganizar el árbol para un cierto elemento, colocando éste en la raíz.Alternativamente, un algoritmo "de arriba abajo" puede combinar la búsqueda y la reorganización del árbol en una sola fase.Sin embargo, estas estructuras de datos adicionales proporcionan garantías para el peor caso, y pueden ser más eficientes en la práctica para el acceso uniforme.Uno de los peores casos para el algoritmo básico del árbol biselado es el acceso secuencial a todos los elementos del árbol de forma ordenada.Esto deja el árbol completamente des balanceado (son necesarios n accesos, cada uno de los cuales del orden de O(log n) operaciones).Volviendo a acceder al primer elemento se dispara una operación que toma del orden de O(n) operaciones para volver a balancear el árbol antes de devolver este primer elemento.Esto es un retraso significativo para esa operación final, aunque el rendimiento se amortiza si tenemos en cuenta la secuencia completa, que es del orden de O(log n).Sin embargo, investigaciones recientes muestran que si aleatoriamente volvemos a balancear el árbol podemos evitar este efecto de desbalance y dar un rendimiento similar a otros algoritmos de auto-balanceo.Incluso con claves idénticas, el rendimiento permanece amortizado del orden de O(log n).Un operación de búsqueda cuidadosamente diseñada puede devolver el nodo más a la izquierda o más a la derecha de una clave dada.Si no se encuentra, el nodo biselado será aquel que visitamos por último antes de descartar la búsqueda.Así, la raíz contendrá un sucesor o predecesor del nodo buscado.Además, si el valor de clave a insertar ya existe en el árbol, se bisela el nodo que lo contiene.Al ser un árbol binario de búsqueda y estar todos los valores de clave ordenados, podemos elegir como raíz el mayor valor del subárbol izquierdo o el menor valor de clave del derecho.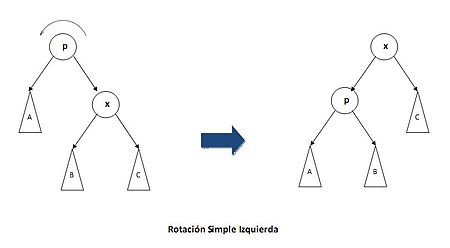Para realizar esta operación debemos rotar el árbol de forma que en cada rotación el nodo x está más cerca de la raíz.Cada biselación realizada sobre el nodo de interés mantiene el árbol parcialmente equilibrado y además los nodos recientemente accedidos se encuentran en las inmediaciones de la raíz.De esta forma amortizamos el tiempo empleado para realizar la biselación.Podríamos distinguir 3 casos generales: Si x es hijo izquierdo de p entonces realizaremos una rotación simple derecha.Entonces debemos realizar rotación doble a la derecha, en caso de que x sea hijo y nieto derecho de p y q la rotación será doble izquierda.En caso contrario, x sea hijo derecho y nieto izquierdo de q, la rotaciones simples será izquierda y después derecha.Hay muchos teoremas y conjeturas con respecto al peor caso en tiempo de ejecución para realizar una secuencia S de m accesos en un árbol biselado con n elementos.En otras palabras, los árboles biselados se comportan tan bien como los árboles de búsqueda binaria con balanceo estático en secuencias de al menos n accesos.En otras palabras, los árboles biselados se comportan tan bien como los árboles binarios de búsqueda estáticos óptimos en las secuencias de al menos n accesos.El límite superior más ajustado demostrado hasta ahora esEsta conjetura se conoce como la conjetura de optimalidad dinámica, y básicamente sostiene que los árboles biselados se comportan tan bien como cualquier otro algoritmo de búsqueda en árboles binarios hasta un factor constante.
Las rotaciones internas en árboles binarios son operaciones internas comunes muy utilizadas en árboles autobalanceables.
