Sistema de masa variable
Al añadir un término que considera el momento de la masa que se adhiere o desprende, la ecuación general de movimiento de una masa variable (que expresa el cambio del momento respecto al tiempo) puede escribirse como: Donde Fext es la fuerza neta externa ejercida en el sistema cerrado, vrel es la velocidad relativa de la masa que está escapando o ingresando con respecto al centro de masa del cuerpo, y v es la velocidad del cuerpo.
Si bien este hecho no cambia, en un sistema abierto la variación del momento ya no puede describirse como el cambio en el producto de la masa con la velocidad, pues al hacerlo se estaría olvidando al impulso asociado a la variación de masa del sistema.
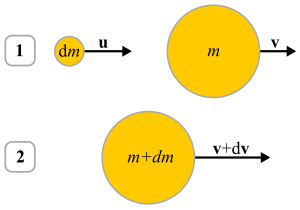
Un cuerpo con masa variable en el tiempo m se mueve con velocidad v a un tiempo inicial t. En el mismo instante, una partícula de masa dm se mueve con una velocidad u.
El momento inicial se puede escribir como:[4] Ahora, a un tiempo t + dt, el cuerpo principal y la masa puntual se acrecientan en un solo cuerpo de velocidad v + dv.
Es decir que para un cierto dt el momento del sistema sería: Entonces, por la segunda ley de Newton: Fijarse en que u - v es la velocidad de dm relativa a m, simbolizada como vrel, esta ecuación final se puede reescribir como:[5] En un sistema en el que la masa está saliendo de un cuerpo, la deducción varía ligeramente.
A un tiempo t, una masa m viaja a una velocidad v, por lo tanto el momento inicial del sistema viene dado por: Como el cuerpo principal va a estar perdiendo masa, dm será negativo, esto significa que para un tiempo t + dt el momento de sistema será: donde u es la velocidad de la masa eyectada.