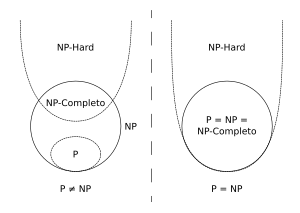
NP-hard

Esta afirmación se justifica porque si podemos encontrar un algoritmo A que resuelve uno de los problemas H de NP-hard en tiempo polinómico, entonces es posible construir un algoritmo que trabaje en tiempo polinómico para cualquier problema de NP ejecutando primero la reducción de este problema en H y luego ejecutando el algoritmo A. Asumiendo que el lenguaje L es NP-completo, En el conjunto NP-Hard se asume que el lenguaje L satisface la propiedad 2, pero no la propiedad 1.

La clase NP-completo puede definirse alternativamente como la intersección entre NP y NP-hard.

Algunas consecuencias de la definición son: Un error común es pensar que NP en NP-hard quiere decir no polinómico, ya que aunque hay serias sospechas sobre que no existen algoritmos para resolver estos problemas en tiempo polinómico, esto nunca ha sido demostrado.

Los problemas NP-hard no son todos NP, a pesar de que estas siglas aparecen es el nombre de la familia.

Sin embargo, los nombres están actualmente muy arraigados y plantear un cambio de nomenclatura resulta poco realista.