Cálculo de antenas

Los cálculos son aproximados y no tienen en cuenta, por ejemplo, el grueso de los elementos de la antena, que aquí son considerados como finos.

Tampoco se tiene en cuenta la influencia de la Tierra.

Las longitudes de los dipolos y sus separaciones son arbitrarias y no tienen tal vez ninguna utilidad en la realidad.

Los cálculos obtenidos con los programas dados como enlaces externos son probablemente más útiles en la práctica.

Salvo indicación contraria, todos los ángulos están en radianes.

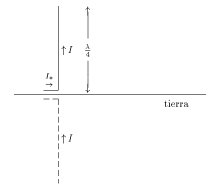
de largo colocada verticalmente sobre un plano dieléctrico o conductor que le sirve de reflector.

La imagen de la antena parece recorrida por una corriente que tiene el mismo sentido que la de la antena real.

pero que solo radia, por supuesto, hacia arriba.

Es preferible que el plano sea conductor, porque un dieléctrico solo refleja bien las ondas electromagnéticas que cuando la incidencia es rasante.

Pero en el buen lado del reflector (hacia arriba) el campo eléctrico y luego la potencia por metro cuadrado es el mismo que el producido por un dipolo

Pero como la potencia total es la mitad de la que emitiría el dipolo

ohmios, ya que la parte reactiva también está dividida por dos.

Cuando la tierra no es utilizable, como en un vehículo, se puede utilizar el techo metálico de este mismo como plano de tierra.

En otros casos se puede simular un plano de tierra con una rejilla conductora o simplemente con varillas radiales al pie del cuarto de onda.

Ese tipo de antena se llama ground-plane.

Modificando la inclinación de las varillas se modifica también el diagrama de radiación y, por supuesto, la impedancia.

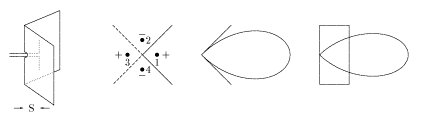
== Si, en lugar de colocar una superficie plana como reflector, se utiliza un diedro formado por superficies o rejillas metálicas las ondas emitidas por el dipolo se reflejan una o dos veces en las superficies y el resultado es equivalente a añadir antenas imágenes suplementarias.

Eso hace aparecer dos imágenes de un solo reflejo y otra de dos reflejos.

Si el ángulo hubiese sido 60° habrían aparecido 5 imágenes: 3 negativas y dos positivas.

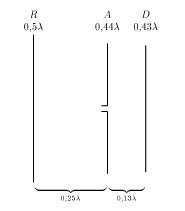
En este ejemplo, hemos puesto la separación entre el dipolo y el vértice del diedro

Como en el caso precedente solo necesitamos la primera ecuación del sistema de la describe ya que conocemos las corrientes: Sabemos que: Luego: La impedancia es En las mismas curvas que en el caso precedente encontramos: Eso nos da una impedancia de la antena: El campo eléctrico lejano es: En estas ecuaciones,

, ese campo vale: Lo que nos permite de calcular la ganancia: Puede encontrar una explicación del funcionamiento de esta antena en Yagi.

En el ejemplo de la derecha hemos construido un caso simple de antena Yagi-Uda.

Este ejemplo solo comporta un elemento alimentado de

El sistema de ecuaciones es: De la segunda ecuación deducimos: Vea que, en este caso particular, la corriente en el elemento parásito es más grande que en el elemento alimentado.

es el avance de la señal de 2 con respecto a 1 del hecho que el 2 está más cerca del punto de observación que 1: donde

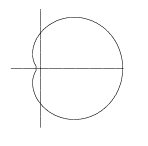
pero Como solo nos interesamos a la amplitud: En el dibujo precedente solo hemos representado el término debido a la interferencia, es decir, la raíz cuadrada en la última fórmula.

Para obtener el diagrama final aún habría que multiplicarlo por el diagrama de radiación

) el campo lejano vale: Calculemos la impedancia de la antena: El cálculo da: La ganancia de la antena es: En el dibujo de la derecha, figura una antena Yagi-Uda de tres elementos: En las curvas encontramos: El sistema de ecuaciones es: Deducimos: Después de largos y fastidiosos cálculos con números complejos, obtenemos: El campo lejano será: donde

Tomando como referencia la fase del elemento alimentado, la fase del director es: y la fase del reflector es: El campo lejano de la antena es: Y su amplitud será: Para