
La rueda Pelton o turbina Pelton es una turbina hidráulica de impulso inventada por el inventor estadounidense Lester Allan Pelton en la década de 1870. [1] [2] La rueda Pelton extrae energía del impulso del agua en movimiento, a diferencia del peso muerto del agua como la rueda hidráulica tradicional de sobrealimentación . Existieron muchas variaciones anteriores de turbinas de impulso, pero eran menos eficientes que el diseño de Pelton. El agua que salía de esas ruedas generalmente todavía tenía alta velocidad, llevándose gran parte de la energía dinámica llevada a las ruedas. La geometría de las paletas de Pelton fue diseñada de modo que cuando el borde corría a la mitad de la velocidad del chorro de agua, el agua salía de la rueda con muy poca velocidad; por lo tanto, su diseño extraía casi toda la energía de impulso del agua, lo que hacía que la turbina fuera muy eficiente.

Lester Allan Pelton nació en Vermillion, Ohio, en 1829. En 1850, viajó por tierra para participar en la Fiebre del oro de California . Pelton trabajaba vendiendo pescado que capturaba en el río Sacramento . [3] En 1860, se mudó a Camptonville , un centro de actividad minera de placer . En esa época, muchas operaciones mineras funcionaban con máquinas de vapor que consumían grandes cantidades de madera como combustible. Se utilizaban algunas ruedas hidráulicas en los ríos más grandes, pero eran ineficaces en los arroyos más pequeños que se encontraban cerca de las minas. Pelton trabajó en un diseño para una rueda hidráulica que funcionara con el caudal relativamente pequeño que se encontraba en estos arroyos. [4]
A mediados de la década de 1870, Pelton había desarrollado un prototipo de madera de su nueva rueda. En 1876, se acercó a la Miners Foundry en Nevada City, California para construir los primeros modelos comerciales en hierro. La primera rueda Pelton se instaló en la mina Mayflower en Nevada City en 1878. [4] Las ventajas de eficiencia de la invención de Pelton se reconocieron rápidamente y su producto pronto tuvo una gran demanda. Patentó su invento el 26 de octubre de 1880. [5] A mediados de la década de 1880, la Miners Foundry no pudo satisfacer la demanda y, en 1888, Pelton vendió los derechos de su nombre y las patentes de su invento a la Pelton Water Wheel Company en San Francisco. La compañía estableció una fábrica en 121/123 Main Street en San Francisco . [6]
La Pelton Water Wheel Company fabricó una gran cantidad de ruedas Pelton en San Francisco, que se enviaron a todo el mundo. En 1892, la empresa agregó una sucursal en la costa este en 143 Liberty Street en la ciudad de Nueva York . En 1900, más de 11.000 turbinas estaban en uso. En 1914, la empresa trasladó la fabricación a nuevas instalaciones más grandes en 612 Alabama Street en San Francisco. En 1956, la empresa fue adquirida por Baldwin-Lima-Hamilton Company , que puso fin a la fabricación de ruedas Pelton. [6]
En Nueva Zelanda, A & G Price, en Thames, Nueva Zelanda, produjo ruedas hidráulicas Pelton para el mercado local. Una de ellas se exhibe al aire libre en Thames Goldmine Experience.
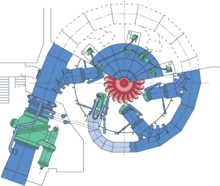
Las boquillas dirigen chorros de agua potentes y de alta velocidad contra una serie de cubos con forma de cuchara, también conocidos como palas de impulso, que están montados alrededor del borde exterior de una rueda motriz (también llamada corredor ). A medida que el chorro de agua golpea las palas, la dirección de la velocidad del agua cambia para seguir los contornos de las palas. La energía de impulso del chorro de agua ejerce un par en el sistema de cubo y rueda, haciendo girar la rueda; el chorro de agua hace un "giro en U" y sale por los lados exteriores del cubo, desacelerado a una velocidad baja. En el proceso, el impulso del chorro de agua se transfiere a la rueda y, por lo tanto, a una turbina. Por lo tanto, la energía de " impulso " realiza un trabajo en la turbina.
La máxima potencia y eficiencia se consigue cuando la velocidad del chorro de agua es el doble de la velocidad de los cangilones giratorios, lo que, suponiendo que el chorro de agua colisiona elásticamente con el cangilón, significaría que el agua sale del cangilón con velocidad cero, cediendo así toda la energía cinética a la rueda. En la práctica, un porcentaje muy pequeño de la energía cinética original del chorro de agua permanecerá en el agua, lo que hace que el cangilón se vacíe al mismo ritmo que se llena, y permite así que el flujo de entrada a alta presión continúe ininterrumpidamente y sin derroche de energía.
Normalmente se montan dos cangilones uno al lado del otro en la rueda, y el chorro de agua se divide en dos corrientes iguales; esto equilibra las fuerzas de carga lateral en la rueda y ayuda a garantizar una transferencia suave y eficiente del impulso del chorro de agua a la rueda de la turbina.
Como el agua es casi incompresible, casi toda la energía disponible se extrae en la primera etapa de la turbina hidráulica. “Por lo tanto, las ruedas Pelton tienen solo una etapa de turbina, a diferencia de las turbinas de gas que funcionan con fluido compresible”. [7]


Las ruedas Pelton son las turbinas preferidas para la energía hidroeléctrica cuando la fuente de agua disponible tiene una carga hidráulica relativamente alta a bajos caudales. Las ruedas Pelton se fabrican en todos los tamaños. Existen ruedas Pelton de varias toneladas montadas sobre cojinetes de aceite verticales en plantas hidroeléctricas . Las unidades más grandes, la central hidroeléctrica de Bieudron en el complejo de la presa Grande Dixence en Suiza, tienen más de 400 megavatios . [8]
Las ruedas Pelton más pequeñas tienen solo unos pocos centímetros de diámetro y se pueden utilizar para aprovechar la energía de los arroyos de montaña con caudales de unos pocos galones por minuto. Algunos de estos sistemas utilizan accesorios de plomería domésticos para el suministro de agua. Estas pequeñas unidades se recomiendan para su uso con 30 metros (100 pies) o más de altura de caída, a fin de generar niveles de energía significativos. Dependiendo del caudal de agua y del diseño, las ruedas Pelton funcionan mejor con alturas de caída de entre 15 y 1.800 metros (50 y 5.910 pies), aunque no existe un límite teórico.
El parámetro de velocidad específico es independiente del tamaño particular de una turbina.
En comparación con otros diseños de turbinas, la velocidad específica relativamente baja de la rueda Pelton implica que la geometría es inherentemente un diseño de " engranaje bajo ". Por lo tanto, es más adecuada para ser alimentada por una fuente hidroeléctrica con una baja relación de caudal a presión (es decir, caudal relativamente bajo y/o presión relativamente alta).
La velocidad específica es el criterio principal para asignar el tipo de turbina óptimo a un emplazamiento hidroeléctrico específico. También permite diseñar una nueva turbina a partir de un diseño existente de rendimiento conocido.
(parámetro adimensional), [9]
dónde:
La fórmula implica que la turbina Pelton está diseñada de manera más adecuada para aplicaciones con una carga hidráulica H relativamente alta , debido a que el exponente 5/4 es mayor que la unidad y dada la velocidad específica característicamente baja de la Pelton. [10]
En el caso ideal ( sin fricción ), toda la energía potencial hidráulica ( E p = mgh ) se convierte en energía cinética ( E k = mv 2 /2) (véase el principio de Bernoulli ). Igualando estas dos ecuaciones y despejando la velocidad inicial del chorro ( V i ) se indica que la velocidad teórica (máxima) del chorro es V i = √ 2 gh . Para simplificar, supongamos que todos los vectores de velocidad son paralelos entre sí. Definiendo la velocidad del rodete de la rueda como: ( u ), entonces, a medida que el chorro se acerca al rodete, la velocidad inicial del chorro relativa al rodete es: ( V i − u ). [10] La velocidad inicial del chorro es V i
Suponiendo que la velocidad del chorro es mayor que la velocidad del rodete, para que el agua no se estanque en el rodete, debido a la conservación de la masa, la masa que entra en el rodete debe ser igual a la masa que sale del rodete. Se supone que el fluido es incompresible (una suposición precisa para la mayoría de los líquidos). Además, se supone que el área de la sección transversal del chorro es constante. La velocidad del chorro permanece constante en relación con el rodete. Por lo tanto, a medida que el chorro se aleja del rodete, la velocidad del chorro en relación con el rodete es: − ( V i − u ) = − V i + u . En el marco de referencia estándar (en relación con la Tierra), la velocidad final es entonces: V f = (− V i + u) + u = − V i + 2 u .
La velocidad ideal del rodete hará que toda la energía cinética del chorro se transfiera a la rueda. En este caso, la velocidad final del chorro debe ser cero. Si − V i + 2 u = 0, entonces la velocidad óptima del rodete será u = V i /2, o la mitad de la velocidad inicial del chorro.
Por la segunda y tercera leyes de Newton , la fuerza F impuesta por el chorro sobre el corredor es igual pero opuesta a la tasa de cambio de momento del fluido, por lo que
donde ρ es la densidad y Q es el caudal volumétrico del fluido. Si D es el diámetro de la rueda, el par sobre el rodete es.
El par es máximo cuando el rodete está parado (es decir, cuando u = 0, T = ρQDV i ). Cuando la velocidad del rodete es igual a la velocidad inicial del chorro, el par es cero (es decir, cuando u = V i , entonces T = 0). En un gráfico del par en función de la velocidad del rodete, la curva del par es recta entre estos dos puntos: (0, pQDV i ) y ( V i , 0). [10] La eficiencia de la boquilla es la relación entre la potencia del chorro y la potencia del agua en la base de la boquilla.
La potencia P = Fu = Tω , donde ω es la velocidad angular de la rueda. Sustituyendo por F , tenemos P = 2 ρQ ( V i − u ) u . Para encontrar la velocidad del corredor a máxima potencia, tome la derivada de P con respecto a u e iguálela a cero, [ dP / du = 2 ρQ ( V i − 2 u )]. La potencia máxima ocurre cuando u = V i /2. P max = ρQV i 2 /2. Sustituyendo la potencia inicial del chorro V i = √ 2 gh , esto se simplifica a P max = ρghQ . Esta cantidad es exactamente igual a la potencia cinética del chorro, por lo que en este caso ideal, la eficiencia es del 100%, ya que toda la energía del chorro se convierte en salida del eje. [10]
La potencia de la rueda dividida por la potencia inicial del chorro es la eficiencia de la turbina, η = 4 u ( V i − u )/ V i 2 . Es cero para u = 0 y para u = V i . Como indican las ecuaciones, cuando una rueda Pelton real está funcionando cerca de la máxima eficiencia, el fluido fluye fuera de la rueda con muy poca velocidad residual. [10] En teoría, la eficiencia energética varía solo con la eficiencia de la boquilla y la rueda, y no varía con la carga hidráulica. [11] El término "eficiencia" puede referirse a: hidráulica, mecánica, volumétrica, de la rueda o general.
El conducto que lleva agua a alta presión a la rueda de impulsión se llama tubería forzada . Originalmente, tubería forzada era el nombre de la válvula, pero el término se ha extendido para incluir todos los sistemas hidráulicos de suministro de fluido. Tubería forzada se utiliza ahora como un término general para un paso y control de agua que está bajo presión, ya sea que alimente una turbina de impulsión o no. [10]