Transformación activa y pasiva

Distinción entre significados de las transformaciones espaciales euclidianas

En la transformación activa (izquierda), un punto P se transforma en el punto P ′ girando en el sentido de las agujas del reloj un ángulo θ alrededor del origen de un sistema de coordenadas fijo. En la transformación pasiva (derecha), el punto P permanece fijo, mientras que el sistema de coordenadas gira en sentido antihorario un ángulo θ alrededor de su origen. Las coordenadas de P ′ después de la transformación activa con respecto al sistema de coordenadas original son las mismas que las coordenadas de P con respecto al sistema de coordenadas rotado.

Las transformaciones geométricas se pueden distinguir en dos tipos: transformaciones activas o de coartada que cambian la posición física de un conjunto de puntos en relación con un marco de referencia fijo o sistema de coordenadas ( alibi significa "estar en otro lugar al mismo tiempo"); y transformaciones pasivas o de alias que dejan puntos fijos pero cambian el marco de referencia o el sistema de coordenadas con respecto al cual se describen ( alias que significa "con un nombre diferente"). ^{[1] [2]} Por transformación , los matemáticos generalmente se refieren a transformaciones activas, mientras que los físicos y los ingenieros podrían referirse a cualquiera de las dos. ^{[ cita necesaria ]}

Por ejemplo, las transformaciones activas son útiles para describir posiciones sucesivas de un cuerpo rígido . Por otro lado, las transformaciones pasivas pueden ser útiles en el análisis del movimiento humano para observar el movimiento de la tibia en relación con el fémur , es decir, su movimiento en relación con un sistema de coordenadas ( local ) que se mueve junto con el fémur, en lugar de un ( global ) sistema de coordenadas que está fijado al suelo. ^[2]

En el espacio euclidiano tridimensional , cualquier transformación rígida propia , ya sea activa o pasiva, puede representarse como un desplazamiento de tornillo , la composición de una traslación a lo largo de un eje y una rotación alrededor de ese eje.

Los términos transformación activa y transformación pasiva fueron introducidos por primera vez en 1957 por Valentine Bargmann para describir las transformaciones de Lorentz en la relatividad especial . ^[3]

Ejemplo

Rotación considerada como una transformación pasiva ( alias ) o activa ( alibi )

Traslación y rotación como transformaciones pasivas ( alias ) o activas ( alibi )

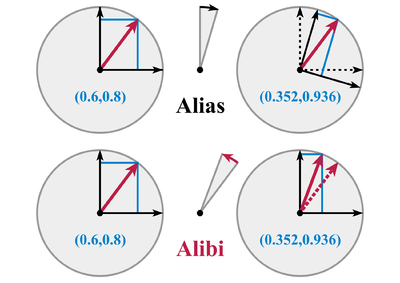
Como ejemplo, sea el vector , un vector en el plano. Una rotación del vector a través de un ángulo θ en sentido antihorario viene dada por la matriz de rotación : ${\displaystyle \mathbf {v} =(v_{1},v_{2})\in \mathbb {R} ^{2}}$

$${\displaystyle R={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{pmatrix}},}$$

transformación activatransformación pasivala matriz

Transformaciones espaciales en el espacio euclidiano R 3

En general, una transformación espacial puede consistir en una traslación y una transformación lineal. A continuación, se omitirá la traducción y la transformación lineal se representará mediante una matriz de 3 × 3 . ${\displaystyle T\colon \mathbb {R} ^{3}\to \mathbb {R} ^{3}}$ ${\displaystyle T}$

Transformación activa

Como transformación activa, transforma el vector inicial en un nuevo vector . ${\displaystyle T}$ ${\displaystyle \mathbf {v} =(v_{x},v_{y},v_{z})}$ ${\displaystyle \mathbf {v} '=(v'_{x},v'_{y},v'_{z})=T\mathbf {v} =T(v_{x},v_{y},v_{z})}$

Si se ve como una nueva base , entonces las coordenadas del nuevo vector en la nueva base son las mismas que las de la base original. Tenga en cuenta que las transformaciones activas tienen sentido incluso como una transformación lineal a un espacio vectorial diferente . Tiene sentido escribir el nuevo vector en la base no primada (como arriba) solo cuando la transformación es del espacio a sí mismo. ${\displaystyle \{\mathbf {e} '_{x}=T(1,0,0),\ \mathbf {e} '_{y}=T(0,1,0),\ \mathbf {e} '_{z}=T(0,0,1)\}}$ ${\displaystyle \mathbf {v} '=v_{x}\mathbf {e} '_{x}+v_{y}\mathbf {e} '_{y}+v_{z}\mathbf {e} '_{z}}$ ${\displaystyle \mathbf {v} =v_{x}\mathbf {e} _{x}+v_{y}\mathbf {e} _{y}+v_{z}\mathbf {e} _{z}}$

Transformación pasiva

Por otro lado, cuando se ve como una transformación pasiva, el vector inicial se deja sin cambios, mientras que el sistema de coordenadas y sus vectores base se transforman en la dirección opuesta, es decir, con la transformación inversa . ^[4] Esto da un nuevo sistema de coordenadas XYZ con vectores base: ${\displaystyle T}$ ${\displaystyle \mathbf {v} =(v_{x},v_{y},v_{z})}$ ${\displaystyle T^{-1}}$

$${\displaystyle \mathbf {e} _{X}=T^{-1}(1,0,0),\ \mathbf {e} _{Y}=T^{-1}(0,1,0),\ \mathbf {e} _{Z}=T^{-1}(0,0,1)}$$

Las nuevas coordenadas con respecto al nuevo sistema de coordenadas XYZ vienen dadas por: ${\displaystyle (v_{X},v_{Y},v_{Z})}$ ${\displaystyle \mathbf {v} }$

$${\displaystyle \mathbf {v} =(v_{x},v_{y},v_{z})=v_{X}\mathbf {e} _{X}+v_{Y}\mathbf {e} _{Y}+v_{Z}\mathbf {e} _{Z}=T^{-1}(v_{X},v_{Y},v_{Z}).}$$

De esta ecuación se ve que las nuevas coordenadas están dadas por

$${\displaystyle (v_{X},v_{Y},v_{Z})=T(v_{x},v_{y},v_{z}).}$$

Como transformación pasiva, se transforman las antiguas coordenadas en nuevas. ${\displaystyle T}$

Tenga en cuenta la equivalencia entre los dos tipos de transformaciones: las coordenadas del nuevo punto en la transformación activa y las nuevas coordenadas del punto en la transformación pasiva son las mismas, es decir

$${\displaystyle (v_{X},v_{Y},v_{Z})=(v'_{x},v'_{y},v'_{z}).}$$

En espacios vectoriales abstractos

La distinción entre transformaciones activas y pasivas se puede ver matemáticamente considerando espacios vectoriales abstractos .

Fije un espacio vectorial de dimensión finita sobre un campo (considerado como o ) y una base de . Esta base proporciona un isomorfismo a través del mapa de componentes . ${\displaystyle V}$ ${\displaystyle K}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle {\mathcal {B}}=\{e_{i}\}_{1\leq i\leq n}}$ ${\displaystyle V}$ ${\displaystyle C:K^{n}\rightarrow V}$ ${\textstyle (v_{i})_{1\leq i\leq n}=(v_{1},\cdots ,v_{n})\mapsto \sum _{i}v_{i}e_{i}}$

Una transformación activa es entonces un endomorfismo en , es decir, una aplicación lineal de hacia sí mismo. Tomando tal transformación , un vector se transforma como . Los componentes de con respecto a la base se definen mediante la ecuación . Luego, los componentes de transformar como . ${\displaystyle V}$ ${\displaystyle V}$ ${\displaystyle \tau \in {\text{End}}(V)}$ ${\displaystyle v\in V}$ ${\displaystyle v\mapsto \tau v}$ ${\displaystyle \tau }$ ${\displaystyle {\mathcal {B}}}$ ${\textstyle \tau e_{i}=\sum _{j}\tau _{ji}e_{j}}$ ${\displaystyle v}$ ${\displaystyle v_{i}\mapsto \tau _{ij}v_{j}}$

Una transformación pasiva es, en cambio, un endomorfismo en . Esto se aplica a los componentes: . Siempre que sea invertible, la nueva base se determina preguntando eso , de donde se puede derivar la expresión. ${\displaystyle K^{n}}$ ${\displaystyle v_{i}\mapsto T_{ij}v_{j}=:v'_{i}}$ ${\displaystyle T}$ ${\displaystyle {\mathcal {B}}'=\{e'_{i}\}}$ ${\displaystyle v_{i}e_{i}=v'_{i}e'_{i}}$ ${\displaystyle e'_{i}=(T^{-1})_{ji}e_{j}}$

Aunque los espacios y son isomorfos, no lo son canónicamente isomorfos. Sin embargo, la elección de la base permite la construcción de un isomorfismo. ${\displaystyle {\text{End}}(V)}$ ${\displaystyle {\text{End}}({K^{n}})}$ ${\displaystyle {\mathcal {B}}}$

Como acciones de izquierda y derecha

A menudo uno se limita al caso en el que los mapas son invertibles, de modo que las transformaciones activas son el grupo lineal general de transformaciones mientras que las transformaciones pasivas son el grupo . ${\displaystyle {\text{GL}}(V)}$ ${\displaystyle {\text{GL}}(n,K)}$

Entonces se puede entender que las transformaciones actúan sobre el espacio de bases para . Una transformación activa envía la base . Mientras tanto, una transformación pasiva envía la base . ${\displaystyle V}$ ${\displaystyle \tau \in {\text{GL}}(V)}$ ${\displaystyle \{e_{i}\}\mapsto \{\tau e_{i}\}}$ ${\displaystyle T\in {\text{GL}}(n,K)}$ ${\textstyle \{e_{i}\}\mapsto \left\{\sum _{j}(T^{-1})_{ji}e_{j}\right\}}$

Lo inverso en la transformación pasiva garantiza que los componentes se transformen de manera idéntica bajo y . Esto da entonces una clara distinción entre transformaciones activas y pasivas: las transformaciones activas actúan desde la izquierda sobre las bases, mientras que las transformaciones pasivas actúan desde la derecha, debido a lo inverso. ${\displaystyle \tau }$ ${\displaystyle T}$

Esta observación se vuelve más natural al considerar las bases como una elección de isomorfismo . El espacio de bases es equivalente al espacio de tales isomorfismos, denotado . Las transformaciones activas, identificadas con , actúan desde la izquierda por composición, mientras que las transformaciones pasivas, identificadas con, actúan desde la derecha por precomposición. ${\displaystyle {\mathcal {B}}}$ ${\displaystyle \Phi _{\mathcal {B}}:V\rightarrow K^{n}}$ ${\displaystyle {\text{Iso}}(V,K^{n})}$ ${\displaystyle {\text{GL}}(V)}$ ${\displaystyle {\text{Iso}}(V,K^{n})}$ ${\displaystyle {\text{GL}}(n,K)}$ ${\displaystyle {\text{Iso}}(V,K^{n})}$

Esto convierte el espacio de las bases en un torsor izquierdo y un torsor derecho . ${\displaystyle {\text{GL}}(V)}$ ${\displaystyle {\text{GL}}(n,K)}$

Desde una perspectiva física, las transformaciones activas se pueden caracterizar como transformaciones del espacio físico, mientras que las transformaciones pasivas se caracterizan como redundancias en la descripción del espacio físico. Esto juega un papel importante en la teoría matemática de calibre , donde las transformaciones de calibre se describen matemáticamente mediante mapas de transición que actúan desde la derecha sobre las fibras.

Ver también

• Cambio de base
• Covarianza y contravarianza de vectores.
• Rotación de ejes
• Traducción de ejes

Referencias

1. Calambres, M.; Pirani, FAE (1986). Geometría diferencial aplicable. Prensa de la Universidad de Cambridge. pag. 22.
2. Joseph K. Davidson, Kenneth Henderson Hunt (2004). "§4.4.1 La interpretación activa y la transformación activa". Robots y teoría de tornillos: aplicaciones de la cinemática y la estática a la robótica . Prensa de la Universidad de Oxford. pag. 74 y sigs . ISBN 0-19-856245-4.
3. Bargmann, Valentín (1957). "Relatividad". Reseñas de Física Moderna . 29 (2): 161-174. doi :10.1103/RevModPhys.29.161.
4. Amidror, Isaac (2007). "Apéndice D: Observación D.12". La teoría del fenómeno Moiré: Capas aperiódicas . Saltador. pag. 346.ISBN _ 978-1-4020-5457-0.

• Dirk Struik (1953) Conferencias sobre geometría analítica y proyectiva , página 84, Addison-Wesley .

enlaces externos

• Ambigüedad de la interfaz de usuario