Un telescopio anastigmat de tres espejos es un telescopio anastigmatizado construido con tres espejos curvos, lo que le permite minimizar las tres aberraciones ópticas principales: aberración esférica , coma y astigmatismo . Esto se utiliza principalmente para permitir campos de visión amplios, mucho más grandes que los posibles con telescopios con solo una o dos superficies curvas.
Un telescopio con un solo espejo curvo, como un telescopio newtoniano , siempre tendrá aberraciones. Si el espejo es esférico, sufrirá aberración esférica. Si el espejo se hace parabólico, para corregir la aberración esférica, entonces necesariamente debe sufrir coma y astigmatismo fuera del eje. Con dos espejos curvos, como el telescopio Ritchey-Chrétien , también se puede minimizar la coma. Esto permite un campo de visión útil más grande y el astigmatismo restante es simétrico alrededor de los objetos distorsionados, lo que permite la astrometría en todo el amplio campo de visión. Sin embargo, el astigmatismo se puede reducir incluyendo un tercer elemento óptico curvo. Cuando este elemento es un espejo, el resultado es un anastigmat de tres espejos . En la práctica, el diseño también puede incluir cualquier número de espejos plegables planos , utilizados para doblar la trayectoria óptica en configuraciones más convenientes.
Se pueden utilizar muchas combinaciones de tres figuras especulares para cancelar todas las aberraciones de tercer orden. En general, esto implica resolver un conjunto de ecuaciones relativamente complicado. Sin embargo, algunas configuraciones son lo suficientemente simples como para diseñarlas a partir de algunos conceptos intuitivos.
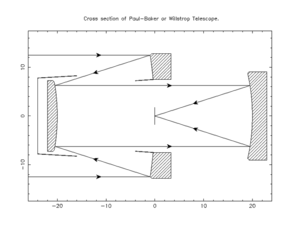
Los primeros fueron propuestos en 1935 por Maurice Paul. [1] La idea básica detrás de la solución de Paul es que los espejos esféricos, con un tope de apertura en el centro de la curvatura, solo tienen aberración esférica, sin coma ni astigmatismo (pero sí producen una imagen en una superficie curva de la mitad del radio de curvatura del espejo esférico). Por lo tanto, si se puede corregir la aberración esférica, se puede obtener un campo de visión muy amplio. Esto es similar al diseño convencional de Schmidt , pero el Schmidt lo hace con una placa correctora refractiva en lugar de un tercer espejo.
La idea de Paul era empezar con un compresor de haz Mersenne, que parece un Cassegrain hecho de dos paraboloides (confocales) , con los haces de entrada y de salida colimados. El haz de entrada comprimido se dirige entonces a un espejo terciario esférico, lo que da lugar a la aberración esférica tradicional. La idea clave de Paul es que el secundario puede convertirse entonces de nuevo en un espejo esférico.
Una forma de ver esto es imaginar que el espejo terciario, que sufre de aberración esférica, es reemplazado por un telescopio Schmidt, con una placa correctora en su centro de curvatura. Si los radios del secundario y del terciario son de la misma magnitud, pero de signo opuesto, y si el centro de curvatura del terciario se coloca directamente en el vértice del espejo secundario, entonces la placa Schmidt se ubicaría sobre el espejo secundario paraboloide. Por lo tanto, la placa Schmidt requerida para hacer del espejo terciario un telescopio Schmidt se elimina por el paraboloide que figura en el secundario convexo del sistema de Mersenne, ya que cada uno corrige la misma magnitud de aberración esférica, pero de signo opuesto. Además, como el sistema Mersenne + Schmidt es la suma de dos anastigmas (el sistema Mersenne es un anastigma, y también lo es el sistema Schmidt), el sistema resultante también es un anastigma, ya que las aberraciones de tercer orden son puramente aditivas. [2] Además, ahora es más fácil fabricar el secundario. Este diseño también se denomina Mersenne–Schmidt , ya que utiliza una configuración Mersenne como corrector para un telescopio Schmidt.
La solución de Paul tenía un plano focal curvo , pero esto se corrigió en el diseño de Paul-Baker, introducido en 1969 por James Gilbert Baker . [3] El diseño de Paul-Baker agrega espaciado adicional y cambia la forma del secundario a elíptico, lo que corrige la curvatura del campo para aplanar el plano focal. [4]
Dietrich Korsch desarrolló un conjunto más general de soluciones en 1972. [5] Un telescopio Korsch está corregido para la aberración esférica , el coma , el astigmatismo y la curvatura del campo y puede tener un amplio campo de visión al tiempo que garantiza que haya poca luz parásita en el plano focal .


Una variación del diseño Korsch es el telescopio de tres superficies de dos espejos [6] introducido por Shai Eisenberg y Earl T. Pearson en 1987. Empleando las ecuaciones de Korsch con modificaciones mínimas, el número de espejos se reduce de tres a dos combinando la superficie primaria y la superficie terciaria en el mismo espejo. En una opción, la terciaria es idéntica a la primaria, mientras que la segunda opción muestra la terciaria pulida en el espejo primario. El telescopio Eisenberg-Pearson no requiere un espejo plegable plano para permitir el acceso al plano de la imagen ya que el plano focal está ubicado detrás del espejo secundario. Una ilustración compacta del telescopio Korsch publicada en 1995 por Shai Eisenberg [7] es la versión sólida del diseño con el uso de reflexión interna total (TIR) para integrar el cuarto espejo plegable sin introducir viñeteado .