En la teoría de la computación y la teoría de autómatas , la construcción de conjuntos potencia o construcción de subconjuntos es un método estándar para convertir un autómata finito no determinista (AFN) en un autómata finito determinista (AFD) que reconoce el mismo lenguaje formal . Es importante en teoría porque establece que los AFN, a pesar de su flexibilidad adicional, son incapaces de reconocer cualquier lenguaje que no pueda ser reconocido por algún AFD. También es importante en la práctica para convertir AFN más fáciles de construir en AFD ejecutables de manera más eficiente. Sin embargo, si el AFN tiene n estados, el AFD resultante puede tener hasta 2 n estados, un número exponencialmente mayor, lo que a veces hace que la construcción sea poco práctica para AFN grandes.
La construcción, a veces llamada construcción de conjunto de potencias de Rabin-Scott (o construcción de subconjuntos) para distinguirla de construcciones similares para otros tipos de autómatas, fue publicada por primera vez por Michael O. Rabin y Dana Scott en 1959. [1]
Para simular el funcionamiento de un DFA en una cadena de entrada dada, es necesario realizar un seguimiento de un único estado en cualquier momento: el estado al que llegará el autómata después de ver un prefijo de la entrada. En cambio, para simular un NFA, es necesario realizar un seguimiento de un conjunto de estados: todos los estados a los que podría llegar el autómata después de ver el mismo prefijo de la entrada, según las elecciones no deterministas realizadas por el autómata. Si, después de un cierto prefijo de la entrada, se puede alcanzar un conjunto S de estados, entonces después del siguiente símbolo de entrada x el conjunto de estados alcanzables es una función determinista de S y x . Por lo tanto, los conjuntos de estados NFA alcanzables desempeñan el mismo papel en la simulación NFA que los estados DFA individuales en la simulación DFA, y de hecho los conjuntos de estados NFA que aparecen en esta simulación pueden reinterpretarse como estados de un DFA. [2]
La construcción de conjuntos potencia se aplica más directamente a un NFA que no permite transformaciones de estado sin consumir símbolos de entrada (también conocido como: "ε-movimientos"). Un autómata de este tipo puede definirse como una 5-tupla ( Q , Σ , T , q 0 , F ) , en la que Q es el conjunto de estados, Σ es el conjunto de símbolos de entrada, T es la función de transición (que asigna un estado y un símbolo de entrada a un conjunto de estados), q 0 es el estado inicial y F es el conjunto de estados de aceptación. El DFA correspondiente tiene estados que corresponden a subconjuntos de Q . El estado inicial del DFA es { q 0 } , el conjunto (de un elemento) de estados iniciales. La función de transición del DFA asigna un estado S (que representa un subconjunto de Q ) y un símbolo de entrada x al conjunto T ( S , x ) = ∪{ T ( q , x ) | q ∈ S } , el conjunto de todos los estados a los que se puede llegar mediante una transición x desde un estado en S . Un estado S del DFA es un estado de aceptación si y solo si al menos un miembro de S es un estado de aceptación del NFA. [2] [3]
En la versión más simple de la construcción del conjunto potencia, el conjunto de todos los estados del DFA es el conjunto potencia de Q , el conjunto de todos los subconjuntos posibles de Q . Sin embargo, muchos estados del DFA resultante pueden ser inútiles ya que pueden ser inalcanzables desde el estado inicial. Una versión alternativa de la construcción crea solo los estados que son realmente alcanzables. [4]
En el caso de un NFA con ε-movimientos (también llamado ε-NFA), la construcción debe modificarse para abordar estos problemas calculando el ε- cierre de estados: el conjunto de todos los estados alcanzables desde un estado dado utilizando solo ε-movimientos. Van Noord reconoce tres formas posibles de incorporar este cálculo de cierre en la construcción del conjunto potencia: [5]
Si se definen NFA para permitir múltiples estados iniciales, [7] el estado inicial del DFA correspondiente es el conjunto de todos los estados iniciales del NFA, o (si el NFA también tiene ε-movimientos) el conjunto de todos los estados alcanzables desde los estados iniciales mediante ε-movimientos.
El siguiente NFA tiene cuatro estados: el estado 1 es inicial y los estados 3 y 4 son de aceptación. Su alfabeto consta de dos símbolos, 0 y 1, y tiene ε-movimientos.
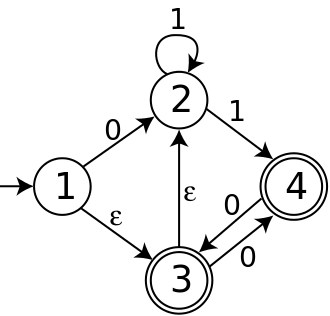
El estado inicial del DFA construido a partir de este NFA es el conjunto de todos los estados del NFA a los que se puede llegar desde el estado 1 mediante ε-movimientos; es decir, es el conjunto {1,2,3}. Una transición desde {1,2,3} mediante el símbolo de entrada 0 debe seguir la flecha del estado 1 al estado 2, o la flecha del estado 3 al estado 4. Además, ni el estado 2 ni el estado 4 tienen ε-movimientos salientes. Por lo tanto, T ({1,2,3},0) = {2,4}, y por el mismo razonamiento el DFA completo construido a partir del NFA es como se muestra a continuación.

Como se puede ver en este ejemplo, hay cinco estados alcanzables desde el estado inicial del DFA; los 11 conjuntos restantes en el conjunto de potencia del conjunto de estados NFA no son alcanzables.

Como los estados DFA consisten en conjuntos de estados NFA, un NFA de n estados puede convertirse en un DFA con como máximo 2 n estados. [2] Para cada n , existen NFA de n estados tales que cada subconjunto de estados es alcanzable desde el subconjunto inicial, de modo que el DFA convertido tiene exactamente 2 n estados, lo que da una complejidad temporal de peor caso de Θ( 2 n ) . [8] [9] Un ejemplo simple que requiere casi esta cantidad de estados es el lenguaje de cadenas sobre el alfabeto {0,1} en el que hay al menos n caracteres, el n -ésimo desde el último de los cuales es 1. Puede representarse mediante un NFA de ( n + 1) estados, pero requiere 2 n estados DFA, uno para cada sufijo de n caracteres de la entrada; cf. imagen para n = 4. [4 ]
El algoritmo de Brzozowski para la minimización de DFA utiliza la construcción de conjuntos de potencias dos veces. Convierte el DFA de entrada en un NFA para el lenguaje inverso, invirtiendo todas sus flechas e intercambiando los roles de los estados inicial y de aceptación, convierte el NFA nuevamente en un DFA utilizando la construcción de conjuntos de potencias y luego repite su proceso. Su complejidad en el peor de los casos es exponencial, a diferencia de otros algoritmos de minimización de DFA conocidos, pero en muchos ejemplos funciona más rápido de lo que su complejidad en el peor de los casos sugeriría. [10]
La construcción de Safra, que convierte un autómata Büchi no determinista con n estados en un autómata Muller determinista o en un autómata Rabin determinista con 2 O( n log n ) estados, utiliza la construcción de conjunto potencia como parte de su maquinaria. [11]