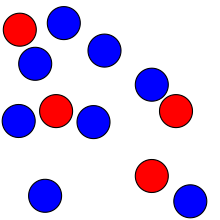
La subitización consiste en realizar juicios rápidos, precisos y seguros sobre números realizados para pequeñas cantidades de elementos. El término fue acuñado en 1949 por EL Kaufman et al., [1] y se deriva del adjetivo latino subitus (que significa "súbito") y captura la sensación de saber inmediatamente cuántos elementos hay dentro de la escena visual, cuando la cantidad de elementos presentes cae dentro del rango de subitización. [1] Los conjuntos de más de cuatro o cinco elementos no se pueden subitizar a menos que los elementos aparezcan en un patrón con el que la persona esté familiarizada (como los seis puntos en una cara de un dado). Los conjuntos grandes y familiares se pueden contar uno por uno (o la persona puede calcular el número a través de un cálculo rápido si puede agrupar mentalmente los elementos en unos pocos conjuntos pequeños). Una persona también podría estimar el número de un conjunto grande, una habilidad similar a la subitización, pero diferente.
La precisión, velocidad y confianza con la que los observadores hacen juicios sobre el número de elementos dependen críticamente del número de elementos que se enumerarán. Los juicios hechos para pantallas compuestas de alrededor de uno a cuatro elementos son rápidos, [2] precisos, [3] y confiables. [4] Sin embargo, una vez que hay más de cuatro elementos para contar, los juicios se hacen con una precisión y confianza decrecientes. [1] Además, los tiempos de respuesta aumentan de manera dramática, con un extra de 250 a 350 ms agregados por cada elemento adicional dentro de la pantalla más allá de aproximadamente cuatro. [5]
Si bien el aumento en el tiempo de respuesta para cada elemento adicional dentro de una pantalla es de 250 a 350 ms por elemento fuera del rango de subitización, todavía hay un aumento significativo, aunque menor, de 40 a 100 ms por elemento dentro del rango de subitización. [2] Se encuentra un patrón similar de tiempos de reacción en niños pequeños, aunque con pendientes más pronunciadas tanto para el rango de subitización como para el rango de enumeración. [6] Esto sugiere que no hay un lapso de aprehensión como tal, si este se define como el número de elementos que pueden ser aprehendidos inmediatamente por los procesos cognitivos, ya que hay un costo adicional asociado con cada elemento adicional enumerado. Sin embargo, las diferencias relativas en los costos asociados con la enumeración de elementos dentro del rango de subitización son pequeñas, ya sea que se midan en términos de precisión, confianza o velocidad de respuesta . Además, los valores de todas las medidas parecen diferir notablemente dentro y fuera del rango de subitización. [1] Por lo tanto, si bien puede no haber un lapso de aprehensión, parece haber diferencias reales en las formas en que el sistema visual procesa una pequeña cantidad de elementos (es decir, aproximadamente cuatro o menos elementos), en comparación con una cantidad mayor de elementos (es decir, aproximadamente más de cuatro elementos).
Un estudio de 2006 demostró que la subitización y el conteo no se limitan a la percepción visual, sino que también se extienden a la percepción táctil, cuando los observadores tenían que nombrar el número de yemas de los dedos estimuladas. [7] Un estudio de 2008 también demostró la subitización y el conteo en la percepción auditiva. [8] Aunque se ha cuestionado la existencia de la subitización en la percepción táctil, [9] este efecto se ha replicado muchas veces y, por lo tanto, puede considerarse robusto. [10] [11] [12] El efecto de subitización también se ha obtenido en la percepción táctil con adultos con ceguera congénita. [13] En conjunto, estos hallazgos respaldan la idea de que la subitización es un mecanismo perceptivo general que se extiende al procesamiento auditivo y táctil.
Como sugiere la derivación del término "subitización", la sensación asociada con la realización de un juicio numérico dentro del rango de subitización es la de estar inmediatamente consciente de los elementos exhibidos. [3] Cuando el número de objetos presentados excede el rango de subitización, esta sensación se pierde y los observadores comúnmente informan una impresión de cambiar su punto de vista alrededor de la exhibición, hasta que se hayan contado todos los elementos presentados. [1] La capacidad de los observadores para contar el número de elementos dentro de una exhibición puede verse limitada, ya sea por la presentación rápida y el enmascaramiento posterior de los elementos, [14] o al requerir que los observadores respondan rápidamente. [1] Ambos procedimientos tienen poco efecto, si es que tienen alguno, en la enumeración dentro del rango de subitización. Estas técnicas pueden restringir la capacidad de los observadores para contar elementos al limitar el grado en el que los observadores pueden cambiar su "zona de atención" [15] sucesivamente a diferentes elementos dentro de la exhibición.
Atkinson, Campbell y Francis [16] demostraron que las imágenes residuales visuales podían emplearse para lograr resultados similares. Utilizando un flash para iluminar una línea de discos blancos, pudieron generar imágenes residuales intensas en observadores adaptados a la oscuridad. Se pidió a los observadores que informaran verbalmente cuántos discos se habían presentado, tanto a los 10 s como a los 60 s después de la exposición del flash. Los observadores informaron que podían ver todos los discos presentados durante al menos 10 s, y que podían percibir al menos algunos de los discos después de 60 s. A diferencia de simplemente mostrar las imágenes durante intervalos de 10 y 60 segundos, cuando se presentan en forma de imágenes residuales, el movimiento ocular no puede emplearse con el propósito de contar: cuando los sujetos mueven los ojos, las imágenes también se mueven. A pesar de que se necesitó un largo período de tiempo para enumerar el número de discos presentados cuando el número de discos presentados se encontraba fuera del rango de subitización (es decir, 5 a 12 discos), los observadores cometieron errores de enumeración consistentes tanto en las condiciones de 10 s como de 60 s. Por el contrario, no se produjeron errores dentro del rango de subitización (es decir, 1 a 4 discos), ni en las condiciones de 10 s ni en las de 60 s. [17]
El trabajo sobre la enumeración de imágenes posteriores [16] [17] apoya la idea de que diferentes procesos cognitivos operan para la enumeración de elementos dentro y fuera del rango de subitización, y como tal plantea la posibilidad de que la subitización y el conteo involucren diferentes circuitos cerebrales. Sin embargo, la investigación de imágenes funcionales ha sido interpretada como que ambos procesos son diferentes [18] y compartidos. [19]
La teoría social que apoya la opinión de que la subitización y el conteo pueden involucrar áreas cerebrales funcional y anatómicamente distintas proviene de pacientes con simultanagnosia , uno de los componentes clave del síndrome de Bálint . [20] Los pacientes con este trastorno sufren una incapacidad para percibir escenas visuales adecuadamente, siendo incapaces de localizar objetos en el espacio, ya sea mirando los objetos, señalándolos o informando verbalmente su posición. [20] A pesar de estos síntomas dramáticos, estos pacientes pueden reconocer correctamente objetos individuales. [21] Crucialmente, las personas con simultanagnosia son incapaces de enumerar objetos fuera del rango de subitización, ya sea no contando ciertos objetos o alternativamente contando el mismo objeto varias veces. [22]
Sin embargo, las personas con simultanagnosia no tienen dificultad para enumerar objetos dentro del rango de subitización. [23] El trastorno está asociado con daño bilateral en el lóbulo parietal , un área del cerebro vinculada con cambios espaciales de atención. [18] Estos resultados neuropsicológicos son consistentes con la visión de que el proceso de contar, pero no el de subitización, requiere cambios activos de atención. Sin embargo, investigaciones recientes han cuestionado esta conclusión al encontrar que la atención también afecta a la subitización. [24]
Otra fuente de investigación sobre los procesos neuronales de subitización en comparación con el conteo proviene de la investigación con tomografía por emisión de positrones (PET) sobre observadores normales. Dicha investigación compara la actividad cerebral asociada con los procesos de enumeración dentro (es decir, 1 a 4 elementos) para la subitización, y fuera (es decir, 5 a 8 elementos) para el conteo. [18] [19]
En este tipo de investigaciones se ha descubierto que, en el intervalo de subitización y conteo, la activación se produce de forma bilateral en la corteza extraestriada occipital y en el lóbulo parietal superior/surco intraparietal. Esto se ha interpretado como una prueba de que intervienen procesos compartidos. [19] Sin embargo, la existencia de activaciones adicionales durante el conteo en las regiones frontales inferiores derechas y en la corteza cingulada anterior se ha interpretado como una indicación de la existencia de procesos distintos durante el conteo relacionados con la activación de regiones implicadas en el cambio de atención. [18]
Históricamente, muchos sistemas han intentado utilizar la subitización para identificar cantidades totales o parciales. En el siglo XX, los docentes de matemáticas comenzaron a adoptar algunos de estos sistemas, como se analiza en los ejemplos a continuación, pero a menudo cambiaron a una codificación de colores más abstracta para representar cantidades hasta diez.
En la década de 1990, se demostró que los bebés de tres semanas de edad diferenciaban entre 1 y 3 objetos, es decir, subitizaban. [22] Un metaestudio más reciente que resumía cinco estudios diferentes concluyó que los bebés nacen con una capacidad innata para diferenciar cantidades dentro de un rango pequeño, que aumenta con el tiempo. [25] A la edad de siete años, esa capacidad aumenta a 4-7 objetos. Algunos profesionales afirman que, con entrenamiento, los niños son capaces de subitizar correctamente más de 15 objetos. [ cita requerida ]
El uso hipotético de la yupana , un sistema de conteo inca, colocaba hasta cinco contadores en bandejas conectadas para realizar los cálculos.
En cada valor posicional, el ábaco chino utiliza cuatro o cinco cuentas para representar unidades, que se subitizan, y una o dos cuentas separadas, que simbolizan los cincos. Esto permite que se realicen operaciones de varios dígitos, como llevar y tomar prestado, sin subitizar más allá del cinco.
Los ábacos europeos utilizan diez cuentas en cada registro, pero normalmente las separan en grupos de cinco por color.
La idea del reconocimiento instantáneo de cantidades ha sido adoptada por varios sistemas pedagógicos, como Montessori , Cuisenaire y Dienes . Sin embargo, estos sistemas solo utilizan parcialmente la subitización, intentando hacer que todas las cantidades del 1 al 10 sean reconocibles instantáneamente. Para lograrlo, codifican las cantidades por color y longitud de varillas o cordones de cuentas que las representan. Reconocer tales representaciones visuales o táctiles y asociar cantidades con ellas implica operaciones mentales diferentes a las de la subitización.
Una de las aplicaciones más básicas es la agrupación de dígitos en números grandes, que permiten saber el tamaño de un vistazo, en lugar de tener que contar. Por ejemplo, escribir un millón (1000000) como 1.000.000 (o 1.000.000 o1 000 000 ) o un billón ( corto ) (1000000000) como 1.000.000.000 (u otras formas, como 1.00.00.00.000 en el sistema de numeración indio ) hace que sea mucho más fácil de leer. Esto es particularmente importante en contabilidad y finanzas, ya que un error de un solo dígito decimal cambia la cantidad por un factor de diez. Esto también se encuentra en los lenguajes de programación de computadoras para valores literales , algunos de los cuales utilizan separadores de dígitos .
Los dados , las cartas y otros dispositivos de juego dividen tradicionalmente las cantidades en grupos subitizables con patrones reconocibles. La ventaja conductual de este método de agrupación ha sido investigada científicamente por Ciccione y Dehaene [26] , quienes demostraron que el desempeño en el conteo mejora si los grupos comparten la misma cantidad de elementos y el mismo patrón repetido.
Una aplicación comparable es dividir representaciones numéricas binarias y hexadecimales, números de teléfono, números de cuentas bancarias (por ejemplo, IBAN , números de seguridad social, matrículas, etc.) en grupos de entre 2 y 5 dígitos separados por espacios, puntos, guiones u otros separadores. Esto se hace para ayudar a supervisar la integridad de un número al compararlo o volver a escribirlo. Esta práctica de agrupar caracteres también facilita la memorización de números grandes y estructuras de caracteres.
Hay al menos un juego que se puede jugar en línea para autoevaluar la propia capacidad para subitizar. [27]