El telémetro estadiamétrico , o método de los estadios , es una técnica de medición de distancias con un instrumento telescópico . El término estadios proviene de una unidad griega de longitud, Stadion (igual a 600 pies griegos, pous ), que era la longitud típica de un estadio deportivo de la época. El telémetro estadiamétrico se utiliza para topografía y en las miras telescópicas de armas de fuego , piezas de artillería o cañones de tanques , así como en algunos binoculares y otros dispositivos ópticos. Todavía se utiliza ampliamente en francotiradores militares de largo alcance , pero en muchas aplicaciones profesionales está siendo reemplazado por métodos de telémetro de microondas , infrarrojos o láser . Aunque son mucho más fáciles de usar, los telémetros electrónicos pueden revelar la posición del tirador a un adversario bien equipado, y la necesidad de una estimación precisa del alcance ha existido durante mucho más tiempo que los telémetros electrónicos pequeños y lo suficientemente resistentes como para ser adecuados para uso militar.

El método de los estadios se basa en el principio de los triángulos semejantes . Esto significa que, para un triángulo con un ángulo dado, la relación entre la longitud del lado opuesto y la longitud del lado adyacente ( tangente [ ancla rota ] ) es constante. Al utilizar una retícula con marcas de un espaciado angular conocido, se puede utilizar el principio de los triángulos semejantes para encontrar la distancia a objetos de tamaño conocido o el tamaño de objetos a una distancia conocida. En cualquier caso, se utiliza el parámetro conocido, junto con la medición angular, para derivar la longitud del otro lado.
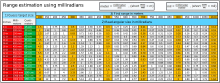
La medición estadiamétrica suele utilizar el milirradián ("mil" o "mrad") como unidad de medida angular. Dado que un radián se define como el ángulo formado cuando la longitud de un arco circular es igual al radio del círculo, un milirradián es el ángulo formado cuando la longitud de un arco circular es igual a 1/1000 del radio del círculo. Para los ángulos telescópicos, las aproximaciones de simplifican enormemente la trigonometría, permitiendo escalar objetos medidos en milirradianes a través de un telescopio por un factor de 1000 para la distancia o la altura. Un objeto de 5 metros de altura, por ejemplo, cubrirá 1 mrad a 5000 metros, o 5 mrad a 1000 metros, o 25 mrad a 200 metros. Dado que el radián expresa una proporción, es independiente de las unidades utilizadas; un objeto de 6 pies de altura que cubra 1 mrad estará a 6000 pies de distancia.
En la práctica, se puede observar que se pueden hacer aproximaciones aproximadas con un triángulo rectángulo cuya base (b) es igual a la distancia del "telémetro" desde el ojo; siendo la abertura (a) el orificio a través del cual se mira el objetivo – el vértice de este triángulo está en la superficie del ojo del usuario.
Para una distancia estándar desde el ojo (b) de 28" (71,12 cm); siendo esta la longitud común del arco de un arquero:
El alcance aproximado de un objeto de un pie (30,48 cm) de altura que cubre aproximadamente 100 miliradianes es de 10 pies (3,048 m) o:
La fórmula anterior funciona para cualquier sistema de medida lineal siempre que r y h se calculen con las mismas unidades.
Las lecturas estadimétricas que se utilizan en topografía se pueden tomar con instrumentos modernos como tránsitos , teodolitos , alidades de plancheta y niveles . Cuando se utiliza el método de medición estadimétrica, se sostiene una vara de nivel o estadimétrica de manera que aparezca entre dos marcas estadimétricas visibles en la retícula del instrumento . La vara estadimétrica tiene medidas escritas en ella que se pueden leer a través del telescopio del instrumento, lo que proporciona una altura remota conocida para los cálculos de distancia.
Un instrumento equipado para trabajar con estadígrafos tiene dos marcas estadimétricas horizontales espaciadas equidistantes del centro de la cruz filar del retículo. El intervalo entre las marcas estadimétricas en la mayoría de los instrumentos topográficos es de 10 mrad y da un factor de intervalo estadimétrico de 100. La distancia entre el instrumento y una vara estadimétrica se puede determinar simplemente multiplicando la medida entre los hilos estadimétricos (conocidos como intervalo estadimétrico) por 100.
El instrumento debe estar nivelado para que este método funcione directamente. Si la línea de visión del instrumento está inclinada con respecto a la mira, se deben determinar los componentes de distancia horizontal y vertical. Algunos instrumentos tienen graduaciones adicionales en un círculo vertical para ayudar con estas mediciones inclinadas. Estos círculos graduados, conocidos como círculos estadimétricos , proporcionan el valor de las mediciones horizontales y verticales como un porcentaje de la medición estadimétrica inclinada.
Este sistema es lo suficientemente preciso para localizar detalles topográficos como ríos, puentes, edificios y carreteras cuando una precisión de 1/500 (0,2 %, 2000 ppm) es aceptable. Las lecturas estadimétricas también se utilizan para proporcionar observaciones repetidas e independientes para mejorar la precisión y proporcionar una verificación de errores para evitar errores en la nivelación .
El método estadimétrico para medir distancias es principalmente histórico para fines topográficos, ya que hoy en día la distancia se mide principalmente con métodos electrónicos o de cinta métrica. Los instrumentos de estación total no tienen líneas estadimétricas marcadas en la retícula. Los métodos tradicionales aún se utilizan en áreas donde los instrumentos modernos no son comunes o por aficionados a los métodos topográficos antiguos.