El coeficiente de masa de aire define la longitud del recorrido óptico directo a través de la atmósfera terrestre , expresado como una relación con la longitud del recorrido verticalmente hacia arriba, es decir, en el cenit . El coeficiente de masa de aire se puede utilizar para ayudar a caracterizar el espectro solar después de que la radiación solar haya viajado a través de la atmósfera.
El coeficiente de masa de aire se utiliza comúnmente para caracterizar el rendimiento de las células solares en condiciones estandarizadas y a menudo se hace referencia a él utilizando la sintaxis "AM" seguida de un número. "AM1.5" es casi universal cuando se caracterizan los paneles de generación de energía terrestre .
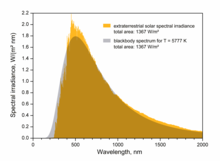
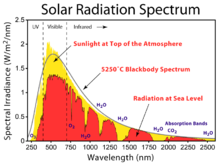
La intensidad total de la radiación solar es similar a la de un radiador de cuerpo negro del mismo tamaño, a unos 5.800 K. [1] A medida que pasa a través de la atmósfera, la luz solar se atenúa por dispersión y absorción ; cuanto más atmósfera atraviese, mayor será la atenuación .
A medida que la luz solar viaja a través de la atmósfera, las sustancias químicas interactúan con ella y absorben ciertas longitudes de onda, modificando la cantidad de luz de longitud de onda corta que llega a la superficie de la Tierra. Un componente más activo de este proceso es el vapor de agua, que genera una amplia variedad de bandas de absorción en muchas longitudes de onda, mientras que el nitrógeno molecular, el oxígeno y el dióxido de carbono contribuyen a este proceso. Cuando llega a la superficie de la Tierra, el espectro está fuertemente limitado entre el infrarrojo lejano y el ultravioleta cercano.
La dispersión atmosférica desempeña un papel en la eliminación de frecuencias más altas de la luz solar directa y su dispersión por el cielo. [2] Es por eso que el cielo se ve azul y el sol amarillo: más luz azul de alta frecuencia llega al observador a través de caminos dispersos indirectos; y menos luz azul sigue el camino directo, lo que le da al sol un tinte amarillo. [3] Cuanto mayor es la distancia en la atmósfera a través de la cual viaja la luz solar, mayor es este efecto, por lo que el sol se ve naranja o rojo al amanecer y al atardecer cuando la luz solar viaja muy oblicuamente a través de la atmósfera: progresivamente, más azules y verdes se eliminan de los rayos directos, lo que le da un aspecto anaranjado o rojo al sol; y el cielo se ve rosa, porque los azules y verdes se dispersan en caminos tan largos que se atenúan mucho antes de llegar al observador, lo que da como resultado cielos rosados característicos al amanecer y al atardecer.
Para una longitud de trayectoria a través de la atmósfera y una radiación solar incidente en un ángulo relativo a la normal a la superficie de la Tierra, el coeficiente de masa de aire es: [4]
donde es la longitud del camino en el cenit (es decir, normal a la superficie de la Tierra) al nivel del mar .
Por lo tanto, el número de masa de aire depende de la trayectoria de elevación del Sol a través del cielo y, por lo tanto, varía con la hora del día, con el paso de las estaciones del año y con la latitud del observador.

Una aproximación de primer orden para la masa de aire viene dada por
donde es el ángulo cenital , normalmente en grados.
La aproximación anterior no tiene en cuenta la altura finita de la atmósfera y predice una masa de aire infinita en el horizonte. Sin embargo, es razonablemente precisa para valores de hasta alrededor de 75°. Se han propuesto varias mejoras para modelar con mayor precisión el espesor de la trayectoria hacia el horizonte, como la propuesta por Kasten y Young (1989): [5]
En el artículo principal Airmass se ofrece una lista más completa de dichos modelos para varios modelos atmosféricos y conjuntos de datos experimentales. A nivel del mar, la masa de aire hacia el horizonte ( = 90°) es de aproximadamente 38. [6]
Modelar la atmósfera como una simple capa esférica proporciona una aproximación razonable: [7]
donde el radio de la Tierra = 6371 km, la altura efectiva de la atmósfera ≈ 9 km y su relación ≈ 708. Para evitar tomar la diferencia de dos números grandes, esto se puede escribir como
lo que también muestra la similitud con la fórmula simple dada anteriormente.
Estos modelos se comparan en la siguiente tabla:
Estos modelos simples suponen que, para estos fines, se puede considerar que la atmósfera está efectivamente concentrada alrededor de los 9 km inferiores, [8] es decir, que esencialmente todos los efectos atmosféricos se deben a la masa atmosférica en la mitad inferior de la troposfera . Este es un modelo útil y simple cuando se consideran los efectos atmosféricos sobre la intensidad solar.
También se puede suponer que la densidad del aire disminuye exponencialmente con la altura. Si x es la distancia que recorre el rayo de luz desde el punto en el que toca el suelo, dividida por el espesor equivalente de la atmósfera (aproximadamente 9 km), entonces la altura de un punto es:
La masa de aire es entonces:
donde es la función de error complementaria . Esto da un valor más bajo, de alrededor de 33, cuando el sol está en el horizonte. Sin embargo, ni este modelo ni el anterior tienen en cuenta la curvatura de los rayos de luz debido a la refracción (véase Nivelación ). Un modelo más realista se basaría en la fórmula barométrica para la densidad.
El espectro que se encuentra fuera de la atmósfera se denomina "AM0", es decir, "atmósferas cero". Las células solares que se utilizan para aplicaciones de energía espacial, como las de los satélites de comunicaciones , se caracterizan generalmente utilizando AM0.
El espectro después de atravesar la atmósfera hasta el nivel del mar con el sol directamente sobre él se denomina, por definición, "AM1", es decir, "una atmósfera". AM1 ( =0°) a AM1.1 ( =25°) es un rango útil para estimar el rendimiento de las células solares en las regiones ecuatoriales y tropicales .
Los paneles solares no suelen funcionar con un espesor de una atmósfera exactamente: si el sol está en un ángulo con respecto a la superficie de la Tierra, el espesor efectivo será mayor. Muchos de los principales centros de población del mundo, y por lo tanto de las instalaciones e industrias solares, en Europa, China, Japón, Estados Unidos de América y otros lugares (incluido el norte de la India, el sur de África y Australia) se encuentran en latitudes templadas . Por lo tanto, es mucho más común un número AM que represente el espectro en latitudes medias.
"AM1.5", con un espesor de 1,5 atmósferas, corresponde a un ángulo cenital solar de =48,2°. Si bien el número AM de verano para latitudes medias durante las partes centrales del día es menor que 1,5, se aplican cifras más altas por la mañana y por la tarde y en otros momentos del año. Por lo tanto, AM1.5 es útil para representar el promedio anual general para latitudes medias. El valor específico de 1,5 se ha seleccionado en la década de 1970 con fines de normalización, con base en un análisis de datos de irradiancia solar en los Estados Unidos limítrofes. [9] Desde entonces, la industria solar ha estado utilizando AM1.5 para todas las pruebas o clasificaciones estandarizadas de células o módulos solares terrestres, incluidos los utilizados en sistemas de concentración. Las últimas normas AM1.5 relacionadas con aplicaciones fotovoltaicas son ASTM G-173 [10] [11] e IEC 60904, todas derivadas de simulaciones obtenidas con el código SMARTS .
La iluminancia para luz diurna ( esta versión ) bajo AM1.5 se da como 109.870 lux (que corresponde al espectro AM1.5 a 1000,4 W/m2 ) .
AM2 ( =60°) a AM3 ( =70°) es un rango útil para estimar el rendimiento promedio general de las células solares instaladas en latitudes altas, como en el norte de Europa. De manera similar, AM2 a AM3 es útil para estimar el rendimiento en invierno en latitudes templadas, por ejemplo, el coeficiente de masa de aire es mayor que 2 a todas las horas del día en invierno en latitudes tan bajas como 37°.
Generalmente se considera que AM38 es la masa de aire en dirección horizontal ( =90°, es decir, la puesta del sol) al nivel del mar. [6] Sin embargo, en la práctica existe un alto grado de variabilidad en la intensidad solar recibida en ángulos cercanos al horizonte, como se describe en la siguiente sección Intensidad solar.
La masa de aire relativa es sólo una función del ángulo cenital del sol y, por lo tanto, no cambia con la elevación local. Por el contrario, la masa de aire absoluta , igual a la masa de aire relativa multiplicada por la presión atmosférica local y dividida por la presión estándar (a nivel del mar), disminuye con la elevación sobre el nivel del mar. Para paneles solares instalados a grandes altitudes, por ejemplo, en una región del Altiplano , es posible utilizar un número de AM absoluto más bajo que para la latitud correspondiente al nivel del mar: números de AM menores a 1 hacia el ecuador y, en consecuencia, números más bajos que los enumerados anteriormente para otras latitudes. Sin embargo, este enfoque es aproximado y no se recomienda. Es mejor simular el espectro real en función de la masa de aire relativa (por ejemplo, 1,5) y las condiciones atmosféricas reales para la elevación específica del sitio bajo escrutinio.
La intensidad solar en el colector se reduce con el aumento del coeficiente de masa de aire, pero debido a los complejos y variables factores atmosféricos involucrados, no de una manera simple o lineal. Por ejemplo, casi toda la radiación de alta energía se elimina en la atmósfera superior (entre AM0 y AM1) y, por lo tanto, AM2 no es el doble de mala que AM1. Además, existe una gran variabilidad en muchos de los factores que contribuyen a la atenuación atmosférica, [12] como el vapor de agua, los aerosoles, el smog fotoquímico y los efectos de las inversiones de temperatura . Dependiendo del nivel de contaminación en el aire, la atenuación general puede cambiar hasta en un ±70% hacia el horizonte, lo que afecta en gran medida el rendimiento, particularmente hacia el horizonte, donde los efectos de las capas inferiores de la atmósfera se amplifican muchas veces.
Un modelo de aproximación empírica para la intensidad solar versus la masa de aire viene dado por: [13] [14]
donde la intensidad solar externa a la atmósfera de la Tierra = 1,353 kW/m 2 , y el factor de 1,1 se deriva asumiendo que el componente difuso es el 10% del componente directo. [13]
Esta fórmula se ajusta cómodamente dentro del rango medio de la variabilidad esperada basada en la contaminación:
Esto demuestra que sólo unos pocos grados por encima del horizonte pueden proporcionar una potencia significativa. Por ejemplo, cuando el sol se encuentra a más de 60° por encima del horizonte ( <30°), la intensidad solar es de unos 1000 W/m2 ( según la ecuación I.1, como se muestra en la tabla anterior), mientras que cuando el sol se encuentra a sólo 15° por encima del horizonte ( =75°), la intensidad solar sigue siendo de unos 600 W/m2 , o el 60% de su nivel máximo; y a sólo 5° por encima del horizonte sigue siendo el 27% del máximo.
Un modelo aproximado para el aumento de intensidad con la altitud y con una precisión de unos pocos kilómetros sobre el nivel del mar viene dado por: [13] [19]
donde es la altura del colector solar sobre el nivel del mar en km y es la masa de aire (de A.2 ) como si el colector estuviera instalado a nivel del mar.
Alternativamente, dadas las importantes variabilidades prácticas involucradas, el modelo esférico homogéneo podría aplicarse para estimar AM, utilizando:
donde las alturas normalizadas de la atmósfera y del colector son respectivamente ≈ 708 (como arriba) y .
Y luego la tabla anterior o la ecuación apropiada ( I.1 o I.3 o I.4 para aire promedio, contaminado o limpio respectivamente) se puede utilizar para estimar la intensidad de AM de la manera normal.
Estas aproximaciones en I.2 y A.4 son adecuadas para su uso sólo a altitudes de unos pocos kilómetros sobre el nivel del mar, lo que implica una reducción a los niveles de rendimiento AM0 sólo a unos 6 y 9 km respectivamente. Por el contrario, gran parte de la atenuación de los componentes de alta energía se produce en la capa de ozono, a altitudes superiores de unos 30 km. [20] Por lo tanto, estas aproximaciones sólo son adecuadas para estimar el rendimiento de los colectores terrestres.
La atmósfera de la Tierra absorbe una cantidad considerable de luz ultravioleta. El espectro resultante en la superficie de la Tierra tiene menos fotones, pero son de menor energía en promedio, por lo que el número de fotones, por encima de la banda prohibida , por unidad de energía solar es mayor que en el espacio. Esto significa que las células solares son más eficientes en AM1 que en AM0. Este resultado aparentemente contra-intuitivo surge simplemente porque las células de silicio no pueden hacer mucho uso de la radiación de alta energía que filtra la atmósfera. Como se ilustra a continuación, aunque la eficiencia es menor en AM0, la potencia de salida total ( Pout ) para una célula solar típica sigue siendo más alta en AM0. Por el contrario, la forma del espectro no cambia significativamente con mayores aumentos en el espesor atmosférico y, por lo tanto, la eficiencia de la célula no cambia mucho para números de AM superiores a 1.
Esto ilustra el punto más general de que, dado que la energía solar es "gratuita", y donde el espacio disponible no es una limitación, otros factores como la potencia de salida total P out y P out por unidad de dinero invertido (por ejemplo, por dólar), son a menudo consideraciones más importantes que la eficiencia ( P out /P in ).