
En el análisis numérico, la escalada de pendientes es una técnica de optimización matemática que pertenece a la familia de la búsqueda local . Es un algoritmo iterativo que comienza con una solución arbitraria para un problema y luego intenta encontrar una mejor solución haciendo un cambio incremental en la solución. Si el cambio produce una mejor solución, se realiza otro cambio incremental en la nueva solución, y así sucesivamente hasta que no se puedan encontrar más mejoras.
Por ejemplo, la escalada de colinas se puede aplicar al problema del viajante de comercio . Es fácil encontrar una solución inicial que visite todas las ciudades, pero es probable que sea muy deficiente en comparación con la solución óptima. El algoritmo comienza con una solución de este tipo y le hace pequeñas mejoras, como cambiar el orden en el que se visitan dos ciudades. Al final, es probable que se obtenga una ruta mucho más corta.
La escalada de colinas encuentra soluciones óptimas para problemas convexos ; para otros problemas, solo encontrará óptimos locales (soluciones que no se pueden mejorar con ninguna configuración vecina), que no son necesariamente la mejor solución posible (el óptimo global ) de todas las soluciones posibles (el espacio de búsqueda ). Los ejemplos de algoritmos que resuelven problemas convexos mediante escalada de colinas incluyen el algoritmo simplex para programación lineal y búsqueda binaria . [1] : 253 Para intentar evitar quedarse atascado en óptimos locales, se podrían usar reinicios (es decir, búsqueda local repetida), o esquemas más complejos basados en iteraciones (como la búsqueda local iterada ), o en memoria (como la optimización de búsqueda reactiva y la búsqueda tabú ), o en modificaciones estocásticas sin memoria (como el recocido simulado ).
La relativa simplicidad del algoritmo lo convierte en una opción popular entre los algoritmos de optimización. Se utiliza ampliamente en inteligencia artificial para alcanzar un estado objetivo desde un nodo de inicio. En algoritmos relacionados se utilizan diferentes opciones para los siguientes nodos y los nodos de inicio. Aunque algoritmos más avanzados como el recocido simulado o la búsqueda tabú pueden dar mejores resultados, en algunas situaciones la escalada de pendientes funciona igual de bien. La escalada de pendientes a menudo puede producir un mejor resultado que otros algoritmos cuando la cantidad de tiempo disponible para realizar una búsqueda es limitada, como en los sistemas en tiempo real, siempre que una pequeña cantidad de incrementos converja típicamente en una buena solución (la solución óptima o una aproximación cercana). En el otro extremo, la ordenación de burbuja puede verse como un algoritmo de escalada de pendientes (cada intercambio de elementos adyacentes disminuye la cantidad de pares de elementos desordenados), pero este enfoque está lejos de ser eficiente incluso para N modestos, ya que la cantidad de intercambios necesarios crece cuadráticamente.
El ascenso de pendientes es un algoritmo que funciona en cualquier momento : puede devolver una solución válida incluso si se interrumpe en cualquier momento antes de finalizar.
El método de escalada de colinas intenta maximizar (o minimizar) una función objetivo , donde es un vector de valores continuos y/o discretos. En cada iteración, el método de escalada de colinas ajustará un único elemento en y determinará si el cambio mejora el valor de . (Tenga en cuenta que esto difiere de los métodos de descenso de gradiente , que ajustan todos los valores en en cada iteración de acuerdo con el gradiente de la colina). Con el método de escalada de colinas, se acepta cualquier cambio que mejore y el proceso continúa hasta que no se pueda encontrar ningún cambio que mejore el valor de . Entonces se dice que es "localmente óptimo".
En espacios vectoriales discretos, cada valor posible de se puede visualizar como un vértice en un gráfico . La pendiente seguirá el gráfico de vértice a vértice, siempre aumentando (o disminuyendo) localmente el valor de , hasta que se alcance un máximo local (o un mínimo local ) .
En la escalada de colinas simple , se elige el primer nodo más cercano, mientras que en la escalada de colinas con ascenso más empinado se comparan todos los sucesores y se elige el más cercano a la solución. Ambas formas fallan si no hay un nodo más cercano, lo que puede suceder si hay máximos locales en el espacio de búsqueda que no son soluciones. La escalada de colinas con ascenso más empinado es similar a la búsqueda del mejor primero , que prueba todas las extensiones posibles de la ruta actual en lugar de solo una. [2]
El método estocástico de ascenso de colinas no examina a todos los vecinos antes de decidir cómo mudarse, sino que selecciona un vecino al azar y decide (según el grado de mejora de ese vecino) si mudarse a ese vecino o examinar a otro.
El descenso de coordenadas realiza una búsqueda lineal a lo largo de una dirección de coordenadas en el punto actual en cada iteración. Algunas versiones del descenso de coordenadas eligen aleatoriamente una dirección de coordenadas diferente en cada iteración.
El ascenso de colinas con reinicio aleatorio es un metaalgoritmo construido sobre el algoritmo de ascenso de colinas. También se lo conoce como ascenso de colinas Shotgun . Realiza el ascenso de colinas de forma iterativa, cada vez con una condición inicial aleatoria . Se conserva lo mejor : si una nueva ejecución del ascenso de colinas produce un resultado mejor que el estado almacenado, reemplaza el estado almacenado.
El reinicio aleatorio de una pendiente es un algoritmo sorprendentemente eficaz en muchos casos. Resulta que a menudo es mejor dedicar tiempo de CPU a explorar el espacio que optimizar cuidadosamente a partir de una condición inicial. [¿ Investigación original? ]
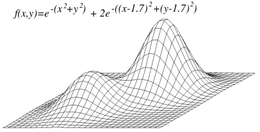
El método de escalada de pendientes no necesariamente encontrará el máximo global, sino que puede converger en un máximo local . Este problema no ocurre si la heurística es convexa. Sin embargo, como muchas funciones no son convexas, el método de escalada de pendientes a menudo puede no alcanzar un máximo global. Otros algoritmos de búsqueda local intentan superar este problema, como el método de escalada de pendientes estocástico , los recorridos aleatorios y el recocido simulado .
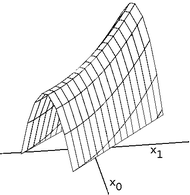
Las crestas son un problema complicado para los escaladores de colinas que optimizan en espacios continuos. Debido a que los escaladores de colinas solo ajustan un elemento en el vector a la vez, cada paso se moverá en una dirección alineada con el eje. Si la función objetivo crea una cresta angosta que asciende en una dirección no alineada con el eje (o si el objetivo es minimizar, un callejón angosto que desciende en una dirección no alineada con el eje), entonces el escalador de colinas solo puede ascender la cresta (o descender el callejón) en zigzag. Si los lados de la cresta (o callejón) son muy empinados, entonces el escalador de colinas puede verse obligado a dar pasos muy pequeños mientras zigzaguea hacia una mejor posición. Por lo tanto, puede llevar un tiempo irrazonable para que ascienda la cresta (o descienda el callejón).
Por el contrario, los métodos de descenso de gradiente pueden moverse en cualquier dirección en la que la cresta o el callejón puedan ascender o descender. Por lo tanto, el descenso de gradiente o el método de gradiente conjugado generalmente se prefieren al método de ascenso de colinas cuando la función objetivo es diferenciable. Sin embargo, los métodos de ascenso de colinas tienen la ventaja de no requerir que la función objetivo sea diferenciable, por lo que los métodos de ascenso de colinas pueden ser preferidos cuando la función objetivo es compleja.
Otro problema que a veces ocurre con el ascenso de pendientes es el de las mesetas. Se producen mesetas cuando el espacio de búsqueda es plano o lo suficientemente plano como para que el valor devuelto por la función de destino sea indistinguible del valor devuelto para las regiones cercanas debido a la precisión que utiliza la máquina para representar su valor. En tales casos, el escalador de pendientes puede no ser capaz de determinar en qué dirección debe avanzar y puede desviarse en una dirección que nunca conduce a una mejora.
Algoritmo de pseudocódigo Discrete Space Hill Climbing es nodoActual := nodoInicio hacer bucle L := VECINOS(NodoActual) siguienteEval := −INF siguienteNodo := NULL para todo x en L hacer si EVAL(x) > nextEval entonces siguienteNodo := x siguienteEval := EVAL(x) si nextEval ≤ EVAL(nodoActual) entonces // Devuelve el nodo actual ya que no existen mejores vecinos Devuelve el nodo actual nodoActual := nodoSiguiente
Algoritmo de escalada espacial continua currentPoint := initialPoint // el vector de magnitud cero es común stepSize := initialStepSizes // un vector de todos los 1 es común aceleración := algunaAceleración // un valor como 1.2 es común candidato[0] := −aceleración candidato[1] := −1 / aceleración candidato[2] := 1 / aceleración candidato[3] := aceleración mejorPuntaje := EVAL(PuntoActual) hacer bucle antes dePuntuación := mejorPuntuación Para cada elemento i en currentPoint hacer antes dePunto := PuntoActual[i] mejorPaso := 0 para j de 0 a 3 haga // pruebe cada una de las 4 ubicaciones candidatas paso := tamañoDePaso[i] × candidato[j] currentPoint[i] := beforePoint + paso puntuación := EVAL(puntoActual) Si la puntuación > mejorPuntuación entonces mejorPuntuación := puntuación mejorPaso := paso Si bestStep es 0 entonces puntoActual[i] := puntoAntes stepSize[i] := stepSize[i] / aceleración demás PuntoActual[i] := PuntoAntes + mejorPaso stepSize[i] := bestStep // aceleración si (bestScore − beforeScore) < epsilon entonces devuelve currentPoint
Algoritmo genético de contraste ; optimización aleatoria .