La selección de materiales es un paso en el proceso de diseño de cualquier objeto físico. En el contexto del diseño de productos , el objetivo principal de la selección de materiales es minimizar los costos y cumplir con los objetivos de rendimiento del producto. [1] La selección sistemática del mejor material para una aplicación determinada comienza con las propiedades y los costos de los materiales candidatos. La selección de materiales a menudo se beneficia mediante el uso del índice de material o índice de rendimiento relevante para las propiedades deseadas del material. [2] Por ejemplo, una manta térmica debe tener una conductividad térmica deficiente para minimizar la transferencia de calor para una diferencia de temperatura dada. Es esencial que un diseñador tenga un conocimiento profundo de las propiedades de los materiales y su comportamiento en condiciones de trabajo. Algunas de las características importantes de los materiales son: resistencia, durabilidad, flexibilidad, peso, resistencia al calor y la corrosión, capacidad de fundición, soldadura o endurecimiento, maquinabilidad, conductividad eléctrica, etc. [3] En el diseño contemporáneo, la sustentabilidad es una consideración clave en la selección de materiales. [4] La creciente conciencia ambiental impulsa a los profesionales a priorizar factores como el impacto ecológico, la reciclabilidad y el análisis del ciclo de vida en su proceso de toma de decisiones.
La selección sistemática para aplicaciones que requieren múltiples criterios es más compleja. Por ejemplo, cuando el material debe ser rígido y liviano, para una varilla, una combinación de un módulo de Young alto y una densidad baja indica el mejor material, mientras que para una placa, la raíz cúbica de la rigidez dividida por la densidad es el mejor indicador, ya que la rigidez a la flexión de una placa se escala por su espesor al cubo. De manera similar, nuevamente considerando tanto la rigidez como la ligereza, para una varilla que se tirará en tensión, se debe considerar el módulo específico , o el módulo dividido por la densidad , mientras que para una viga que estará sujeta a flexión, el índice del material es el mejor indicador.
La realidad presenta a menudo limitaciones y hay que tener en cuenta el factor utilitario. El coste del material ideal, según su forma, tamaño y composición, puede ser prohibitivo y la demanda, la frecuencia de uso de los artículos más conocidos, sus características e incluso la región del mercado determinan su disponibilidad.
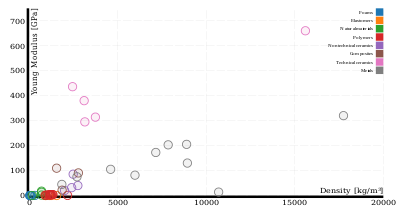
Un diagrama de Ashby, llamado así por Michael Ashby de la Universidad de Cambridge , es un diagrama de dispersión que muestra dos o más propiedades de muchos materiales o clases de materiales. [5] Estos gráficos son útiles para comparar la relación entre diferentes propiedades. Para el ejemplo de la parte rígida/liviana discutida anteriormente, tendría el módulo de Young en un eje y la densidad en el otro eje, con un punto de datos en el gráfico para cada material candidato. En un gráfico de este tipo, es fácil encontrar no solo el material con la mayor rigidez, o con la menor densidad, sino también el que tiene la mejor relación . El uso de una escala logarítmica en ambos ejes facilita la selección del material con la mejor rigidez de placa .
El primer gráfico de la derecha muestra la densidad y el módulo de Young en una escala lineal. El segundo gráfico muestra los mismos atributos de los materiales en una escala logarítmica. Las familias de materiales (polímeros, espumas, metales, etc.) se identifican mediante colores.
El costo de los materiales juega un papel muy importante en su selección. La forma más sencilla de ponderar el costo frente a las propiedades es desarrollar una métrica monetaria para las propiedades de las piezas. Por ejemplo, la evaluación del ciclo de vida puede mostrar que el valor actual neto de reducir el peso de un automóvil en 1 kg es de alrededor de $5 en promedio, por lo que la sustitución de materiales que reduce el peso de un automóvil puede costar hasta $5 más por kilogramo de reducción de peso que el material original. [ cita requerida ] Sin embargo, la dependencia geográfica y temporal de la energía, el mantenimiento y otros costos operativos, y la variación en las tasas de descuento y los patrones de uso (distancia recorrida por año en este ejemplo) entre individuos, significa que no hay una única cifra correcta para esto. Para los aviones comerciales, esta cifra está más cerca de $450/kg, y para las naves espaciales, los costos de lanzamiento de alrededor de $20.000/kg dominan las decisiones de selección. [6]
Así, a medida que los precios de la energía han aumentado y la tecnología ha mejorado, los automóviles han sustituido cantidades cada vez mayores de acero por aleaciones ligeras de magnesio y aluminio , los aviones están sustituyendo el aluminio por plástico reforzado con fibra de carbono y aleaciones de titanio , y los satélites se han fabricado desde hace mucho tiempo con materiales compuestos exóticos .
Por supuesto, el costo por kg no es el único factor importante en la selección de materiales. Un concepto importante es el "costo por unidad de función". Por ejemplo, si el objetivo clave del diseño fuera la rigidez de una placa del material, como se describe en el párrafo introductorio anterior, entonces el diseñador necesitaría un material con la combinación óptima de densidad, módulo de Young y precio. Optimizar combinaciones complejas de propiedades técnicas y de precio es un proceso difícil de lograr manualmente, por lo que el software de selección racional de materiales es una herramienta importante.
El uso de un "diagrama de Ashby" es un método habitual para elegir el material adecuado. En primer lugar, se identifican tres conjuntos diferentes de variables:
A continuación, se deriva una ecuación para el índice de rendimiento . Esta ecuación cuantifica numéricamente cuán deseable será el material para una situación específica. Por convención, un índice de rendimiento más alto denota un mejor material. Por último, el índice de rendimiento se representa gráficamente en el diagrama de Ashby. La inspección visual revela el material más deseable.
En este ejemplo, el material estará sujeto tanto a tensión como a flexión . Por lo tanto, el material óptimo tendrá un buen rendimiento en ambas circunstancias.
En la primera situación, la viga experimenta dos fuerzas: el peso de la gravedad y la tensión . Las variables del material son la densidad y la resistencia . Supongamos que la longitud y la tensión son fijas, lo que las convierte en variables de diseño. Por último, el área de la sección transversal es una variable libre. El objetivo en esta situación es minimizar el peso eligiendo un material con la mejor combinación de variables del material . La figura 1 ilustra esta carga.
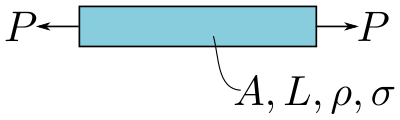
La tensión en la viga se mide como mientras que el peso se describe por . Para obtener un índice de rendimiento es necesario eliminar todas las variables libres, dejando solo las variables de diseño y las variables de material. En este caso, eso significa que se deben eliminar. La ecuación de tensión axial se puede reorganizar para obtener . Sustituyendo esto en la ecuación de peso se obtiene . A continuación, las variables de material y las variables de diseño se agrupan por separado, lo que da .
Dado que tanto y son fijos, y dado que el objetivo es minimizar , entonces la relación debe minimizarse. Sin embargo, por convención, el índice de rendimiento siempre es una cantidad que debe maximizarse. Por lo tanto, la ecuación resultante es
A continuación, supongamos que el material también está sometido a fuerzas de flexión. La ecuación de esfuerzo de tracción máximo de flexión es , donde es el momento de flexión , es la distancia desde el eje neutro y es el momento de inercia. Esto se muestra en la Figura 2. Utilizando la ecuación de peso anterior y resolviendo para las variables libres, la solución a la que se llega es , donde es la longitud y es la altura de la viga. Suponiendo que , , y son variables de diseño fijas, el índice de rendimiento para la flexión se convierte en .
En este punto se han derivado dos índices de rendimiento: para tensión y para flexión . El primer paso es crear un gráfico logarítmico y agregar todos los materiales conocidos en las ubicaciones adecuadas. Sin embargo, las ecuaciones del índice de rendimiento deben modificarse antes de representarlas en el gráfico logarítmico.
Para la ecuación de rendimiento de tensión , el primer paso es tomar el logaritmo de ambos lados. La ecuación resultante se puede reorganizar para dar . Tenga en cuenta que esto sigue el formato de , lo que lo hace lineal en un gráfico logarítmico-logarítmico. De manera similar, la intersección con y es el logaritmo de . Por lo tanto, el valor fijo de para la tensión en la Figura 3 es 0,1.
La ecuación de rendimiento de flexión se puede tratar de manera similar. Utilizando la propiedad de potencia de los logaritmos se puede derivar que . El valor de para la flexión es ≈ 0,0316 en la Figura 3. Finalmente, ambas líneas se trazan en el diagrama de Ashby.
En primer lugar, los mejores materiales de flexión se pueden encontrar examinando qué regiones están más arriba en el gráfico que la línea de flexión. En este caso, algunas de las espumas (azul) y cerámicas técnicas (rosa) están más arriba que la línea. Por lo tanto, esos serían los mejores materiales de flexión. Por el contrario, los materiales que están muy por debajo de la línea (como los metales en la parte inferior derecha de la región gris) serían los peores materiales.
Por último, la línea de tensión se puede utilizar para "romper el empate" entre las espumas y las cerámicas técnicas. Dado que las cerámicas técnicas son el único material que se encuentra por encima de la línea de tensión, los materiales de tensión con mejor rendimiento son las cerámicas técnicas. Por lo tanto, el mejor material en general es una cerámica técnica en la parte superior izquierda de la región rosa, como el carburo de boro .
El índice de rendimiento se puede representar gráficamente en el diagrama de Ashby convirtiendo la ecuación a una escala logarítmica. Esto se hace tomando el logaritmo de ambos lados y representándolo de manera similar a una línea con la intersección en el eje y. Esto significa que cuanto mayor sea la intersección, mayor será el rendimiento del material. Al mover la línea hacia arriba en el diagrama de Ashby, el índice de rendimiento aumenta. Cada material por el que pasa la línea tiene el índice de rendimiento indicado en el eje y. Por lo tanto, al moverse hacia la parte superior del gráfico mientras se sigue tocando una región del material es donde se encontrará el rendimiento más alto.
Como se puede ver en la figura 3, las dos líneas se interceptan cerca de la parte superior del gráfico en las cerámicas técnicas y los materiales compuestos. Esto dará un índice de rendimiento de 120 para carga de tracción y 15 para flexión. Si tenemos en cuenta el coste de las cerámicas de ingeniería, especialmente porque la intersección está alrededor del carburo de boro, este no sería el caso óptimo. Un mejor caso con un índice de rendimiento más bajo pero soluciones más rentables es alrededor de los materiales compuestos de ingeniería cerca del CFRP.
Medios relacionados con Selección de materiales en Wikimedia Commons![{\displaystyle {\sqrt[{3}]{E}}/\rho }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c59e1821d68e3209f3e80363bf7cb0aa9a67aa2)
![{\displaystyle {\sqrt[{2}]{E}}/\rho }](https://wikimedia.org/api/rest_v1/media/math/render/svg/405953ee2761b552e70a0498ca72e95e0d5a84a2)
