Isostasia

Estado de equilibrio gravitacional entre la corteza y el manto terrestre

La isostasia (del griego ísos 'igual', stásis 'inmóvil') o equilibrio isostático es el estado de equilibrio gravitacional entre la corteza terrestre (o litosfera ) y el manto , de modo que la corteza "flota" a una altura que depende de su espesor y densidad. Este concepto se invoca para explicar cómo pueden existir diferentes alturas topográficas en la superficie de la Tierra. Aunque originalmente se definió en términos de corteza continental y manto, ^[1] posteriormente se ha interpretado en términos de litosfera y astenosfera , particularmente con respecto a los volcanes de islas oceánicas , ^[2] como las islas hawaianas .

Aunque la Tierra es un sistema dinámico que responde a las cargas de muchas maneras diferentes, ^[3] la isostasia describe el importante caso límite en el que la corteza y el manto están en equilibrio estático . Ciertas áreas (como el Himalaya y otros márgenes convergentes) no están en equilibrio isostático y no están bien descritas por los modelos isostáticos.

El término general isostasia fue acuñado en 1882 por el geólogo estadounidense Clarence Dutton . ^{[4] [5] [6]}

Historia del concepto

En los siglos XVII y XVIII, los geodesistas franceses (por ejemplo, Jean Picard ) intentaron determinar la forma de la Tierra (el geoide ) midiendo la longitud de un grado de latitud en diferentes latitudes ( medición de arco ). Un grupo que trabajaba en Ecuador sabía que sus líneas de plomada , utilizadas para determinar la dirección vertical, se desviarían por la atracción gravitatoria de las cercanas montañas de los Andes . Sin embargo, la desviación fue menor de lo esperado, lo que se atribuyó a que las montañas tenían raíces de baja densidad que compensaban la masa de las montañas. En otras palabras, las raíces de montaña de baja densidad proporcionaban la flotabilidad para soportar el peso de las montañas sobre el terreno circundante. Observaciones similares en el siglo XIX por topógrafos británicos en la India mostraron que este era un fenómeno generalizado en las áreas montañosas. Más tarde se descubrió que la diferencia entre el campo gravitacional local medido y lo que se esperaba para la altitud y el terreno local (la anomalía de Bouguer ) es positiva sobre las cuencas oceánicas y negativa sobre las áreas continentales altas. Esto demuestra que la baja elevación de las cuencas oceánicas y la alta elevación de los continentes también se compensan en profundidad. ^[7]

El geólogo estadounidense Clarence Dutton utilizó la palabra "isostasia" en 1889 para describir este fenómeno general. ^{[4] [5] [6]} Sin embargo, para entonces ya se habían propuesto dos hipótesis para explicar el fenómeno, en 1855, una por George Airy y la otra por John Henry Pratt . ^[8] La hipótesis de Airy fue refinada más tarde por el geodesista finlandés Veikko Aleksanteri Heiskanen y la hipótesis de Pratt por el geodesista estadounidense John Fillmore Hayford . ^[3]

Tanto la hipótesis de Airy-Heiskanen como la de Pratt-Hayford suponen que la isostasia refleja un equilibrio hidrostático local. Una tercera hipótesis, la flexión litosférica , tiene en cuenta la rigidez de la capa exterior de la Tierra, la litosfera . ^[9] La flexión litosférica se invocó por primera vez a fines del siglo XIX para explicar las líneas costeras elevadas en Escandinavia después del derretimiento de los glaciares continentales al final de la última glaciación . También fue utilizada por el geólogo estadounidense GK Gilbert para explicar las líneas costeras elevadas del lago Bonneville . ^[10] El concepto fue desarrollado aún más en la década de 1950 por el geodesista holandés Vening Meinesz . ^[3]

Modelos

Se utilizan tres modelos principales de isostasia: ^{[3] [11]}

1. El modelo de Airy-Heiskanen, en el que las diferentes alturas topográficas se adaptan a los cambios en el espesor de la corteza , en el que la corteza tiene una densidad constante.
2. El modelo Pratt-Hayford, donde diferentes alturas topográficas se adaptan a los cambios laterales en la densidad de la roca .
3. El modelo de Vening Meinesz, o modelo de isostasia flexural, donde la litosfera actúa como una placa elástica y su rigidez inherente distribuye las cargas topográficas locales sobre una amplia región mediante flexión.

La isostasia de Airy y Pratt son afirmaciones de flotabilidad, pero la isostasia de flexión es una afirmación de flotabilidad cuando se desvía una lámina de resistencia elástica finita. En otras palabras, los modelos de Airy y Pratt son puramente hidrostáticos y no tienen en cuenta la resistencia del material, mientras que la isostasia de flexión tiene en cuenta las fuerzas elásticas de la deformación de la corteza rígida. Estas fuerzas elásticas pueden transmitir fuerzas de flotabilidad a través de una gran región de deformación a una carga más concentrada.

El equilibrio isostático perfecto solo es posible si el material del manto está en reposo. Sin embargo, en el manto hay convección térmica , lo que introduce fuerzas viscosas que no se tienen en cuenta en la teoría estática de la isostasia. La anomalía isostática o IA se define como la anomalía de Bouger menos la anomalía de gravedad debida a la compensación del subsuelo, y es una medida de la desviación local del equilibrio isostático. En el centro de una meseta nivelada, es aproximadamente igual a la anomalía del aire libre . ^[12] Los modelos como la isostasia dinámica profunda (DDI) incluyen dichas fuerzas viscosas y son aplicables a un manto y litosfera dinámicos. ^[13] Las mediciones de la tasa de rebote isostático (el retorno al equilibrio isostático tras un cambio en la carga de la corteza) proporcionan información sobre la viscosidad del manto superior. ^[14]

Aireado

Isostasia aérea, en la que una corteza de densidad constante flota sobre un manto de mayor densidad y la topografía está determinada por el espesor de la corteza.

Isostasia de Airy aplicada a un escenario de cuenca de caso real, donde la carga total sobre el manto está compuesta por un basamento cortical, sedimentos de menor densidad y agua marina suprayacente

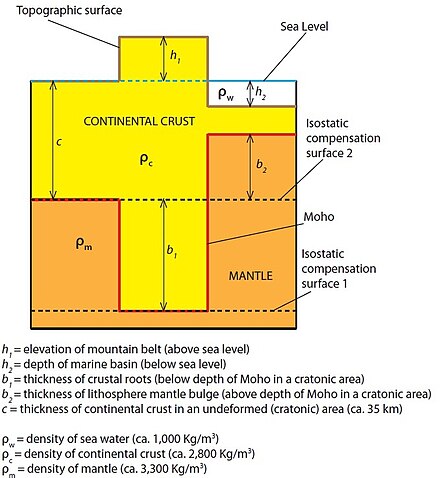
La base del modelo es la ley de Pascal , y particularmente su consecuencia de que, dentro de un fluido en equilibrio estático, la presión hidrostática es la misma en cada punto a la misma elevación (superficie de compensación hidrostática): ^{[3] [8]}

h1⋅ρ1 ​​= _h2⋅ρ2 = h3⋅ρ3 ₌ ... _hn⋅ρn​​_​​​​_​​

Para la imagen simplificada que se muestra, la profundidad de las raíces del cinturón montañoso (b ₁ ) se calcula de la siguiente manera:

${\displaystyle (h_{1}+c+b_{1})\rho _{c}=(c\rho _{c})+(b_{1}\rho _{m})}$

${\displaystyle {b_{1}(\rho _{m}-\rho _{c})}=h_{1}\rho _{c}}$

${\displaystyle b_{1}={\frac {h_{1}\rho _{c}}{\rho _{m}-\rho _{c}}}}$

donde es la densidad del manto (aprox. 3300 kg m ⁻³ ) y es la densidad de la corteza (aprox. 2750 kg m ⁻³ ). Por lo tanto, en general: ${\displaystyle \rho _{m}}$ ${\displaystyle \rho _{c}}$

b1 ≅ _5⋅ h1_​

En el caso de una topografía negativa (una cuenca marina), el equilibrio de las columnas litosféricas da:

${\displaystyle c\rho _{c}=(h_{2}\rho _{w})+(b_{2}\rho _{m})+[(c-h_{2}-b_{2})\rho _{c}]}$

${\displaystyle {b_{2}(\rho _{m}-\rho _{c})}={h_{2}(\rho _{c}-\rho _{w})}}$

${\displaystyle b_{2}=({\frac {\rho _{c}-\rho _{w}}{\rho _{m}-\rho _{c}}}){h_{2}}}$

donde es la densidad del manto (aprox. 3.300 kg m ⁻³ ), es la densidad de la corteza (aprox. 2.750 kg m ⁻³ ) y es la densidad del agua (aprox. 1.000 kg m ⁻³ ). Por lo tanto, en general: ${\displaystyle \rho _{m}}$ ${\displaystyle \rho _{c}}$ ${\displaystyle \rho _{w}}$

b2 ≅ _3,2⋅ h2_​

Pratt

Para el modelo simplificado mostrado, la nueva densidad viene dada por: , donde es la altura de la montaña y c el espesor de la corteza. ^{[3] [15]} ${\displaystyle \rho _{1}=\rho _{c}{\frac {c}{h_{1}+c}}}$ ${\displaystyle h_{1}}$

Vening Meinesz / flexión

Dibujo que muestra los movimientos verticales isostáticos de la litosfera (gris) en respuesta a una carga vertical (en verde)

Esta hipótesis se propuso para explicar cómo las grandes cargas topográficas, como las de los montes submarinos (por ejemplo, las islas hawaianas ), podrían compensarse mediante un desplazamiento regional en lugar de local de la litosfera. Esta es la solución más general para la flexión litosférica , ya que se aproxima a los modelos compensados ​​localmente anteriores a medida que la carga se vuelve mucho mayor que una longitud de onda de flexión o la rigidez flexural de la litosfera se acerca a cero. ^{[3] [9]}

Por ejemplo, el desplazamiento vertical z de una región de la corteza oceánica se describiría mediante la ecuación diferencial

${\displaystyle D{\frac {d^{4}z}{dx^{4}}}+(\rho _{m}-\rho _{w})zg=P(x)}$

donde y son las densidades de la estenosfera y del agua del océano, g es la aceleración debida a la gravedad y es la carga sobre la corteza oceánica. El parámetro D es la rigidez a la flexión , definida como ${\displaystyle \rho _{m}}$ ${\displaystyle \rho _{w}}$ ${\displaystyle P(x)}$

${\displaystyle D=ET_{c}^{3}/12(1-\sigma ^{2})}$

donde E es el módulo de Young , es el coeficiente de Poisson y es el espesor de la litosfera. Las soluciones de esta ecuación tienen un número de onda característico ${\displaystyle \sigma }$ ${\displaystyle T_{c}}$

${\displaystyle \kappa ={\sqrt[{4}]{(\rho _{m}-\rho _{w})g/4D}}}$

A medida que la capa rígida se debilita, se acerca al infinito y el comportamiento se aproxima al equilibrio hidrostático puro de la hipótesis de Airy-Heiskanen. ^[14] ${\displaystyle \kappa }$

Profundidad de compensación

La profundidad de compensación (también conocida como nivel de compensación , profundidad de compensación o nivel de compensación ) es la profundidad por debajo de la cual la presión es idéntica en cualquier superficie horizontal. En regiones estables, se encuentra en la corteza profunda, pero en regiones activas, puede estar por debajo de la base de la litosfera. ^[16] En el modelo de Pratt, es la profundidad por debajo de la cual todas las rocas tienen la misma densidad; por encima de esta profundidad, la densidad es menor donde la elevación topográfica es mayor. ^[17]

Trascendencia

Deposición y erosión

Cuando se depositan grandes cantidades de sedimentos en una región determinada, el inmenso peso de los nuevos sedimentos puede hacer que la corteza que se encuentra debajo se hunda. De manera similar, cuando se erosionan grandes cantidades de material de una región, el terreno puede elevarse para compensar. Por lo tanto, cuando se erosiona una cadena montañosa, la cadena (reducida) rebota hacia arriba (hasta cierto punto) para erosionarse aún más. Algunos de los estratos rocosos que ahora son visibles en la superficie del suelo pueden haber pasado gran parte de su historia a grandes profundidades debajo de la superficie enterrados bajo otros estratos, para finalmente quedar expuestos cuando esos otros estratos se erosionaron y las capas inferiores rebotaron hacia arriba. ^[18]

Se puede hacer una analogía con un iceberg , que siempre flota con una cierta proporción de su masa por debajo de la superficie del agua. Si cae nieve sobre la parte superior del iceberg, este se hundirá más en el agua. Si una capa de hielo se derrite en la parte superior del iceberg, el iceberg restante se elevará. De manera similar, la litosfera de la Tierra "flota" en la astenosfera. ^{[8] [19]}

Colisiones continentales

Cuando los continentes chocan, la corteza continental puede engrosarse en sus bordes en la colisión. También es muy común que una de las placas se empuje hacia abajo debajo de la otra placa. El resultado es que la corteza en la zona de colisión llega a tener un espesor de hasta 80 kilómetros (50 millas), ^[20] frente a los 40 kilómetros (25 millas) de la corteza continental promedio. ^[21] Como se señaló anteriormente, la hipótesis de Airy predice que las raíces de las montañas resultantes serán aproximadamente cinco veces más profundas que la altura de las montañas, o 32 km frente a 8 km. En otras palabras, la mayor parte de la corteza engrosada se mueve hacia abajo en lugar de hacia arriba, al igual que la mayor parte de un iceberg está debajo de la superficie del agua.

Sin embargo, los márgenes de las placas convergentes son tectónicamente muy activos y sus características superficiales están parcialmente soportadas por tensiones horizontales dinámicas, de modo que no están en completo equilibrio isostático. Estas regiones muestran las anomalías isostáticas más altas en la superficie de la Tierra. ^[22]

Dorsales medio-oceánicas

La hipótesis de Pratt explica las dorsales oceánicas como regiones superpuestas de densidad inusualmente baja en el manto superior. ^[22] Esto refleja la expansión térmica debido a las temperaturas más altas presentes bajo las dorsales. ^[23]

Cuenca y Cordillera

En la provincia de cuencas y cordilleras del oeste de América del Norte, la anomalía isostática es pequeña, excepto cerca de la costa del Pacífico, lo que indica que la región está generalmente cerca del equilibrio isostático. Sin embargo, la profundidad hasta la base de la corteza no se correlaciona fuertemente con la altura del terreno. Esto proporciona evidencia (a través de la hipótesis de Pratt) de que el manto superior en esta región no es homogéneo, con variaciones laterales significativas en la densidad. ^[22]

Capas de hielo

La formación de capas de hielo puede provocar el hundimiento de la superficie terrestre. Por el contrario, se observa un rebote isostático postglacial en áreas que alguna vez estuvieron cubiertas por capas de hielo que ahora se han derretido, como alrededor del mar Báltico ^[24] y la bahía de Hudson ^[25] . A medida que el hielo se retira, la carga sobre la litosfera y la astenosfera se reduce y estas rebotan hacia sus niveles de equilibrio. De esta manera, es posible encontrar antiguos acantilados marinos y plataformas de corte de olas asociadas a cientos de metros sobre el nivel del mar actual . Los movimientos de rebote son tan lentos que el levantamiento causado por el final del último período glacial aún continúa ^{[18] .}

Además del movimiento vertical de la tierra y el mar, el ajuste isostático de la Tierra también implica movimientos horizontales. ^[26] Puede causar cambios en el campo gravitacional de la Tierra ^[27] y la velocidad de rotación , desplazamiento polar ^[28] y terremotos . ^[29]

Límite entre litosfera y astenosfera

La hipótesis de isostasia se utiliza a menudo para determinar la posición del límite entre la litosfera y la astenosfera (LAB). ^[30]

Véase también

• Principio de Arquímedes  – Principio de flotabilidad en dinámica de fluidos
• William Bowie (ingeniero)  – Ingeniero geodésico estadounidense
• Lau, Gotland  – Distrito de la isla de Gotland, Suecia
• Terraza marina  : forma de relieve costero emergente
• Anomalía de la gravedad  : diferencia entre la aceleración gravitacional ideal y la observada en un lugar
• Mapa de gravedad
• Cronología del desarrollo de la tectonofísica (antes de 1954)

Referencias

1. 33.Spasojevic, S., y Gurnis, M., 2012, Nivel del mar y movimiento vertical de los continentes a partir de modelos dinámicos de la Tierra desde el Cretácico Superior: Boletín de la Asociación Estadounidense de Geólogos del Petróleo, v. 96, n.º 11, pág. 2037–2064.
2. 13. Foulger, GR, Pritchard, MJ, Julian, BR, Evans, JR, Allen, RM, Nolet, G., Morgan, WJ, Bergsson, BH, Erlendsson, P., Jakobsdottir, S., Ragnarsson, S., Stefansson, R., Vogfjord, K., 2000. La anomalía sísmica debajo de Islandia se extiende hasta la zona de transición del manto y no más allá. Geophys. J. Int. 142, F1–F5.
3. Watts, AB (2001). Isostasia y flexión de la litosfera . Cambridge University Press. ISBN 0521622727.
4. Dutton, Clarence (1882). "Física de la corteza terrestre; discusión". American Journal of Science . 3. 23 (abril): 283–290. Bibcode :1882AmJS...23..283D. doi :10.2475/ajs.s3-23.136.283. S2CID  128904689.
5. Orme, Antony (2007). "Clarence Edward Dutton (1841–1912): soldado, erudito y esteta". Geological Society, Londres, Special Publications . 287 (1): 271–286. Bibcode :2007GSLSP.287..271O. doi :10.1144/SP287.21. S2CID  128576633.
6. Longwell, Chester R. (1958). "Clarence Edward Dutton" (PDF) . Washington DC: Academia Nacional de Ciencias . Consultado el 24 de marzo de 2022 .
7. Kearey, P.; Klepeis, KA; Vid, FJ (2009). Tectónica global (3ª ed.). Oxford: Wiley-Blackwell. pag. 42.ISBN​ 9781405107778.
8. Kearey, Klepeis y Vine 2009, pág. 43.
9. Kearey, Klepeis y Vine 2009, págs.
10. Gilber, GK (1890). "Lago Bonneville". Monografía del Servicio Geológico de Estados Unidos . 1 . doi :10.3133/m1.
11. Kearey, Klepeis y Vine 2009, págs. 42–45.
12. Kearey, Klepeis y Vine 2009, págs. 45–48.
13. Czechowski, L. (2019). "Flujo del manto y determinación de la posición de LAB asumiendo isostasia". Geofísica pura y aplicada . 176 (6): 2451–2463. Código Bibliográfico :2019PApGe.176.2451C. doi : 10.1007/s00024-019-02093-8 .
14. Kearey, Klepeis y Vine 2009, pág. 45.
15. Kearey, Klepeis y Vine 2009, págs. 43–44.
16. Jackson, Julia A., ed. (1997). "Profundidad de compensación". Glosario de geología (cuarta edición). Alexandria, Virginia: American Geological Institute. ISBN 0922152349.
17. Allaby, Michael (2013). "Modelo Pratt". Diccionario de geología y ciencias de la tierra (cuarta edición). Oxford: Oxford University Press. ISBN 9780199653065.
18. Kearey, Klepeis y Vine 2009, págs.
19. Monroe, James S. (1992). Geología física: exploración de la Tierra . St. Paul: West Pub. Co. pág. 305. ISBN 0314921958.
20. Kearey, Klepeis y Vine 2009, pág. 322.
21. Kearey, Klepeis y Vine 2009, pág. 19.
22. Kearey, Klepeis y Vine 2009, pág. 48.
23. Philpotts, Anthony R.; Ague, Jay J. (2009). Principios de petrología ígnea y metamórfica (2.ª ed.). Cambridge, Reino Unido: Cambridge University Press. pp. 6–10. ISBN 9780521880060.
24. Eronen, Matti; Gluckert, Gunnar; Hatakka, Lassi; Van de Plassche, Orson; Van der Plicht, Johannes; Rantala, Pasi (28 de junio de 2008). "Tasas de elevación isostática del Holoceno y descenso relativo del nivel del mar en el Báltico en el suroeste de Finlandia basadas en estudios de contactos de aislamiento". Bóreas . 30 (1): 17–30. doi :10.1111/j.1502-3885.2001.tb00985.x. S2CID  54582233 . Consultado el 15 de noviembre de 2022 .
25. Balestra, Barbara; Bertini, Adele; De Vernal, Anne; Monechi, Simonetta; Reale, Viviana (1 de octubre de 2013). «Condiciones superficiales del mar en el Cuaternario Tardío en el Abanico Laurentiano: Evidencias de conjuntos de cocolitos y dinocistos». Paleogeografía, Paleoclimatología, Paleoecología . 387 : 200–210. Bibcode :2013PPP...387..200B. doi :10.1016/j.palaeo.2013.07.002 . Consultado el 15 de noviembre de 2022 .
26. James, Thomas S.; Morgan, W. Jason (junio de 1990). "Movimientos horizontales debidos al rebote postglacial". Geophysical Research Letters . 17 (7): 957–960. Código Bibliográfico :1990GeoRL..17..957J. doi :10.1029/GL017i007p00957.
27. Alexander, JC (noviembre de 1983). "Efectos armónicos superiores del campo gravitatorio de la Tierra a partir del rebote postglacial observado por Lageos". Geophysical Research Letters . 10 (11): 1085–1087. Código Bibliográfico :1983GeoRL..10.1085A. doi :10.1029/GL010i011p01085.
28. Wahr, John ; Dazhong, Han; Trupin, Andrew; Lindqvist, Varna (noviembre de 1993). "Cambios seculares en la rotación y la gravedad: ¿evidencia de un rebote postglacial o de cambios en el hielo polar?". Advances in Space Research . 13 (11): 257–269. Bibcode :1993AdSpR..13k.257W. doi :10.1016/0273-1177(93)90228-4.
29. Davenport, Colin A.; Ringrose, Philip S.; Becker, Amfried; Hancock, Paul; Fenton, Clark (1989). "Investigaciones geológicas de la actividad sísmica tardía y posglacial en Escocia". Terremotos en los márgenes pasivos del Atlántico Norte: neotectónica y rebote posglacial . págs. 175–194. doi :10.1007/978-94-009-2311-9_11. ISBN 978-94-010-7538-1.
30. Grinč, M.; Zeyen, H.; Bielik, M. (2014). "Modelado geofísico integrado 1D automático de discontinuidades litosféricas: un estudio de caso de la región de la cuenca de los Cárpatos y Panonia". Contribuciones a la geofísica y la geodesia . 44 (2): 115–131. Bibcode :2014CoGG...44..115G. doi : 10.2478/congeo-2014-0007 . S2CID  129497623 . Consultado el 13 de diciembre de 2021 .

Lectura adicional

• Lisitzin, Eugenie (1974). Cambios en el nivel del mar. Ámsterdam: Elsevier Scientific Pub. Co. ISBN 9780080870441. Recuperado el 23 de marzo de 2022 .

Enlaces externos

• Oldham, Richard Dixon (1922). "Isostasia"  . Encyclopædia Britannica (12.ª ed.).