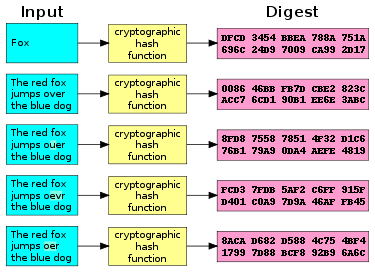
Una función hash criptográfica ( CHF ) es un algoritmo hash (un mapa de una cadena binaria arbitraria a una cadena binaria con un tamaño fijo de bits) que tiene propiedades especiales deseables para una aplicación criptográfica : [1]
Las funciones hash criptográficas tienen muchas aplicaciones en el ámbito de la seguridad de la información , en particular en firmas digitales , códigos de autenticación de mensajes (MAC) y otras formas de autenticación . También se pueden utilizar como funciones hash ordinarias , para indexar datos en tablas hash , para la toma de huellas digitales , para detectar datos duplicados o identificar archivos de forma única y como sumas de comprobación para detectar la corrupción accidental de datos. De hecho, en contextos de seguridad de la información, los valores hash criptográficos a veces se denominan huellas digitales ( digitales ) , sumas de comprobación o simplemente valores hash , aunque todos estos términos representan funciones más generales con propiedades y propósitos bastante diferentes. [2]
Las funciones hash no criptográficas se utilizan en tablas hash y para detectar errores accidentales; sus construcciones no suelen ofrecer resistencia a un ataque deliberado. Por ejemplo, un ataque de denegación de servicio en tablas hash es posible si las colisiones son fáciles de encontrar, como en el caso de las funciones de verificación de redundancia cíclica (CRC) lineales. [3]
La mayoría de las funciones hash criptográficas están diseñadas para tomar una cadena de cualquier longitud como entrada y producir un valor hash de longitud fija.
Una función hash criptográfica debe ser capaz de soportar todos los tipos conocidos de ataques criptoanalíticos . En criptografía teórica, el nivel de seguridad de una función hash criptográfica se ha definido utilizando las siguientes propiedades:
La resistencia a colisiones implica una segunda resistencia a la preimagen, pero no implica una resistencia a la preimagen. [5] La suposición más débil siempre se prefiere en criptografía teórica, pero en la práctica, una función hash que solo sea resistente a la segunda preimagen se considera insegura y, por lo tanto, no se recomienda para aplicaciones reales.
De manera informal, estas propiedades significan que un adversario malintencionado no puede reemplazar o modificar los datos de entrada sin cambiar su resumen. Por lo tanto, si dos cadenas tienen el mismo resumen, uno puede estar muy seguro de que son idénticas. La segunda resistencia a la preimagen evita que un atacante cree un documento con el mismo hash que un documento que el atacante no puede controlar. La resistencia a la colisión evita que un atacante cree dos documentos distintos con el mismo hash.
Una función que cumpla con estos criterios puede tener propiedades indeseables. Actualmente, las funciones hash criptográficas populares son vulnerables a ataques de extensión de longitud : dados hash( m ) y len( m ) pero no m , al elegir un m ′ adecuado un atacante puede calcular hash( m ∥ m ′ ) , donde ∥ denota concatenación . [6] Esta propiedad se puede utilizar para romper esquemas de autenticación ingenuos basados en funciones hash. La construcción HMAC soluciona estos problemas.
En la práctica, la resistencia a las colisiones es insuficiente para muchos usos prácticos. Además de la resistencia a las colisiones, debería ser imposible para un adversario encontrar dos mensajes con resúmenes sustancialmente similares; o inferir cualquier información útil sobre los datos, dado solo su resumen. En particular, una función hash debería comportarse tanto como sea posible como una función aleatoria (a menudo llamada oráculo aleatorio en pruebas de seguridad) y al mismo tiempo ser determinista y eficientemente computable. Esto descarta funciones como la función SWIFFT , que puede demostrarse rigurosamente como resistente a las colisiones suponiendo que ciertos problemas en redes ideales son computacionalmente difíciles, pero, como función lineal, no satisface estas propiedades adicionales. [7]
Los algoritmos de suma de comprobación, como CRC32 y otras comprobaciones de redundancia cíclica , están diseñados para cumplir con requisitos mucho más débiles y, por lo general, no son adecuados como funciones hash criptográficas. Por ejemplo, se utilizó un CRC para la integridad de los mensajes en el estándar de cifrado WEP , pero se descubrió rápidamente un ataque que explotaba la linealidad de la suma de comprobación.
En la práctica criptográfica, "difícil" generalmente significa "casi con certeza fuera del alcance de cualquier adversario al que se le debe impedir que rompa el sistema mientras la seguridad del sistema se considere importante". Por lo tanto, el significado del término depende en cierta medida de la aplicación, ya que el esfuerzo que un agente malintencionado puede poner en la tarea suele ser proporcional a la ganancia esperada. Sin embargo, dado que el esfuerzo necesario suele multiplicarse por la longitud del resumen, incluso una ventaja de mil veces en potencia de procesamiento se puede neutralizar añadiendo una docena de bits a este último.
En el caso de mensajes seleccionados de un conjunto limitado de mensajes, por ejemplo, contraseñas u otros mensajes breves, puede ser posible invertir un hash probando todos los mensajes posibles del conjunto. Debido a que las funciones hash criptográficas suelen estar diseñadas para calcularse rápidamente, se han desarrollado funciones de derivación de claves especiales que requieren mayores recursos informáticos y que dificultan estos ataques de fuerza bruta .
En algunos análisis teóricos, "difícil" tiene un significado matemático específico, como "no resoluble en tiempo polinómico asintótico ". Estas interpretaciones de la dificultad son importantes en el estudio de funciones hash criptográficas demostrablemente seguras , pero no suelen tener una fuerte conexión con la seguridad práctica. Por ejemplo, un algoritmo de tiempo exponencial a veces puede ser lo suficientemente rápido como para realizar un ataque factible. Por el contrario, un algoritmo de tiempo polinómico (por ejemplo, uno que requiere n 20 pasos para claves de n dígitos) puede ser demasiado lento para cualquier uso práctico.
Un ejemplo del uso potencial de un hash criptográfico es el siguiente: Alice le plantea a Bob un problema matemático difícil y afirma que lo ha resuelto. Bob quiere intentarlo él mismo, pero quiere estar seguro de que Alice no está mintiendo. Por lo tanto, Alice escribe su solución, calcula su hash y le dice a Bob el valor del hash (mientras mantiene la solución en secreto). Luego, cuando Bob encuentra la solución por sí mismo unos días después, Alice puede demostrar que tenía la solución antes revelándola y haciendo que Bob la copie y verifique que coincide con el valor del hash que se le dio antes. (Este es un ejemplo de un esquema de compromiso simple ; en la práctica real, Alice y Bob a menudo serán programas de computadora, y el secreto sería algo menos fácil de falsificar que una supuesta solución de un rompecabezas).
Una aplicación importante de los hashes seguros es la verificación de la integridad de los mensajes . La comparación de los resúmenes de mensajes (resúmenes de hash del mensaje) calculados antes y después de la transmisión puede determinar si se han realizado cambios en el mensaje o en el archivo .
Los resúmenes de hash MD5 , SHA-1 o SHA-2 a veces se publican en sitios web o foros para permitir la verificación de la integridad de los archivos descargados, [8] incluidos los archivos recuperados mediante el uso compartido de archivos , como la duplicación . Esta práctica establece una cadena de confianza siempre que los hashes se publiquen en un sitio confiable (normalmente el sitio de origen) autenticado por HTTPS . El uso de un hash criptográfico y una cadena de confianza detecta cambios maliciosos en el archivo. Los códigos de detección de errores no criptográficos, como las comprobaciones de redundancia cíclica, solo previenen alteraciones no maliciosas del archivo, ya que se puede crear fácilmente una falsificación intencional para que tenga el valor del código en colisión .
Casi todos los esquemas de firma digital requieren que se calcule un hash criptográfico sobre el mensaje. Esto permite que el cálculo de la firma se realice sobre un resumen de hash relativamente pequeño y de tamaño estático. El mensaje se considera auténtico si la verificación de la firma tiene éxito dada la firma y el resumen de hash recalculado sobre el mensaje. Por lo tanto, la propiedad de integridad del mensaje del hash criptográfico se utiliza para crear esquemas de firma digital seguros y eficientes.
La verificación de contraseñas generalmente se basa en hashes criptográficos. Almacenar todas las contraseñas de los usuarios como texto sin formato puede provocar una violación de seguridad masiva si el archivo de contraseñas se ve comprometido. Una forma de reducir este peligro es almacenar únicamente el resumen en hash de cada contraseña. Para autenticar a un usuario, se realiza un hash de la contraseña presentada por el usuario y se compara con el hash almacenado. Se requiere un método de restablecimiento de contraseña cuando se realiza el hash de la contraseña; las contraseñas originales no se pueden volver a calcular a partir del valor de hash almacenado.
Sin embargo, el uso de funciones hash criptográficas estándar, como la serie SHA, ya no se considera seguro para el almacenamiento de contraseñas. [9] : 5.1.1.2 Estos algoritmos están diseñados para ser calculados rápidamente, por lo que si los valores hash se ven comprometidos, es posible intentar adivinar contraseñas a altas velocidades. Las unidades de procesamiento de gráficos comunes pueden probar miles de millones de contraseñas posibles por segundo. Las funciones hash de contraseñas que realizan estiramiento de claves , como PBKDF2 , scrypt o Argon2 , comúnmente usan invocaciones repetidas de un hash criptográfico para aumentar el tiempo (y en algunos casos la memoria de la computadora) requerido para realizar ataques de fuerza bruta en los resúmenes de hash de contraseñas almacenadas. Para obtener más detalles, consulte § Ataques a contraseñas hash.
Un hash de contraseña también requiere el uso de un valor de sal aleatorio grande y no secreto que se puede almacenar con el hash de contraseña. El valor de sal se combina con la contraseña, lo que altera la asignación de hash de contraseña para cada contraseña, lo que hace que sea imposible para un adversario almacenar tablas de valores de hash precalculados con los que se pueda comparar el resumen del hash de contraseña o probar una gran cantidad de valores de hash robados en paralelo.
Un sistema (o protocolo, o función) de prueba de trabajo es una medida económica para disuadir ataques de denegación de servicio y otros abusos de servicio como el spam en una red al requerir algo de trabajo del solicitante del servicio, generalmente significa tiempo de procesamiento por parte de una computadora. Una característica clave de estos esquemas es su asimetría: el trabajo debe ser moderadamente duro (pero factible) del lado del solicitante pero fácil de verificar para el proveedor de servicios. Un sistema popular, utilizado en la minería de Bitcoin y Hashcash , utiliza inversiones de hash parciales para demostrar que se realizó el trabajo, para desbloquear una recompensa de minería en Bitcoin y como una muestra de buena voluntad para enviar un correo electrónico en Hashcash. El remitente debe encontrar un mensaje cuyo valor hash comience con un número de bits cero. El trabajo promedio que el remitente necesita realizar para encontrar un mensaje válido es exponencial en el número de bits cero requeridos en el valor hash, mientras que el destinatario puede verificar la validez del mensaje ejecutando una sola función hash. Por ejemplo, en Hashcash, se le pide al remitente que genere un encabezado cuyo valor hash SHA-1 de 160 bits tenga los primeros 20 bits como ceros. El remitente, en promedio, tendrá que intentarlo 2 19 veces para encontrar un encabezado válido.
Un resumen de mensaje también puede servir como un medio para identificar de manera confiable un archivo; varios sistemas de administración de código fuente , incluidos Git , Mercurial y Monotone , utilizan la suma de valores de varios tipos de contenido (contenido de archivos, árboles de directorios, información de ascendencia, etc.) para identificarlos de manera única. Los hashes se utilizan para identificar archivos en redes de intercambio de archivos entre pares . Por ejemplo, en un enlace ed2k , un hash de variante MD4 se combina con el tamaño del archivo, lo que proporciona información suficiente para localizar las fuentes de los archivos, descargar el archivo y verificar su contenido. Los enlaces magnet son otro ejemplo. Dichos hashes de archivos suelen ser el hash superior de una lista de hashes o un árbol de hashes , lo que permite beneficios adicionales.
Una de las principales aplicaciones de una función hash es permitir la búsqueda rápida de datos en una tabla hash . Al ser funciones hash de un tipo particular, las funciones hash criptográficas también se prestan bien a esta aplicación.
Sin embargo, en comparación con las funciones hash estándar, las funciones hash criptográficas tienden a ser mucho más costosas computacionalmente. Por esta razón, tienden a usarse en contextos donde es necesario que los usuarios se protejan contra la posibilidad de falsificación (la creación de datos con el mismo resumen que los datos esperados) por parte de participantes potencialmente maliciosos. [ cita requerida ]
El almacenamiento direccionable por contenido (CAS), también conocido como almacenamiento direccionable por contenido o almacenamiento de contenido fijo, es una forma de almacenar información para que pueda recuperarse en función de su contenido, no de su nombre o ubicación. Se ha utilizado para el almacenamiento y la recuperación a alta velocidad de contenido fijo, como documentos almacenados para cumplir con las regulaciones gubernamentales [ cita requerida ] . El almacenamiento direccionable por contenido es similar a la memoria direccionable por contenido .
Los sistemas CAS funcionan pasando el contenido del archivo a través de una función hash criptográfica para generar una clave única, la "dirección de contenido". El directorio del sistema de archivos almacena estas direcciones y un puntero al almacenamiento físico del contenido. Debido a que un intento de almacenar el mismo archivo generará la misma clave, los sistemas CAS garantizan que los archivos que contienen sean únicos y, dado que cambiar el archivo dará como resultado una nueva clave, los sistemas CAS brindan la seguridad de que el archivo no se modifica.
El CAS se convirtió en un mercado importante durante la década de 2000, especialmente después de la introducción de la Ley Sarbanes-Oxley de 2002 en los Estados Unidos, que requería el almacenamiento de enormes cantidades de documentos durante largos períodos y que solo se recuperaban en raras ocasiones. El rendimiento cada vez mayor de los sistemas de archivos tradicionales y los nuevos sistemas de software han erosionado el valor de los sistemas CAS heredados, que se han vuelto cada vez más raros después de aproximadamente 2018 [ cita requerida ] . Sin embargo, los principios de direccionabilidad de contenido continúan siendo de gran interés para los científicos informáticos y forman el núcleo de numerosas tecnologías emergentes, como el intercambio de archivos entre pares , las criptomonedas y la computación distribuida .Existen varios métodos para utilizar un cifrado de bloques para construir una función hash criptográfica, específicamente una función de compresión unidireccional .
Los métodos se parecen a los modos de operación de cifrado de bloques que se usan habitualmente para el cifrado. Muchas funciones hash conocidas, incluidas MD4 , MD5 , SHA-1 y SHA-2 , se construyen a partir de componentes similares a los de cifrado de bloques diseñados para ese fin, con retroalimentación para garantizar que la función resultante no sea invertible. Los finalistas de SHA-3 incluyeron funciones con componentes similares a los de cifrado de bloques (por ejemplo, Skein , BLAKE ), aunque la función finalmente seleccionada, Keccak , se construyó sobre una esponja criptográfica .
Se puede utilizar un cifrado de bloque estándar como AES en lugar de estos cifrados de bloque personalizados; esto puede resultar útil cuando un sistema integrado necesita implementar tanto cifrado como hash con un tamaño de código o área de hardware mínimos. Sin embargo, ese enfoque puede tener costos en eficiencia y seguridad. Los cifrados en funciones hash están diseñados para hash: utilizan claves y bloques grandes, pueden cambiar de clave de manera eficiente en cada bloque y han sido diseñados y examinados para resistir ataques de clave relacionada . Los cifrados de propósito general tienden a tener diferentes objetivos de diseño. En particular, AES tiene tamaños de clave y bloque que hacen que no sea trivial usarlo para generar valores hash largos; el cifrado AES se vuelve menos eficiente cuando la clave cambia en cada bloque; y los ataques de clave relacionada lo hacen potencialmente menos seguro para usar en una función hash que para el cifrado.
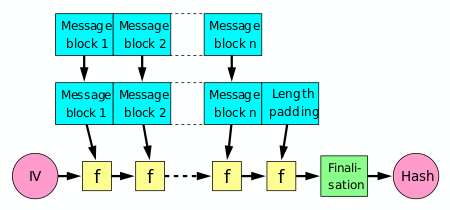
Una función hash debe ser capaz de procesar un mensaje de longitud arbitraria y convertirlo en una salida de longitud fija. Esto se puede lograr dividiendo la entrada en una serie de bloques de igual tamaño y operando sobre ellos en secuencia utilizando una función de compresión unidireccional . La función de compresión puede estar especialmente diseñada para el hash o puede construirse a partir de un cifrado de bloques. Una función hash construida con la construcción Merkle–Damgård es tan resistente a las colisiones como su función de compresión; cualquier colisión de la función hash completa puede atribuirse a una colisión en la función de compresión.
El último bloque procesado también debe tener una longitud rellenada de forma inequívoca ; esto es crucial para la seguridad de esta construcción. Esta construcción se denomina construcción Merkle–Damgård . La mayoría de las funciones hash clásicas comunes, incluidas SHA-1 y MD5 , adoptan esta forma.
Una aplicación sencilla de la construcción Merkle–Damgård, donde el tamaño de la salida hash es igual al tamaño del estado interno (entre cada paso de compresión), da como resultado un diseño hash de tubería estrecha . Este diseño causa muchos defectos inherentes, incluyendo extensión de longitud , colisiones múltiples, [10] ataques de mensajes largos, [11] ataques de generar y pegar, [ cita requerida ] y también no se puede paralelizar. Como resultado, las funciones hash modernas se construyen sobre construcciones de tubería ancha que tienen un tamaño de estado interno mayor, que van desde ajustes de la construcción Merkle–Damgård [10] hasta nuevas construcciones como la construcción de esponja y la construcción HAIFA . [12] Ninguno de los participantes en el concurso de funciones hash del NIST utiliza una construcción Merkle–Damgård clásica. [13]
Mientras tanto, truncar la salida de un hash más largo, como el utilizado en SHA-512/256, también derrota muchos de estos ataques. [14]
Las funciones hash se pueden utilizar para crear otras primitivas criptográficas . Para que estas otras primitivas sean criptográficamente seguras, se debe tener cuidado de crearlas correctamente.
Los códigos de autenticación de mensajes (MAC) (también llamados funciones hash con clave) suelen construirse a partir de funciones hash. HMAC es un MAC de este tipo.
Así como los cifrados en bloque se pueden utilizar para construir funciones hash, las funciones hash se pueden utilizar para construir cifrados en bloque. Las construcciones Luby-Rackoff que utilizan funciones hash pueden ser demostrablemente seguras si la función hash subyacente es segura. Además, muchas funciones hash (incluidas SHA-1 y SHA-2 ) se construyen utilizando un cifrado en bloque de propósito especial en una construcción Davies–Meyer u otra. Ese cifrado también se puede utilizar en un modo de operación convencional, sin las mismas garantías de seguridad; por ejemplo, SHACAL , BEAR y LION .
Los generadores de números pseudoaleatorios (PRNG) se pueden crear utilizando funciones hash. Esto se hace combinando una semilla aleatoria (secreta) con un contador y aplicando un algoritmo hash.
Algunas funciones hash, como Skein , Keccak y RadioGatún , generan un flujo de datos arbitrariamente largo y pueden usarse como un cifrado de flujo , y los cifrados de flujo también pueden construirse a partir de funciones hash de resumen de longitud fija. A menudo, esto se hace primero construyendo un generador de números pseudoaleatorios criptográficamente seguro y luego usando su flujo de bytes aleatorios como flujo de claves . SEAL es un cifrado de flujo que usa SHA-1 para generar tablas internas, que luego se usan en un generador de flujo de claves más o menos no relacionado con el algoritmo hash. No se garantiza que SEAL sea tan fuerte (o débil) como SHA-1. De manera similar, la expansión de claves de los cifrados de flujo HC-128 y HC-256 hace un uso intensivo de la función hash SHA-256 .
La concatenación de salidas de múltiples funciones hash proporciona una resistencia a las colisiones tan buena como el más fuerte de los algoritmos incluidos en el resultado concatenado. [ cita requerida ] Por ejemplo, las versiones anteriores de Transport Layer Security (TLS) y Secure Sockets Layer (SSL) usaban sumas MD5 y SHA-1 concatenadas . [15] [16] Esto garantiza que un método para encontrar colisiones en una de las funciones hash no anule los datos protegidos por ambas funciones hash. [ cita requerida ]
Para las funciones hash de construcción Merkle–Damgård , la función concatenada es tan resistente a colisiones como su componente más fuerte, pero no más resistente a colisiones. [ cita requerida ] Antoine Joux observó que las 2-colisiones conducen a n -colisiones: si es factible para un atacante encontrar dos mensajes con el mismo hash MD5, entonces puede encontrar tantos mensajes adicionales con ese mismo hash MD5 como desee, sin mayor dificultad. [17] Entre esos n mensajes con el mismo hash MD5, es probable que haya una colisión en SHA-1. El trabajo adicional necesario para encontrar la colisión SHA-1 (más allá de la búsqueda exponencial de cumpleaños) requiere solo tiempo polinomial . [18] [19]
Existen muchos algoritmos de hash criptográficos; en esta sección se enumeran algunos algoritmos a los que se hace referencia con relativa frecuencia. Se puede encontrar una lista más extensa en la página que contiene una comparación de funciones de hash criptográficas .
MD5 fue diseñado por Ronald Rivest en 1991 para reemplazar una función hash anterior, MD4, y se especificó en 1992 como RFC 1321. Las colisiones con MD5 se pueden calcular en segundos, lo que hace que el algoritmo no sea adecuado para la mayoría de los casos de uso donde se requiere un hash criptográfico. MD5 produce un resumen de 128 bits (16 bytes).
SHA-1 fue desarrollado como parte del proyecto Capstone del gobierno de los EE. UU . La especificación original, ahora comúnmente llamada SHA-0, del algoritmo fue publicada en 1993 bajo el título Secure Hash Standard, FIPS PUB 180, por la agencia de estándares del gobierno estadounidense NIST (Instituto Nacional de Estándares y Tecnología). Fue retirada por la NSA poco después de su publicación y reemplazada por la versión revisada, publicada en 1995 en FIPS PUB 180-1 y comúnmente designada SHA-1. Se pueden producir colisiones contra el algoritmo SHA-1 completo utilizando el ataque shattered y la función hash debe considerarse rota. SHA-1 produce un resumen de hash de 160 bits (20 bytes).
Los documentos pueden referirse a SHA-1 simplemente como "SHA", aunque esto pueda entrar en conflicto con otros algoritmos hash seguros como SHA-0, SHA-2 y SHA-3.
RIPEMD (RACE Integrity Primitives Evaluation Message Digest) es una familia de funciones hash criptográficas desarrolladas en Lovaina, Bélgica, por Hans Dobbertin, Antoon Bosselaers y Bart Preneel en el grupo de investigación COSIC de la Katholieke Universiteit Leuven, y publicadas por primera vez en 1996. RIPEMD se basó en los principios de diseño utilizados en MD4 y su rendimiento es similar al del más popular SHA-1. Sin embargo, RIPEMD-160 no ha sido descifrado. Como su nombre lo indica, RIPEMD-160 produce un resumen hash de 160 bits (20 bytes).
Whirlpool es una función hash criptográfica diseñada por Vincent Rijmen y Paulo SLM Barreto, quienes la describieron por primera vez en 2000. Whirlpool se basa en una versión sustancialmente modificada del Estándar de cifrado avanzado (AES). Whirlpool produce un resumen hash de 512 bits (64 bytes).
SHA-2 (Secure Hash Algorithm 2) es un conjunto de funciones hash criptográficas diseñadas por la Agencia de Seguridad Nacional de los Estados Unidos (NSA), publicadas por primera vez en 2001. Se construyen utilizando la estructura Merkle–Damgård, a partir de una función de compresión unidireccional construida a su vez utilizando la estructura Davies–Meyer a partir de un cifrado de bloque especializado (clasificado).
SHA-2 consta básicamente de dos algoritmos hash: SHA-256 y SHA-512. SHA-224 es una variante de SHA-256 con diferentes valores iniciales y salida truncada. SHA-384 y los menos conocidos SHA-512/224 y SHA-512/256 son variantes de SHA-512. SHA-512 es más seguro que SHA-256 y, por lo general, es más rápido que SHA-256 en máquinas de 64 bits como AMD64 .
El tamaño de salida en bits viene dado por la extensión del nombre "SHA", por lo que SHA-224 tiene un tamaño de salida de 224 bits (28 bytes); SHA-256, 32 bytes; SHA-384, 48 bytes; y SHA-512, 64 bytes.
El 5 de agosto de 2015, el NIST publicó SHA-3 (Secure Hash Algorithm 3). SHA-3 es un subconjunto de la familia de primitivas criptográficas más amplias, Keccak. El algoritmo Keccak es obra de Guido Bertoni, Joan Daemen, Michael Peeters y Gilles Van Assche. Keccak se basa en una construcción de esponja, que también se puede utilizar para crear otras primitivas criptográficas, como un cifrado de flujo. SHA-3 proporciona los mismos tamaños de salida que SHA-2: 224, 256, 384 y 512 bits.
También se pueden obtener tamaños de salida configurables utilizando las funciones SHAKE-128 y SHAKE-256. En este caso, las extensiones -128 y -256 del nombre implican la solidez de la seguridad de la función, en lugar del tamaño de salida en bits.
BLAKE2, una versión mejorada de BLAKE, fue anunciada el 21 de diciembre de 2012. Fue creada por Jean-Philippe Aumasson, Samuel Neves, Zooko Wilcox-O'Hearn y Christian Winnerlein con el objetivo de reemplazar los algoritmos MD5 y SHA-1, ampliamente utilizados pero defectuosos. Cuando se ejecuta en arquitecturas ARM y x64 de 64 bits, BLAKE2b es más rápido que SHA-3, SHA-2, SHA-1 y MD5. Aunque BLAKE y BLAKE2 no se han estandarizado como SHA-3, BLAKE2 se ha utilizado en muchos protocolos, incluido el hash de contraseña Argon2 , por la alta eficiencia que ofrece en las CPU modernas. Como BLAKE era un candidato para SHA-3, BLAKE y BLAKE2 ofrecen los mismos tamaños de salida que SHA-3, incluido un tamaño de salida configurable.
BLAKE3, una versión mejorada de BLAKE2, se anunció el 9 de enero de 2020. Fue creado por Jack O'Connor, Jean-Philippe Aumasson, Samuel Neves y Zooko Wilcox-O'Hearn. BLAKE3 es un algoritmo único, a diferencia de BLAKE y BLAKE2, que son familias de algoritmos con múltiples variantes. La función de compresión de BLAKE3 se basa estrechamente en la de BLAKE2, con la mayor diferencia siendo que el número de rondas se reduce de 10 a 7. Internamente, BLAKE3 es un árbol de Merkle y admite mayores grados de paralelismo que BLAKE2.
Existe una larga lista de funciones hash criptográficas, pero se ha descubierto que muchas son vulnerables y no deberían utilizarse. Por ejemplo, el NIST seleccionó 51 funciones hash [20] como candidatas para la primera ronda de la competición de hash SHA-3, de las cuales 10 se consideraron rotas y 16 mostraron debilidades significativas y, por lo tanto, no pasaron a la siguiente ronda; se puede encontrar más información en el artículo principal sobre las competiciones de funciones hash del NIST .
Incluso si una función hash nunca ha sido violada, un ataque exitoso contra una variante debilitada puede socavar la confianza de los expertos. Por ejemplo, en agosto de 2004 se encontraron colisiones en varias funciones hash que eran populares en ese momento, incluida MD5. [21] Estas debilidades pusieron en tela de juicio la seguridad de los algoritmos más fuertes derivados de las funciones hash débiles, en particular, SHA-1 (una versión reforzada de SHA-0), RIPEMD-128 y RIPEMD-160 (ambas versiones reforzadas de RIPEMD). [22]
El 12 de agosto de 2004, Joux, Carribault, Lemuel y Jalby anunciaron una colisión para el algoritmo SHA-0 completo. [17] Joux et al. lograron esto utilizando una generalización del ataque de Chabaud y Joux. Encontraron que la colisión tenía una complejidad de 2,51 y requería aproximadamente 80.000 horas de CPU en una supercomputadora con 256 procesadores Itanium 2 , lo que equivale a 13 días de uso a tiempo completo de la supercomputadora. [ cita requerida ]
En febrero de 2005, se informó de un ataque a SHA-1 que encontraría colisiones en aproximadamente 2 69 operaciones de hash, en lugar de las 2 80 esperadas para una función hash de 160 bits. En agosto de 2005, se informó de otro ataque a SHA-1 que encontraría colisiones en 2 63 operaciones. Se han conocido otras debilidades teóricas de SHA-1, [23] [24] y en febrero de 2017 Google anunció una colisión en SHA-1. [25] Los investigadores de seguridad recomiendan que las nuevas aplicaciones puedan evitar estos problemas utilizando miembros posteriores de la familia SHA, como SHA-2 , o utilizando técnicas como el hash aleatorio [26] que no requieren resistencia a colisiones.
Un ataque práctico y exitoso rompió el MD5 (usado en los certificados para la seguridad de la capa de transporte ) en 2008. [27]
Muchos algoritmos hash criptográficos se basan en la construcción Merkle–Damgård . Todos los algoritmos hash criptográficos que utilizan directamente la salida completa de una construcción Merkle–Damgård son vulnerables a ataques de extensión de longitud . Esto hace que los algoritmos hash MD5, SHA-1, RIPEMD-160, Whirlpool y SHA-256/SHA-512 sean vulnerables a este ataque específico. SHA-3, BLAKE2, BLAKE3 y las variantes truncadas de SHA-2 no son vulnerables a este tipo de ataque. [ cita requerida ]
En lugar de almacenar contraseñas de usuario simples, los sistemas de acceso controlado con frecuencia almacenan el hash de la contraseña de cada usuario en un archivo o base de datos. Cuando alguien solicita acceso, la contraseña que envía se codifica y se compara con el valor almacenado. Si la base de datos es robada (algo que ocurre con demasiada frecuencia [28] ), el ladrón solo tendrá los valores hash, no las contraseñas.
Un atacante aún puede recuperar contraseñas a partir de los hashes, porque la mayoría de las personas eligen contraseñas de manera predecible. Las listas de contraseñas comunes circulan ampliamente y muchas contraseñas son lo suficientemente cortas como para que se puedan probar incluso todas las combinaciones posibles si el cálculo del hash no lleva demasiado tiempo. [29]
El uso de sal criptográfica previene algunos ataques, como la creación de archivos de valores hash precomputados, por ejemplo, tablas arcoiris . Pero las búsquedas del orden de 100 mil millones de pruebas por segundo son posibles con procesadores gráficos de alta gama , lo que hace posibles los ataques directos incluso con sal. [30] [31] El Instituto Nacional de Estándares y Tecnología de los Estados Unidos recomienda almacenar contraseñas utilizando hashes especiales llamados funciones de derivación de claves (KDF) que se han creado para ralentizar las búsquedas de fuerza bruta. [9] : 5.1.1.2 Los hashes lentos incluyen pbkdf2 , bcrypt , scrypt , argon2 , Balloon y algunos modos recientes de Unix crypt . Para las KDF que realizan múltiples hashes para ralentizar la ejecución, el NIST recomienda un recuento de iteraciones de 10 000 o más. [9] : 5.1.1.2
más que los algoritmos de cifrado, las funciones hash unidireccionales son los caballos de batalla de la criptografía moderna.