Regla de subdivisión finita

Manera de dividir el polígono en partes más pequeñas.

Una proyección en perspectiva de una teselación dodecaédrica en H 3 . Tenga en cuenta la estructura recursiva: cada pentágono contiene pentágonos más pequeños, que contienen pentágonos más pequeños. Este es un ejemplo de una regla de subdivisión que surge de un universo finito (es decir, una variedad cerrada de 3 ).

En matemáticas, una regla de subdivisión finita es una forma recursiva de dividir un polígono u otra forma bidimensional en partes cada vez más pequeñas. Las reglas de subdivisión en cierto sentido son generalizaciones de fractales geométricos regulares . En lugar de repetir exactamente el mismo diseño una y otra vez, tienen ligeras variaciones en cada etapa, lo que permite una estructura más rica manteniendo el estilo elegante de los fractales. ^[1] Las reglas de subdivisión se han utilizado en arquitectura, biología e informática, así como en el estudio de variedades hiperbólicas . Los mosaicos de sustitución son un tipo de regla de subdivisión bien estudiado.

Definición

Una regla de subdivisión toma un mosaico del plano por polígonos y lo convierte en un nuevo mosaico subdividiendo cada polígono en polígonos más pequeños. Es finito si hay un número finito de formas en las que cada polígono puede subdividirse. Cada forma de subdividir un mosaico se denomina tipo de mosaico . Cada tipo de mosaico está representado por una etiqueta (normalmente una letra). Cada tipo de mosaico se subdivide en tipos de mosaico más pequeños. Cada borde también se subdivide según un número finito de tipos de bordes . Las reglas de subdivisión finita solo pueden subdividir mosaicos formados por polígonos etiquetados por tipos de mosaico. Estos mosaicos se denominan complejos de subdivisión para la regla de subdivisión. Dado cualquier complejo de subdivisión para una regla de subdivisión, podemos subdividirlo una y otra vez para obtener una secuencia de teselaciones.

Por ejemplo, la subdivisión binaria tiene un tipo de mosaico y un tipo de borde:

La regla de la subdivisión binaria

Dado que el único tipo de mosaico es un cuadrilátero, la subdivisión binaria solo puede subdividir mosaicos formados por cuadriláteros. Esto significa que los únicos complejos de subdivisión son los mosaicos por cuadriláteros. El mosaico puede ser regular , pero no tiene por qué serlo:

Empezamos con un complejo de cuatro cuadriláteros y lo subdividimos dos veces. Todos los cuadrados son fichas tipo A.

Aquí comenzamos con un complejo formado por cuatro cuadriláteros y lo subdividimos dos veces. Todos los cuadriláteros son fichas tipo A.

Ejemplos de reglas de subdivisión finitas

La subdivisión baricéntrica es un ejemplo de una regla de subdivisión con un tipo de arista (que se subdivide en dos aristas) y un tipo de mosaico (un triángulo que se subdivide en 6 triángulos más pequeños). Cualquier superficie triangulada es un complejo de subdivisión baricéntrica. ^[1]

El mosaico de Penrose se puede generar mediante una regla de subdivisión en un conjunto de cuatro tipos de mosaicos (las líneas curvas en la siguiente tabla solo ayudan a mostrar cómo encajan los mosaicos):

Ciertos mapas racionales dan lugar a reglas de subdivisión finitas. ^[2] Esto incluye la mayoría de los mapas de Lattès . ^[3]

Cada nudo alterno o complemento de enlace primo, no dividido, tiene una regla de subdivisión, con algunas fichas que no se subdividen, correspondientes al límite del complemento de enlace. ^[4] Las reglas de subdivisión muestran cómo se vería el cielo nocturno para alguien que viviera en un complemento de nudos ; Debido a que el universo se envuelve alrededor de sí mismo (es decir, no está simplemente conectado ), un observador vería que el universo visible se repite en un patrón infinito. La regla de subdivisión describe ese patrón.

La regla de subdivisión se ve diferente para diferentes geometrías. Ésta es una regla de subdivisión para el nudo trébol , que no es un nudo hiperbólico :

Regla de subdivisión del trébol

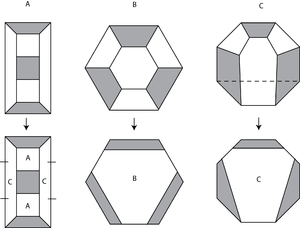
Y esta es la regla de subdivisión de los anillos borromeos , que es hiperbólica:

Regla de subdivisión borromea

En cada caso, la regla de subdivisión actuaría sobre algún mosaico de una esfera (es decir, el cielo nocturno), pero es más fácil dibujar simplemente una pequeña parte del cielo nocturno, correspondiente a un solo mosaico que se subdivide repetidamente. Esto es lo que sucede con el nudo trébol:

Subdivisiones del complejo de subdivisiones para el complemento trébol.

Y para los anillos borromeos:

Se complementan las subdivisiones del complejo de subdivisiones de los anillos borromeos.

Reglas de subdivisión en dimensiones superiores.

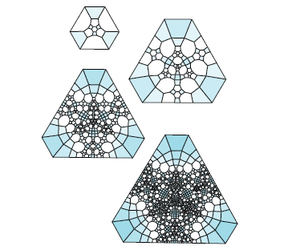
Las reglas de subdivisión se pueden generalizar fácilmente a otras dimensiones. ^[5] Por ejemplo, la subdivisión baricéntrica se utiliza en todas las dimensiones. Además, la subdivisión binaria se puede generalizar a otras dimensiones (donde los hipercubos se dividen por cada plano medio), como en la prueba del teorema de Heine-Borel .

Definición rigurosa

Una regla de subdivisión para los cuatro toros. Las caras de las fichas B que se subdividen solo pueden tocar las fichas C, y las caras de las fichas B que no solo tocan las fichas A.

Una regla de subdivisión finita consta de lo siguiente. ^[1] ${\displaystyle R}$

1. Un complejo CW bidimensional finito , llamado complejo de subdivisión , con una estructura de celdas fija tal que es la unión de sus 2 celdas cerradas. Suponemos que para cada 2 celdas cerradas de hay una estructura CW en un disco 2 cerrado tal que tiene al menos dos vértices, los vértices y los bordes de están contenidos en , y el mapa característico que se asigna a se restringe a un homeomorfismo en cada celda abierta. ${\displaystyle S_{R}}$ ${\displaystyle S_{R}}$ ${\displaystyle {\tilde {s}}}$ ${\displaystyle S_{R}}$ ${\displaystyle s}$ ${\displaystyle s}$ ${\displaystyle s}$ ${\displaystyle \partial s}$ ${\displaystyle \psi _{s}:s\rightarrow S_{R}}$ ${\displaystyle {\tilde {s}}}$

2. Un complejo CW bidimensional finito , que es una subdivisión de . ${\displaystyle R(S_{R})}$ ${\displaystyle S_{R}}$

3.Un mapa celular continuo llamado mapa de subdivisión , cuya restricción a cada celda abierta es un homeomorfismo sobre una celda abierta. ${\displaystyle \phi _{R}:R(S_{R})\rightarrow S_{R}}$

Cada complejo CW en la definición anterior (con su mapa característico dado ) se denomina tipo mosaico . ${\displaystyle s}$ ${\displaystyle \psi _{s}}$

Un complejo - para una regla de subdivisión es un complejo CW bidimensional que es la unión de sus 2 celdas cerradas, junto con un mapa celular continuo cuya restricción a cada celda abierta es un homeomorfismo. Podemos subdividirlo en un complejo exigiendo que el mapa inducido se restrinja a un homeomorfismo en cada celda abierta. es nuevamente un complejo con map . Repitiendo este proceso, obtenemos una secuencia de complejos subdivididos con mapas . ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle X}$ ${\displaystyle f:X\rightarrow S_{R}}$ ${\displaystyle X}$ ${\displaystyle R(X)}$ ${\displaystyle f:R(X)\rightarrow R(S_{R})}$ ${\displaystyle R(X)}$ ${\displaystyle R}$ ${\displaystyle \phi _{R}\circ f:R(X)\rightarrow S_{R}}$ ${\displaystyle R}$ ${\displaystyle R^{n}(X)}$ ${\displaystyle \phi _{R}^{n}\circ f:R^{n}(X)\rightarrow S_{R}}$

La subdivisión binaria es un ejemplo: ^[6]

La regla de la subdivisión binaria.

El complejo de subdivisión se puede crear pegando los bordes opuestos del cuadrado, haciendo que el complejo de subdivisión forme un toroide . El mapa de subdivisión es el mapa de duplicación en el toroide, envolviendo el meridiano alrededor de sí mismo dos veces y la longitud alrededor de sí mismo dos veces. Este es un mapa de cobertura cuádruple . El plano, mosaico de cuadrados, es un complejo de subdivisión para esta regla de subdivisión, con el mapa de estructura dado por el mapa de cobertura estándar. En la subdivisión, cada cuadrado del plano se subdivide en cuadrados de un cuarto del tamaño. ${\displaystyle S_{R}}$ ${\displaystyle \phi }$ ${\displaystyle f:\mathbb {R} ^{2}\rightarrow R(S_{R})}$

Propiedades de cuasiisometría

El gráfico histórico de la regla de subdivisión de los tercios medios .

Las reglas de subdivisión se pueden utilizar para estudiar las propiedades cuasiisométricas de ciertos espacios. ^[7] Dadas una regla de subdivisión y un complejo de subdivisión , podemos construir un gráfico llamado gráfico histórico que registra la acción de la regla de subdivisión. El gráfico consta de los gráficos duales de cada etapa , junto con los bordes que conectan cada mosaico con sus subdivisiones . ${\displaystyle R}$ ${\displaystyle X}$ ${\displaystyle R^{n}(X)}$ ${\displaystyle R^{n}(X)}$ ${\displaystyle R^{n+1}(X)}$

Las propiedades de cuasiisometría del gráfico histórico se pueden estudiar utilizando reglas de subdivisión. Por ejemplo, el gráfico histórico es cuasi isométrico al espacio hiperbólico exactamente cuando la regla de subdivisión es conforme , como se describe en el teorema combinatorio de mapeo de Riemann . ^[7]

Aplicaciones

Aplicaciones de las reglas de subdivisión.

Los mosaicos islámicos de Girih en la arquitectura islámica son mosaicos autosimilares que se pueden modelar con reglas de subdivisión finitas. ^[8] En 2007, Peter J. Lu de la Universidad de Harvard y el profesor Paul J. Steinhardt de la Universidad de Princeton publicaron un artículo en la revista Science sugiriendo que los mosaicos girih poseían propiedades consistentes con mosaicos cuasicristalinos fractales autosemejantes como los mosaicos de Penrose (presentación de 1974). , obras predecesoras que comenzaron aproximadamente en 1964) las antecedieron en cinco siglos. ^[8]

Las superficies de subdivisión en gráficos por computadora utilizan reglas de subdivisión para refinar una superficie a cualquier nivel de precisión determinado. Estas superficies de subdivisión (como la superficie de subdivisión de Catmull-Clark ) toman una malla poligonal (del tipo que se usa en las películas animadas en 3D) y la refinan hasta obtener una malla con más polígonos agregando y desplazando puntos según diferentes fórmulas recursivas. ^[9] Aunque muchos puntos se desplazan en este proceso, cada nueva malla es combinatoriamente una subdivisión de la malla anterior (lo que significa que para cada borde y vértice de la malla anterior, puede identificar un borde y un vértice correspondientes en la nueva, más varias aristas y vértices más).

Cannon, Floyd y Parry (2000) aplicaron reglas de subdivisión al estudio de patrones de crecimiento a gran escala de organismos biológicos. ^[6] Cannon, Floyd y Parry produjeron un modelo de crecimiento matemático que demostró que algunos sistemas determinados por reglas de subdivisión finitas simples pueden dar como resultado objetos (en su ejemplo, el tronco de un árbol) cuya forma a gran escala oscila violentamente con el tiempo, a pesar de que la Las leyes de subdivisión locales siguen siendo las mismas. ^[6] Cannon, Floyd y Parry también aplicaron su modelo al análisis de los patrones de crecimiento del tejido de rata. ^[6] Sugirieron que la naturaleza "curvada negativamente" (o no euclidiana) de los patrones de crecimiento microscópicos de los organismos biológicos es una de las razones clave por las que los organismos a gran escala no parecen cristales o formas poliédricas, sino que, de hecho, en muchos casos se parecen a fractales autosemejantes . ^[6] En particular, sugirieron que dicha estructura local "curvada negativamente" se manifiesta en la naturaleza altamente plegada y altamente conectada del cerebro y el tejido pulmonar. ^[6]

La conjetura de Cannon.

Cannon , Floyd y Parry estudiaron por primera vez reglas de subdivisión finitas como un intento de probar la siguiente conjetura:

Conjetura de Cannon : cada grupo hiperbólico de Gromov con una 2 esferas en el infinito actúa geométricamente en un espacio 3 hiperbólico . ^[7]

Aquí, una acción geométrica es una acción cocompacta, propiamente discontinua, por isometrías. Esta conjetura fue resuelta parcialmente por Grigori Perelman en su prueba ^{[10] [11] [12]} de la conjetura de geometrización , que establece (en parte) que cualquier grupo hiperbólico de Gromov que sea un grupo de 3 variedades debe actuar geométricamente sobre 3-variedades hiperbólicas. espacio. Sin embargo, aún queda por demostrar que un grupo hiperbólico de Gromov con dos esferas en el infinito es un grupo de tres variedades.

Cannon y Swenson demostraron ^[13] que un grupo hiperbólico con dos esferas en el infinito tiene una regla de subdivisión asociada. Si esta regla de subdivisión es conforme en cierto sentido, el grupo será un grupo de 3 variedades con la geometría del 3-espacio hiperbólico. ^[7]

Teorema de mapeo combinatorio de Riemann

Las reglas de subdivisión dan una secuencia de mosaicos de una superficie, y los mosaicos dan una idea de distancia, longitud y área (al permitir que cada mosaico tenga longitud y área 1). En el límite, las distancias que provienen de estos mosaicos pueden converger en algún sentido a una estructura analítica en la superficie. El teorema combinatorio de mapeo de Riemann proporciona las condiciones necesarias y suficientes para que esto ocurra. ^[7]

Su declaración necesita algunos antecedentes. Un mosaico de un anillo (es decir, un anillo cerrado) da dos invariantes, y , llamados módulos aproximados . Estos son similares al módulo clásico de un anillo . Se definen mediante el uso de funciones de peso . Una función de peso asigna un número no negativo llamado peso a cada mosaico de . A cada camino se le puede asignar una longitud, definida como la suma de los pesos de todos los mosaicos en el camino. Defina la altura de debajo como el mínimo de la longitud de todos los caminos posibles que conectan el límite interior con el límite exterior. La circunferencia de under es el mínimo de la longitud de todos los caminos posibles que rodean el anillo (es decir, no es nulohomotópico en R). El área de under se define como la suma de los cuadrados de todos los pesos en . Luego define ${\displaystyle T}$ ${\displaystyle R}$ ${\displaystyle M_{\sup }(R,T)}$ ${\displaystyle m_{\inf }(R,T)}$ ${\displaystyle \rho }$ ${\displaystyle T}$ ${\displaystyle R}$ ${\displaystyle H(\rho )}$ ${\displaystyle R}$ ${\displaystyle \rho }$ ${\displaystyle R}$ ${\displaystyle C(\rho )}$ ${\displaystyle R}$ ${\displaystyle \rho }$ ${\displaystyle A(\rho )}$ ${\displaystyle R}$ ${\displaystyle \rho }$ ${\displaystyle R}$

${\displaystyle M_{\sup }(R,T)=\sup {\frac {H(\rho )^{2}}{A(\rho )}},}$

${\displaystyle m_{\inf }(R,T)=\inf {\frac {A(\rho )}{C(\rho )^{2}}}.}$

Tenga en cuenta que son invariantes bajo la escala de la métrica.

Una secuencia de teselados es conforme ( ) si la malla se aproxima a 0 y: ${\displaystyle T_{1},T_{2},\ldots }$ ${\displaystyle K}$

1. Para cada anillo , los módulos aproximados y , para todos los suficientemente grandes, se encuentran en un único intervalo de la forma ; y ${\displaystyle R}$ ${\displaystyle M_{\sup }(R,T_{i})}$ ${\displaystyle m_{\inf }(R,T_{i})}$ ${\displaystyle i}$ ${\displaystyle [r,Kr]}$
2. Dado un punto en la superficie, una vecindad de y un número entero , hay un anillo que separa x del complemento de , de modo que para todos los grandes los módulos aproximados de son todos mayores que . ^[7] ${\displaystyle x}$ ${\displaystyle N}$ ${\displaystyle x}$ ${\displaystyle I}$ ${\displaystyle R}$ ${\displaystyle N\smallsetminus \{x\}}$ ${\displaystyle N}$ ${\displaystyle i}$ ${\displaystyle R}$ ${\displaystyle I}$

Declaración del teorema

Si una secuencia de mosaicos de una superficie es conforme ( ) en el sentido anterior, entonces hay una estructura conforme en la superficie y una constante que depende únicamente de en qué módulos clásicos y módulos aproximados (de para suficientemente grande) de cualquier anillo dado son comparables, lo que significa que se encuentran en un solo intervalo . ^[7] ${\displaystyle T_{1},T_{2},\ldots }$ ${\displaystyle K}$ ${\displaystyle K'}$ ${\displaystyle K}$ ${\displaystyle T_{i}}$ ${\displaystyle i}$ ${\displaystyle K'}$ ${\displaystyle [r,K'r]}$

Consecuencias

El teorema combinatorio de mapeo de Riemann implica que un grupo actúa geométricamente si y solo si es hiperbólico de Gromov, tiene una esfera en el infinito y la regla de subdivisión natural de la esfera da lugar a una secuencia de teselaciones que es conforme en el sentido anterior. . Por tanto, la conjetura de Cannon sería cierta si todas esas reglas de subdivisión fueran conformes. ^[13] ${\displaystyle G}$ ${\displaystyle \mathbb {H} ^{3}}$

Referencias

1. C JW Cannon, WJ Floyd, WR Parry. Reglas de subdivisión finitas . Geometría y dinámica conformes, vol. 5 (2001), págs. 153-196.
2. JW Cannon, WJ Floyd, WR Parry. Construir reglas de subdivisión a partir de mapas racionales . Geometría y dinámica conformes, vol. 11 (2007), págs. 128-136.
3. JW Cannon, WJ Floyd, WR Parry. Mapas de Lattès y reglas de subdivisión . Geometría y dinámica conformes, vol. 14 (2010, págs. 113-140.
4. B. Rushton. Construir reglas de subdivisión a partir de enlaces alternos . Ajustarse. Geom. Din. 14 (2010), 1-13.
5. Rushton, B. (2012). "Una regla de subdivisión finita para el toroide n-dimensional". Geometriae Dedicata . 167 : 23–34. arXiv : 1110.3310 . doi :10.1007/s10711-012-9802-5. S2CID  119145306.
6. JW Cannon, W. Floyd y W. Parry. Crecimiento de cristales, crecimiento de células biológicas y geometría. Formación de patrones en biología, visión y dinámica, págs. 65–82. Científico mundial, 2000. ISBN 981-02-3792-8 , ISBN 978-981-02-3792-9 .  
7. James W. Cannon. El teorema combinatorio de mapeo de Riemann. Acta Mathematica 173 (1994), núm. 2, págs. 155-234.
8. Lu, Peter J.; Steinhardt, Paul J. (2007). "Azulejos decagonales y cuasicristalinos en la arquitectura islámica medieval" (PDF) . Ciencia . 315 (5815): 1106–1110. Código Bib : 2007 Ciencia... 315.1106L. doi : 10.1126/ciencia.1135491. PMID  17322056. S2CID  10374218. Archivado desde el original (PDF) el 7 de octubre de 2009.
   "Material de apoyo en línea" (PDF) . Archivado desde el original (PDF) el 26 de marzo de 2009.
9. D. Zorin. Subdivisiones sobre mallas arbitrarias: algoritmos y teoría . Serie de notas de conferencias del Instituto de Ciencias Matemáticas (Singapur). 2006.
10. Perelman, Grisha (11 de noviembre de 2002). "La fórmula de entropía para el flujo de Ricci y sus aplicaciones geométricas". arXiv : math.DG/0211159 .
11. Perelman, Grisha (10 de marzo de 2003). "Ricci fluye con cirugía en tres colectores". arXiv : math.DG/0303109 .
12. Perelman, Grisha (17 de julio de 2003). "Tiempo de extinción finito para las soluciones del flujo de Ricci en ciertas tres variedades". arXiv : math.DG/0307245 .
13. JW Cannon y EL Swenson, Reconocimiento de grupos discretos de curvatura constante en dimensión 3 . Transacciones de la Sociedad Matemática Estadounidense 350 (1998), no. 2, págs. 809–849.

enlaces externos

• Página de investigación de Bill Floyd. Esta página contiene la mayoría de los trabajos de investigación de Cannon, Floyd y Parry sobre reglas de subdivisión, así como una galería de reglas de subdivisión.