Las reglas de Pauling son cinco reglas publicadas por Linus Pauling en 1929 para predecir y racionalizar las estructuras cristalinas de los compuestos iónicos . [1] [2]
En los sólidos iónicos típicos, los cationes son más pequeños que los aniones y cada catión está rodeado de aniones coordinados que forman un poliedro . La suma de los radios iónicos determina la distancia catión-anión, mientras que la relación de radios catión-anión (o ) determina el número de coordinación (CN) del catión, así como la forma del poliedro coordinado de aniones. [2] : 524 [3]
Para los números de coordinación y los poliedros correspondientes de la tabla siguiente, Pauling derivó matemáticamente la relación mínima de radios para la cual el catión está en contacto con el número dado de aniones (considerando los iones como esferas rígidas). Si el catión es más pequeño, no estará en contacto con los aniones, lo que genera inestabilidad que conduce a un número de coordinación más bajo.

Los tres diagramas de la derecha corresponden a una coordinación octaédrica con un número de coordinación de seis: cuatro aniones en el plano de los diagramas y dos (no se muestran) por encima y por debajo de este plano. El diagrama central muestra la relación mínima de radios. El catión y dos aniones cualesquiera forman un triángulo rectángulo , con , o . Entonces . Pruebas geométricas similares arrojan las relaciones mínimas de radios para los casos altamente simétricos CN = 3, 4 y 8. [4]


Para CN = 6 y una relación de radios mayor que el mínimo, el cristal es más estable ya que el catión sigue en contacto con seis aniones, pero los aniones están más alejados entre sí, de modo que su repulsión mutua se reduce. Entonces se puede formar un octaedro con una relación de radios mayor o igual a 0,414, pero a medida que la relación aumenta por encima de 0,732, una geometría cúbica se vuelve más estable. Esto explica por qué Na + en NaCl con una relación de radios de 0,55 tiene coordinación octaédrica, mientras que Cs + en CsCl con una relación de radios de 0,93 tiene coordinación cúbica. [5]
Si la relación del radio es menor que el mínimo, dos aniones tenderán a separarse y los cuatro restantes se reorganizarán en una geometría tetraédrica donde todos estarán en contacto con el catión.
Las reglas de la relación de radios son una primera aproximación que tiene cierto éxito en la predicción de números de coordinación, pero existen muchas excepciones. [3] En un conjunto de más de 5000 óxidos , solo el 66% de los entornos de coordinación concuerdan con la primera regla de Pauling. Los óxidos formados con cationes de metales alcalinos o alcalinotérreos que contienen múltiples coordinaciones de cationes son desviaciones comunes de esta regla. [6]
Para un catión dado, Pauling definió [2] la fuerza del enlace electrostático con cada anión coordinado como , donde z es la carga del catión y ν es el número de coordinación del catión. Una estructura iónica estable se organiza para preservar la electroneutralidad local , de modo que la suma de las fuerzas de los enlaces electrostáticos con un anión sea igual a la carga de ese anión.
donde es la carga del anión y la suma es sobre los cationes adyacentes. Para sólidos simples, son iguales para todos los cationes coordinados a un anión dado, de modo que el número de coordinación del anión es la carga del anión dividida por cada fuerza de enlace electrostático. En la tabla se dan algunos ejemplos.
Pauling demostró que esta regla es útil para limitar las posibles estructuras a considerar para cristales más complejos como el mineral de aluminosilicato ortoclasa , KAlSi 3 O 8 , con tres cationes diferentes. [2] Sin embargo, a partir del análisis de datos de óxidos de la Base de datos de estructura cristalina inorgánica (ICSD), el resultado mostró que solo el 20% de todos los átomos de oxígeno coincidían con la predicción de la segunda regla (usando un punto de corte de 0,01). [6]
El hecho de que dos poliedros aniónicos compartan aristas y, en particular, caras, disminuye la estabilidad de una estructura iónica. El hecho de que compartan vértices no disminuye tanto la estabilidad, por lo que (por ejemplo) los octaedros pueden compartir vértices entre sí. [2] : 559
La disminución de la estabilidad se debe a que compartir aristas y caras coloca a los cationes más cerca unos de otros, de modo que aumenta la repulsión electrostática catión-catión. El efecto es mayor para los cationes con carga alta y CN bajo (especialmente cuando r+/r- se acerca al límite inferior de la estabilidad poliédrica). Generalmente, los elementos más pequeños cumplen mejor la regla. [6]
Como ejemplo, Pauling consideró las tres formas minerales del dióxido de titanio , cada una con un número de coordinación de 6 para los cationes Ti 4+ . La forma más estable (y más abundante) es el rutilo , en el que los octaedros de coordinación están dispuestos de modo que cada uno comparte solo dos aristas (y ninguna cara) con los octaedros adyacentes. Las otras dos formas, menos estables, son la brookita y la anatasa , en las que cada octaedro comparte tres y cuatro aristas respectivamente con los octaedros adyacentes. [2] : 559
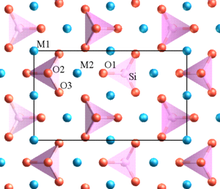
En un cristal que contiene diferentes cationes, aquellos de alta valencia y pequeño número de coordinación tienden a no compartir elementos del poliedro entre sí. [2] : 561 Esta regla tiende a aumentar la distancia entre cationes altamente cargados, a fin de reducir la repulsión electrostática entre ellos.
Uno de los ejemplos de Pauling es el olivino , M 2 SiO 4 , donde M es una mezcla de Mg 2+ en algunos sitios y Fe 2+ en otros. La estructura contiene tetraedros de SiO 4 distintos que no comparten ningún oxígeno (en las esquinas, bordes o caras) entre sí. Los cationes Mg 2+ y Fe 2+ de valencia más baja están rodeados por poliedros que sí comparten oxígeno.
La cantidad de componentes esencialmente diferentes en un cristal tiende a ser pequeña. [2] Las unidades repetidas tenderán a ser idénticas porque cada átomo de la estructura es más estable en un entorno específico. Puede haber dos o tres tipos de poliedros, como tetraedros u octaedros, pero no habrá muchos tipos diferentes.
En un estudio de 5000 óxidos, sólo el 13% de ellos satisfacen las últimas 4 reglas, lo que indica una universalidad limitada de las reglas de Pauling. [6]