Crecimiento hiperbólico

Función de crecimiento que presenta una singularidad en un tiempo finito

La función recíproca , que exhibe crecimiento hiperbólico.

Cuando una cantidad crece hacia una singularidad bajo una variación finita (una " singularidad de tiempo finito ") se dice que experimenta un crecimiento hiperbólico . ^[1] Más precisamente, la función recíproca tiene una hipérbola como gráfico, y tiene una singularidad en 0, lo que significa que el límite es infinito: se dice que cualquier gráfico similar exhibe un crecimiento hiperbólico. ${\displaystyle 1/x}$ ${\displaystyle x\to 0}$

Descripción

Si la salida de una función es inversamente proporcional a su entrada, o inversamente proporcional a la diferencia con un valor dado , la función exhibirá un crecimiento hiperbólico, con una singularidad en . ${\displaystyle x_{0}}$ ${\displaystyle x_{0}}$

En el mundo real, el crecimiento hiperbólico se crea mediante ciertos mecanismos de retroalimentación positiva no lineal . ^[2]

Comparaciones con otras funciones de crecimiento

Ecuaciones de crecimiento

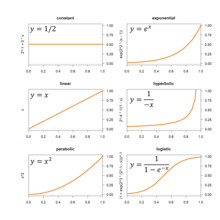
Al igual que el crecimiento exponencial y el crecimiento logístico , el crecimiento hiperbólico es altamente no lineal , pero difiere en aspectos importantes. Estas funciones pueden confundirse, ya que el crecimiento exponencial, el crecimiento hiperbólico y la primera mitad del crecimiento logístico son funciones convexas ; sin embargo, su comportamiento asintótico (comportamiento a medida que aumenta el valor de entrada) difiere drásticamente:

• El crecimiento logístico está restringido (tiene un límite finito, aun cuando el tiempo tiende al infinito),
• el crecimiento exponencial crece hasta el infinito a medida que el tiempo tiende al infinito (pero siempre es finito para un tiempo finito),
• El crecimiento hiperbólico tiene una singularidad en el tiempo finito (crece hasta el infinito en un tiempo finito).

Aplicaciones

Población

Ciertos modelos matemáticos sugieren que hasta principios de la década de 1970 la población mundial experimentó un crecimiento hiperbólico (véase, por ejemplo, Introducción a la macrodinámica social de Andrey Korotayev et al. ). También se demostró que hasta la década de 1970 el crecimiento hiperbólico de la población mundial estuvo acompañado de un crecimiento cuadrático-hiperbólico del PIB mundial , y se desarrollaron varios modelos matemáticos que describen tanto este fenómeno como la retirada del Sistema Mundial del régimen de explosión observado en las décadas recientes. Andrey Korotayev y sus colegas han correlacionado el crecimiento hiperbólico de la población mundial y el crecimiento cuadrático-hiperbólico del PIB mundial observados hasta la década de 1970 con una retroalimentación positiva no lineal de segundo orden entre el crecimiento demográfico y el desarrollo tecnológico, descrito por una cadena de causalidad: el crecimiento tecnológico conduce a una mayor capacidad de carga de la tierra para las personas, lo que conduce a más personas, lo que conduce a más inventores, lo que a su vez conduce a un crecimiento tecnológico aún mayor, y así sucesivamente. ^[3] También se ha demostrado que los modelos hiperbólicos de este tipo pueden utilizarse para describir de forma bastante precisa el crecimiento global de la complejidad planetaria de la Tierra desde 4 mil millones a. C. hasta el presente. ^[4] Otros modelos sugieren un crecimiento exponencial , un crecimiento logístico u otras funciones.

Teoría de colas

Otro ejemplo de crecimiento hiperbólico se puede encontrar en la teoría de colas : el tiempo de espera promedio de los clientes que llegan aleatoriamente crece hiperbólicamente en función de la relación de carga promedio del servidor. La singularidad en este caso ocurre cuando la cantidad promedio de trabajo que llega al servidor es igual a la capacidad de procesamiento del servidor. Si las necesidades de procesamiento exceden la capacidad del servidor, entonces no hay un tiempo de espera promedio bien definido, ya que la cola puede crecer sin límite. Una implicación práctica de este ejemplo particular es que para los sistemas de colas altamente cargados, el tiempo de espera promedio puede ser extremadamente sensible a la capacidad de procesamiento.

Cinética enzimática

Otro ejemplo práctico de crecimiento hiperbólico se puede encontrar en la cinética enzimática . Cuando se representa gráficamente la velocidad de reacción (denominada velocidad) entre una enzima y un sustrato frente a diversas concentraciones del sustrato, se obtiene un gráfico hiperbólico para muchos sistemas más simples. Cuando esto sucede, se dice que la enzima sigue la cinética de Michaelis-Menten .

Ejemplo matemático

La función

${\displaystyle x(t)={\frac {1}{t_{c}-t}}}$

exhibe un crecimiento hiperbólico con una singularidad en el tiempo : en el límite cuando , la función tiende a infinito. ${\displaystyle t_{c}}$ ${\displaystyle t\to t_{c}}$

De manera más general, la función

${\displaystyle x(t)={\frac {K}{t_{c}-t}}}$

exhibe un crecimiento hiperbólico, donde es un factor de escala . ${\displaystyle K}$

Nótese que esta función algebraica puede considerarse como una solución analítica para la diferencial de la función: ^[5]

${\displaystyle {\frac {dx}{dt}}={\frac {K}{(t_{c}-t)^{2}}}={\frac {x^{2}}{K}}}$

Esto significa que con un crecimiento hiperbólico la tasa de crecimiento absoluto de la variable x en el momento t es proporcional al cuadrado del valor de x en el momento t .

Respectivamente, la función cuadrático-hiperbólica se ve así:

${\displaystyle x(t)={\frac {K}{(t_{c}-t)^{2}}}.}$

Véase también

• Crecimiento exponencial
• Crecimiento logístico
• Singularidad matemática

Notas

1. Véase, por ejemplo, Korotayev A., Malkov A., Khaltourina D. Introducción a la macrodinámica social: macromodelos compactos del crecimiento del sistema mundial. Moscú: URSS Publishers, 2006. P. 19-20.
2. Véase, por ejemplo, Alexander V. Markov y Andrey V. Korotayev (2007). "La biodiversidad marina del fanerozoico sigue una tendencia hiperbólica". Palaeoworld. Volumen 16. Número 4. Páginas 311-318.
3. Véase, por ejemplo, Korotayev A., Malkov A., Khaltourina D. Introducción a la macrodinámica social: macromodelos compactos del crecimiento del sistema mundial. Moscú: URSS Publishers, 2006; Korotayev AV Un macromodelo compacto de la evolución del sistema mundial // Journal of World-Systems Research 11/1 (2005): 79–93. Archivado el 25 de septiembre de 2009 en Wayback Machine . Para un análisis matemático detallado de este tema, véase Un modelo matemático compacto del crecimiento económico y demográfico del sistema mundial, 1 CE - 1973 CE. "Revista internacional de modelos y métodos matemáticos en ciencias aplicadas". 2016. Vol. 10, págs. 200-209.
4. La singularidad del siglo XXI y sus implicaciones en la Gran Historia: un nuevo análisis. Journal of Big History 2/3 (2018): 71 - 118; véase también La singularidad del siglo XXI y los futuros globales. Una perspectiva desde la Gran Historia (Springer, 2020).
5. Véase, por ejemplo, Korotayev A., Malkov A., Khaltourina D. Introducción a la macrodinámica social: macromodelos compactos del crecimiento del sistema mundial. Moscú: URSS Publishers, 2006. P. 118-123.

Referencias

• Alexander V. Markov y Andrey V. Korotayev (2007). "La biodiversidad marina del fanerozoico sigue una tendencia hiperbólica". Palaeoworld . Volumen 16. Número 4. Páginas 311-318].
• Kremer, Michael . 1993. "Crecimiento de la población y cambio tecnológico: un millón antes de Cristo hasta 1990", The Quarterly Journal of Economics 108(3): 681-716.
• Korotayev A. , Malkov A., Khaltourina D. 2006. Introducción a la macrodinámica social: macromodelos compactos del crecimiento del sistema mundial. Moscú: URSS. ISBN  5-484-00414-4 .
• Rein Taagepera (1979) Personas, habilidades y recursos: Un modelo de interacción para el crecimiento de la población mundial. Pronóstico tecnológico y cambio social 13, 13-30.