El método del esfuerzo lógico , término acuñado por Ivan Sutherland y Bob Sproull en 1991, es una técnica sencilla que se utiliza para calcular el retardo en un circuito CMOS . Si se utiliza correctamente, puede ayudar a seleccionar las puertas para una función determinada (incluido el número de etapas necesarias) y a dimensionar las puertas para lograr el mínimo retardo posible para un circuito.
El retardo se expresa en términos de una unidad de retardo básica, τ = 3RC , el retardo de un inversor que acciona un inversor idéntico sin ninguna capacitancia adicional añadida por interconexiones u otras cargas; el número sin unidad asociado con esto se conoce como el retardo normalizado . (Algunos autores prefieren definir la unidad de retardo básica como el abanico de salida de 4 delay: el retardo de un inversor que acciona 4 inversores idénticos). El retardo absoluto se define entonces simplemente como el producto del retardo normalizado de la compuerta, d , y τ :
En un proceso típico de 600 nm , τ es de aproximadamente 50 ps. En un proceso de 250 nm, τ es de aproximadamente 20 ps. En los procesos modernos de 45 nm, el retraso es de aproximadamente 4 a 5 ps.
El retardo normalizado en una compuerta lógica se puede expresar como una suma de dos términos principales: el retardo parásito normalizado , p (que es un retardo intrínseco de la compuerta y se puede encontrar considerando que la compuerta no funciona con carga) y el esfuerzo de etapa , f (que depende de la carga como se describe a continuación). En consecuencia,
El esfuerzo de etapa se divide en dos componentes: un esfuerzo lógico , g , que es la relación entre la capacitancia de entrada de una compuerta dada y la de un inversor capaz de entregar la misma corriente de salida (y, por lo tanto, es una constante para una clase particular de compuerta y puede describirse como la captura de las propiedades intrínsecas de la compuerta), y un esfuerzo eléctrico , h , que es la relación entre la capacitancia de entrada de la carga y la de la compuerta. Tenga en cuenta que el "esfuerzo lógico" no tiene en cuenta la carga y, por lo tanto, tenemos el término "esfuerzo eléctrico" que tiene en cuenta la carga. El esfuerzo de etapa es entonces simplemente:
La combinación de estas ecuaciones produce una ecuación básica que modela el retraso normalizado a través de una sola puerta lógica:
Los inversores CMOS a lo largo de la ruta crítica suelen estar diseñados con una gamma igual a 2. En otras palabras, el pFET del inversor está diseñado con el doble de ancho (y, por lo tanto, el doble de capacitancia) que el nFET del inversor, para obtener aproximadamente la misma resistencia del pFET que la resistencia del nFET, para obtener aproximadamente la misma corriente de pull-up y corriente de pull-down. [1] [2]
Elija tamaños para todos los transistores de manera que el accionamiento de salida de la compuerta sea igual al accionamiento de salida de un inversor construido a partir de un PMOS de tamaño 2 y un NMOS de tamaño 1.
La excitación de salida de una puerta es igual al mínimo (sobre todas las combinaciones posibles de entradas) de la excitación de salida de la puerta para esa entrada.
El accionamiento de salida de una puerta para una entrada dada es igual al accionamiento en su nodo de salida.
El impulso en un nodo es igual a la suma de los impulsos de todos los transistores que están habilitados y cuya fuente o drenador está en contacto con el nodo en cuestión. Un transistor PMOS está habilitado cuando su voltaje de compuerta es 0. Un transistor NMOS está habilitado cuando su voltaje de compuerta es 1.
Una vez elegidos los tamaños, el esfuerzo lógico de la salida de la compuerta es la suma de los anchos de todos los transistores cuya fuente o drenador esté en contacto con el nodo de salida. El esfuerzo lógico de cada entrada a la compuerta es la suma de los anchos de todos los transistores cuya compuerta esté en contacto con ese nodo de entrada.
El esfuerzo lógico de toda la puerta es la relación entre su esfuerzo lógico de salida y la suma de sus esfuerzos lógicos de entrada.
Una ventaja importante del método de esfuerzo lógico es que se puede extender rápidamente a circuitos compuestos de múltiples etapas. El retardo de trayectoria normalizado total D se puede expresar en términos de un esfuerzo de trayectoria global , F , y el retardo parásito de trayectoria P (que es la suma de los retardos parásitos individuales):
El esfuerzo de la trayectoria se expresa en términos del esfuerzo lógico de la trayectoria G (el producto de los esfuerzos lógicos individuales de las puertas) y el esfuerzo eléctrico de la trayectoria H (la relación entre la carga de la trayectoria y su capacitancia de entrada).
Para rutas donde cada puerta acciona solo una puerta adicional (es decir, la siguiente puerta en la ruta),
Sin embargo, para los circuitos que se ramifican, se debe tener en cuenta un esfuerzo de ramificación adicional , b , que es la relación entre la capacitancia total impulsada por la compuerta y la capacitancia en el camino de interés:
Esto produce un esfuerzo de ramificación de trayectoria B que es el producto de los esfuerzos de ramificación de cada etapa; el esfuerzo de trayectoria total es entonces
Se puede observar que b = 1 para las puertas que controlan solo una puerta adicional, lo que fija B = 1 y hace que la fórmula se reduzca a la versión anterior sin ramificaciones.
Se puede demostrar que en redes lógicas multietapa, el mínimo retraso posible a lo largo de una ruta particular se puede lograr diseñando el circuito de manera que los esfuerzos de la etapa sean iguales. Para una combinación dada de puertas y una carga conocida, B , G y H son todas fijas, lo que hace que F sea fija; por lo tanto, las puertas individuales deben dimensionarse de manera que los esfuerzos de la etapa individual sean
donde N es el número de etapas del circuito.
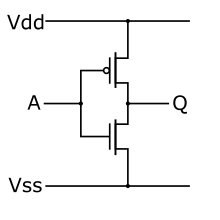
Por definición, el esfuerzo lógico g de un inversor es 1. Si el inversor acciona un inversor equivalente, el esfuerzo eléctrico h también es 1.
El retardo parásito p de un inversor también es 1 (esto se puede encontrar considerando el modelo de retardo de Elmore del inversor).
Por lo tanto, el retardo normalizado total de un inversor que acciona un inversor equivalente es
El esfuerzo lógico de una compuerta NAND de dos entradas se calcula en g = 4/3 porque una compuerta NAND con una capacidad de entrada de 4 puede impulsar la misma corriente que el inversor, con una capacidad de entrada de 3. De manera similar, el esfuerzo lógico de una compuerta NOR de dos entradas se puede encontrar en g = 5/3. Debido al menor esfuerzo lógico, las compuertas NAND suelen preferirse a las compuertas NOR.
Para puertas más grandes, el esfuerzo lógico es el siguiente:
El retardo parásito normalizado de las puertas NAND y NOR es igual al número de entradas.
Por lo tanto, el retardo normalizado de una puerta NAND de dos entradas que activa una copia idéntica de sí misma (de modo que el esfuerzo eléctrico es 1) es
y para una puerta NOR de dos entradas, el retardo es