Autómata finito determinista

Máquina de estados finitos

Un ejemplo de un autómata finito determinista que acepta únicamente números binarios que son múltiplos de 3. El estado S ₀ es tanto el estado inicial como el estado de aceptación. Por ejemplo, la cadena "1001" conduce a la secuencia de estados S ₀ , S ₁ , S ₂ , S ₁ , S ₀ y, por lo tanto, se acepta.

En la teoría de la computación , una rama de la informática teórica , un autómata finito determinista ( DFA ), también conocido como aceptor finito determinista ( DFA ), máquina de estados finitos determinista ( DFSM ) o autómata de estados finitos determinista ( DFSA ), es una máquina de estados finitos que acepta o rechaza una cadena dada de símbolos, al ejecutarse a través de una secuencia de estados determinada de forma única por la cadena. ^[1] Determinista se refiere a la unicidad de la ejecución del cálculo. En la búsqueda de los modelos más simples para capturar máquinas de estados finitos, Warren McCulloch y Walter Pitts estuvieron entre los primeros investigadores en introducir un concepto similar al de autómata finito en 1943. ^{[2] [3]}

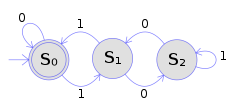
La figura ilustra un autómata finito determinista que utiliza un diagrama de estados . En este autómata de ejemplo, hay tres estados: S ₀ , S ₁ y S ₂ (indicados gráficamente por círculos). El autómata toma una secuencia finita de 0 y 1 como entrada. Para cada estado, hay una flecha de transición que conduce al siguiente estado tanto para 0 como para 1. Al leer un símbolo, un DFA salta de manera determinista de un estado a otro siguiendo la flecha de transición. Por ejemplo, si el autómata está actualmente en el estado S ₀ y el símbolo de entrada actual es 1, entonces salta de manera determinista al estado S ₁ . Un DFA tiene un estado de inicio (indicado gráficamente por una flecha que aparece de la nada) donde comienzan los cálculos, y un conjunto de estados de aceptación (indicados gráficamente por un círculo doble) que ayudan a definir cuándo un cálculo es exitoso.

Un DFA se define como un concepto matemático abstracto, pero a menudo se implementa en hardware y software para resolver diversos problemas específicos, como el análisis léxico y la comparación de patrones . Por ejemplo, un DFA puede modelar software que decide si las entradas de los usuarios en línea, como las direcciones de correo electrónico, son sintácticamente válidas o no. ^[4]

Los DFA se han generalizado a autómatas finitos no deterministas (NFA) que pueden tener varias flechas de la misma etiqueta comenzando desde un estado. Utilizando el método de construcción de conjuntos de potencias , cada NFA se puede traducir a un DFA que reconoce el mismo lenguaje. Los DFA, y también los NFA, reconocen exactamente el conjunto de lenguajes regulares . ^[1]

Definición formal

Un autómata finito determinista M es una 5- tupla , ( Q , Σ, δ , q ₀ , F ) , que consta de

• un conjunto finito de estados Q
• un conjunto finito de símbolos de entrada llamado alfabeto Σ
• una función de transición δ  : Q × Σ → Q
• un estado inicial o de inicio ${\displaystyle q_{0}\in Q}$
• un conjunto de estados de aceptación ${\displaystyle F\subseteq Q}$

Sea w = a ₁ a ₂ ... a _n una cadena sobre el alfabeto Σ . El autómata M acepta la cadena w si en Q existe una secuencia de estados, r ₀ , r ₁ , ..., r _n , con las siguientes condiciones:

1. r0 = q0_​​
2. r _{i +1} = δ ( r _i , a _{i +1} ) , para i = 0, ..., n − 1
3. ${\displaystyle r_{n}\in F}$.

En palabras, la primera condición dice que la máquina arranca en el estado inicial q ₀ . La segunda condición dice que dado cada carácter de la cadena w , la máquina pasará de un estado a otro según la función de transición δ . La última condición dice que la máquina acepta w si la última entrada de w hace que la máquina se detenga en uno de los estados de aceptación. En caso contrario, se dice que el autómata rechaza la cadena. El conjunto de cadenas que M acepta es el lenguaje reconocido por M y este lenguaje se denota por L ( M ) .

Un autómata finito determinista sin estados de aceptación y sin un estado inicial se conoce como sistema de transición o semiautómata .

Para una introducción más completa de la definición formal, consulte la teoría de autómatas .

Ejemplo

El siguiente ejemplo es de un DFA M , con un alfabeto binario, que requiere que la entrada contenga un número par de 0.

El diagrama de estados para M

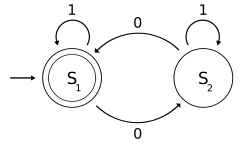
M = ( Q , Σ, δ , q ₀ , F ) donde

• Q = { S1 , S2 _}​
• Σ = {0, 1}
• q0 = S1_​​
• F = { S ₁ } y
• δ se define mediante la siguiente tabla de transición de estados :

El estado S ₁ representa que hasta ahora ha habido un número par de 0 en la entrada, mientras que S ₂ significa un número impar. Un 1 en la entrada no cambia el estado del autómata. Cuando la entrada finaliza, el estado mostrará si la entrada contenía un número par de 0 o no. Si la entrada contenía un número par de 0, M finalizará en el estado S ₁ , un estado de aceptación, por lo que se aceptará la cadena de entrada.

El lenguaje reconocido por M es el lenguaje regular dado por la expresión regular (1*) (0 (1*) 0 (1*))* , donde *es la estrella de Kleene , por ejemplo, 1*denota cualquier número (posiblemente cero) de unos consecutivos.

Variaciones

Completo e incompleto

Según la definición anterior, los autómatas finitos deterministas son siempre completos : definen a partir de cada estado una transición para cada símbolo de entrada.

Si bien esta es la definición más común, algunos autores usan el término autómata finito determinista para una noción ligeramente diferente: un autómata que define como máximo una transición para cada estado y cada símbolo de entrada; se permite que la función de transición sea parcial . ^[5] Cuando no se define ninguna transición, dicho autómata se detiene.

Autómatas locales

Un autómata local es un DFA, no necesariamente completo, para el cual todas las aristas con la misma etiqueta conducen a un único vértice. Los autómatas locales aceptan la clase de lenguajes locales , aquellos para los cuales la pertenencia de una palabra al lenguaje está determinada por una "ventana deslizante" de longitud dos en la palabra. ^{[6] [7]}

Un grafo Myhill sobre un alfabeto A es un grafo dirigido con un conjunto de vértices A y subconjuntos de vértices etiquetados como "inicio" y "fin". El lenguaje aceptado por un grafo Myhill es el conjunto de caminos dirigidos desde un vértice de inicio a un vértice de fin: el grafo actúa así como un autómata. ^[6] La clase de lenguajes aceptados por los grafos Myhill es la clase de lenguajes locales. ^[8]

Aleatoriedad

Cuando se ignoran el estado inicial y los estados de aceptación, un DFA de n estados y un alfabeto de tamaño k se puede ver como un dígrafo de n vértices en el que todos los vértices tienen k arcos de salida etiquetados 1, ..., k (un dígrafo k -out). Se sabe que cuando k ≥ 2 es un entero fijo, con alta probabilidad, el componente fuertemente conectado (SCC) más grande en un dígrafo k -out elegido uniformemente al azar es de tamaño lineal y puede ser alcanzado por todos los vértices. ^[9] También se ha demostrado que si se permite que k aumente a medida que n aumenta, entonces todo el dígrafo tiene una transición de fase para una conectividad fuerte similar al modelo de Erdős–Rényi para la conectividad. ^[10]

En un DFA aleatorio, la cantidad máxima de vértices alcanzables desde un vértice es muy cercana a la cantidad de vértices en el SCC más grande con alta probabilidad. ^{[9] [11]} Esto también es cierto para el subdígrafo inducido más grande de grado de entrada mínimo uno, que puede verse como una versión dirigida de 1 -core . ^[10]

Propiedades del cierre

El autómata superior izquierdo reconoce el idioma de todas las cadenas binarias que contienen al menos una ocurrencia de "00". El autómata inferior derecho reconoce todas las cadenas binarias con un número par de "1". El autómata inferior izquierdo se obtiene como producto de los dos anteriores, reconoce la intersección de ambos idiomas.

Si los DFA reconocen los idiomas que se obtienen al aplicar una operación sobre los idiomas reconocibles del DFA, se dice que los DFA están cerrados bajo la operación. Los DFA están cerrados bajo las siguientes operaciones.

• Unión
• Intersección ^{[12] : 59–60} (ver imagen)
• Concatenación
• Complementar
• Cierre de Kleene
• Reversión ^[13]
• Cociente ^[13]
• Sustitución ^[14]
• Homomorfismo ^{[13] [14]}

Para cada operación, se ha determinado una construcción óptima con respecto al número de estados en la investigación de la complejidad de estados . Dado que los DFA son equivalentes a los autómatas finitos no deterministas (NFA), estos cierres también pueden demostrarse utilizando propiedades de cierre de NFA.

Como un monoide de transición

Una ejecución de un DFA dado puede verse como una secuencia de composiciones de una formulación muy general de la función de transición consigo misma. Aquí construimos esa función.

Para un símbolo de entrada dado , se puede construir una función de transición definiendo para todos . (Este truco se llama currying .) Desde esta perspectiva, "actúa" sobre un estado en Q para producir otro estado. Se puede entonces considerar el resultado de la composición de funciones aplicada repetidamente a las diversas funciones , , y así sucesivamente. Dado un par de letras , se puede definir una nueva función , donde denota composición de funciones. ${\displaystyle a\in \Sigma }$ ${\displaystyle \delta _{a}:Q\rightarrow Q}$ ${\displaystyle \delta _{a}(q)=\delta (q,a)}$ ${\displaystyle q\in Q}$ ${\displaystyle \delta _{a}}$ ${\displaystyle \delta _{a}}$ ${\displaystyle \delta _{b}}$ ${\displaystyle a,b\in \Sigma }$ ${\displaystyle {\widehat {\delta }}_{ab}=\delta _{a}\circ \delta _{b}}$ ${\displaystyle \circ }$

Claramente, este proceso puede continuar de forma recursiva, obteniéndose la siguiente definición recursiva de : ${\displaystyle {\widehat {\delta }}:Q\times \Sigma ^{\star }\rightarrow Q}$

${\displaystyle {\widehat {\delta }}(q,\epsilon )=q}$, donde está la cadena vacía y ${\displaystyle \epsilon }$

${\displaystyle {\widehat {\delta }}(q,wa)=\delta _{a}({\widehat {\delta }}(q,w))}$, donde y . ${\displaystyle w\in \Sigma ^{*},a\in \Sigma }$ ${\displaystyle q\in Q}$

${\displaystyle {\widehat {\delta }}}$ se define para todas las palabras . Una ejecución del DFA es una secuencia de composiciones de con sí misma. ${\displaystyle w\in \Sigma ^{*}}$ ${\displaystyle {\widehat {\delta }}}$

La composición de funciones repetidas forma un monoide . Para las funciones de transición, este monoide se conoce como monoide de transición o, a veces, semigrupo de transformación . La construcción también se puede invertir: dado un , se puede reconstruir un , por lo que las dos descripciones son equivalentes. ${\displaystyle {\widehat {\delta }}}$ ${\displaystyle \delta }$

Ventajas y desventajas

Los DFA son uno de los modelos de computación más prácticos, ya que existe un algoritmo trivial lineal en tiempo y espacio constante en línea para simular un DFA en un flujo de entrada. Además, existen algoritmos eficientes para encontrar un DFA que reconoce:

• el complemento del lenguaje reconocido por un DFA dado.
• la unión/intersección de los idiomas reconocidos por dos DFA dados.

Dado que los DFA se pueden reducir a una forma canónica ( DFA mínimos ), también existen algoritmos eficientes para determinar:

• Si un DFA acepta cadenas (problema de vacío)
• Si un DFA acepta todas las cadenas (problema de universalidad)
• Si dos DFA reconocen el mismo idioma (problema de igualdad)
• si el idioma reconocido por un DFA está incluido en el idioma reconocido por un segundo DFA (problema de inclusión)
• El DFA con un número mínimo de estados para un lenguaje regular en particular (problema de minimización)

Los DFA son equivalentes en potencia de cálculo a los autómatas finitos no deterministas (NFA). Esto se debe, en primer lugar, a que cualquier DFA también es un NFA, por lo que un NFA puede hacer lo que un DFA puede hacer. Además, dado un NFA, utilizando la construcción de conjuntos de potencias se puede construir un DFA que reconozca el mismo lenguaje que el NFA, aunque el DFA podría tener un número exponencialmente mayor de estados que el NFA. ^{[15] [16]} Sin embargo, aunque los NFA son computacionalmente equivalentes a los DFA, los problemas mencionados anteriormente no se resuelven necesariamente de manera eficiente también para los NFA. El problema de no universalidad para los NFA es PSPACE completo ya que hay NFA pequeños con la palabra de rechazo más corta en tamaño exponencial. Un DFA es universal si y solo si todos los estados son estados finales, pero esto no se cumple para los NFA. Los problemas de igualdad, inclusión y minimización también son PSPACE completos ya que requieren formar el complemento de un NFA que da como resultado una explosión exponencial de tamaño. ^[17]

Por otra parte, los autómatas de estados finitos tienen un poder estrictamente limitado en los lenguajes que pueden reconocer; muchos lenguajes simples, incluyendo cualquier problema que requiera más que un espacio constante para resolverse, no pueden ser reconocidos por un DFA. El ejemplo clásico de un lenguaje descrito de manera simple que ningún DFA puede reconocer es el lenguaje de corchetes o Dyck , es decir, el lenguaje que consiste en corchetes correctamente emparejados como la palabra "(()())". Intuitivamente, ningún DFA puede reconocer el lenguaje Dyck porque los DFA no son capaces de contar: un autómata tipo DFA necesita tener un estado para representar cualquier número posible de paréntesis "actualmente abiertos", lo que significa que necesitaría un número ilimitado de estados. Otro ejemplo más simple es el lenguaje que consiste en cadenas de la forma a ⁿ b ⁿ para un número finito pero arbitrario de a ' s, seguido de un número igual de b ' s. ^[18]

Identificación de DFA a partir de palabras etiquetadas

Dado un conjunto de palabras positivas y un conjunto de palabras negativas , se puede construir un DFA que acepte todas las palabras de y rechace todas las palabras de : este problema se llama identificación de DFA (síntesis, aprendizaje). Si bien algunos DFA se pueden construir en tiempo lineal, el problema de identificar un DFA con el número mínimo de estados es NP-completo. ^[19] El primer algoritmo para la identificación mínima de DFA ha sido propuesto por Trakhtenbrot y Barzdin ^[20] y se llama algoritmo TB . Sin embargo, el algoritmo TB supone que todas las palabras de hasta una longitud dada están contenidas en . ${\displaystyle S^{+}\subset \Sigma ^{*}}$ ${\displaystyle S^{-}\subset \Sigma ^{*}}$ ${\displaystyle S^{+}}$ ${\displaystyle S^{-}}$ ${\displaystyle \Sigma }$ ${\displaystyle S^{+}\cup S^{-}}$

Más tarde, K. Lang propuso una extensión del algoritmo TB que no utiliza ninguna suposición sobre y , el algoritmo Traxbar . ^[21] Sin embargo, Traxbar no garantiza la minimalidad del DFA construido. En su trabajo ^[19] EM Gold también propuso un algoritmo heurístico para la identificación mínima de DFA. El algoritmo de Gold supone que y contienen un conjunto característico del lenguaje regular; de lo contrario, el DFA construido será inconsistente con o . Otros algoritmos de identificación de DFA notables incluyen el algoritmo RPNI, ^[22] el algoritmo de fusión de estados impulsado por evidencia Blue-Fringe, ^[23] y Windowed-EDSM. ^[24] Otra dirección de investigación es la aplicación de algoritmos evolutivos : el algoritmo evolutivo de etiquetado de estado inteligente ^[25] permitió resolver un problema de identificación de DFA modificado en el que los datos de entrenamiento (conjuntos y ) son ruidosos en el sentido de que algunas palabras se atribuyen a clases incorrectas. ${\displaystyle S^{+}}$ ${\displaystyle S^{-}}$ ${\displaystyle S^{+}}$ ${\displaystyle S^{-}}$ ${\displaystyle S^{+}}$ ${\displaystyle S^{-}}$ ${\displaystyle S^{+}}$ ${\displaystyle S^{-}}$

Otro paso adelante se debe a la aplicación de los solucionadores SAT por Marjin JH Heule y S. Verwer: el problema de identificación de DFA mínimo se reduce a decidir la satisfacibilidad de una fórmula booleana. ^[26] La idea principal es construir un aceptador de árbol de prefijos aumentado (un trie que contiene todas las palabras de entrada con las etiquetas correspondientes) basado en los conjuntos de entrada y reducir el problema de encontrar un DFA con estados a colorear los vértices del árbol con estados de tal manera que cuando los vértices con un color se fusionan en un estado, el autómata generado es determinista y cumple con y . Aunque este enfoque permite encontrar el DFA mínimo, sufre de una explosión exponencial del tiempo de ejecución cuando aumenta el tamaño de los datos de entrada. Por lo tanto, el algoritmo inicial de Heule y Verwer se ha ampliado posteriormente con la realización de varios pasos del algoritmo EDSM antes de la ejecución del solucionador SAT: el algoritmo DFASAT. ^[27] Esto permite reducir el espacio de búsqueda del problema, pero conduce a la pérdida de la garantía de minimidad. Ulyantsev et al. ^[28] propusieron otra forma de reducir el espacio de búsqueda mediante nuevos predicados de ruptura de simetría basados ​​en el algoritmo de búsqueda en amplitud : los estados del DFA buscado se restringen para que se numeren de acuerdo con el algoritmo BFS lanzado desde el estado inicial. Este enfoque reduce el espacio de búsqueda eliminando los autómatas isomorfos. ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle S^{+}}$ ${\displaystyle S^{-}}$ ${\displaystyle C!}$

Modelos equivalentes

Máquinas de Turing de sólo lectura y movimiento hacia la derecha

Las máquinas de Turing de solo lectura con movimiento hacia la derecha son un tipo particular de máquina de Turing que solo se mueve hacia la derecha; son casi exactamente equivalentes a los DFA. ^{[29] La definición basada en una cinta infinita simple es una} tupla de 7

${\displaystyle M=\langle Q,\Gamma ,b,\Sigma ,\delta ,q_{0},F\rangle ,}$

dónde

${\displaystyle Q}$es un conjunto finito de estados ;

${\displaystyle \Gamma }$es un conjunto finito del alfabeto/símbolos de la cinta ;

${\displaystyle b\in \Gamma }$es el símbolo en blanco (el único símbolo que puede aparecer en la cinta infinitamente a menudo en cualquier paso durante el cálculo);

${\displaystyle \Sigma }$, un subconjunto de no incluir b , es el conjunto de símbolos de entrada ; ${\displaystyle \Gamma }$

${\displaystyle \delta :Q\times \Gamma \to Q\times \Gamma \times \{R\}}$es una función llamada función de transición , R es un movimiento hacia la derecha (un desplazamiento hacia la derecha);

${\displaystyle q_{0}\in Q}$es el estado inicial ;

${\displaystyle F\subseteq Q}$es el conjunto de estados finales o de aceptación .

La máquina siempre acepta un lenguaje regular. Debe existir al menos un elemento del conjunto F (un estado HALT ) para que el lenguaje no esté vacío.

Ejemplo de una máquina de Turing de solo lectura de 3 estados y 2 símbolos

${\displaystyle Q=\{A,B,C,{\text{HALT}}\};}$

${\displaystyle \Gamma =\{0,1\};}$

${\displaystyle b=0}$, "blanco";

${\displaystyle \Sigma =\varnothing }$, conjunto vacío;

${\displaystyle \delta =}$ver tabla de estados arriba;

${\displaystyle q_{0}=A}$, estado inicial;

${\displaystyle F=}$el conjunto de un elemento de estados finales: . ${\displaystyle \{{\text{HALT}}\}}$

Véase también

• Autómata de estado finito acíclico determinista
• Minimización de DFA
• Lógica monádica de segundo orden
• Construcción de conjuntos de potencia
• Autómata cuántico finito
• Problema de separación de palabras
• Máquina de Turing
• Autómata finito de dos vías
• Autómata ponderado

Notas

1. Hopcroft 2001
2. McCulloch y Pitts (1943)
3. Rabin y Scott (1959)
4. Bai, Gina R.; Clee, Brian; Shrestha, Nischal; Chapman, Carl; Wright, Cimone; Stolee, Kathryn T. (2019). "Explorando herramientas y estrategias utilizadas durante tareas de composición de expresiones regulares". En Guéhéneuc, Yann-Gaël; Khomh, Foutse; Sarro, Federica (eds.). Actas de la 27.ª Conferencia Internacional sobre Comprensión de Programas, ICPC 2019, Montreal, QC, Canadá, 25-31 de mayo de 2019. IEEE / ACM. págs. 197–208. doi :10.1109/ICPC.2019.00039.
5. Mogensen, Torben Ægidius (2011). "Análisis léxico". Introducción al diseño de compiladores . Temas de pregrado en informática. Londres: Springer. pág. 12. doi :10.1007/978-0-85729-829-4_1. ISBN 978-0-85729-828-7.
6. Lawson (2004) pág. 129
7. Sakarovitch (2009) pág. 228
8. Lawson (2004) pág. 128
9. Grusho, AA (1973). "Distribuciones límite de ciertas características de grafos de autómatas aleatorios". Notas matemáticas de la Academia de Ciencias de la URSS . 4 : 633–637. doi :10.1007/BF01095785. S2CID  121723743.
10. Cai, Xing Shi; Devroye, Luc (octubre de 2017). "La estructura gráfica de un autómata determinista elegido al azar". Random Structures & Algorithms . 51 (3): 428–458. arXiv : 1504.06238 . doi :10.1002/rsa.20707. S2CID  13013344.
11. Carayol, Arnaud; Nicaud, Cyril (febrero de 2012). Distribución del número de estados accesibles en un autómata determinista aleatorio. STACS'12 (29.º Simposio sobre aspectos teóricos de la informática). Vol. 14. París, Francia. pp. 194–205.
12. John E. Hopcroft y Jeffrey D. Ullman (1979). Introducción a la teoría de autómatas, lenguajes y computación . Lectura/MA: Addison-Wesley. ISBN 0-201-02988-X.
13. Rose, Gene F. (1968). "Cierres que preservan la finitud en familias de lenguajes". Revista de Ciencias de la Computación y de Sistemas . 2 (2): 148–168. doi :10.1016/S0022-0000(68)80029-7.
14. Spanier, E. (1969). "Gramáticas y lenguajes". American Mathematical Monthly . 76 : 335–342. doi :10.1080/00029890.1969.12000214. JSTOR  2316423. MR  0241205.
15. Sakarovitch (2009) pág. 105
16. Lawson (2004) pág. 63
17. Esparza Estaun, Francisco Javier; Sickert, Salomon; Blondin, Michael (16 de noviembre de 2016). «Operaciones y pruebas sobre conjuntos: Implementación en DFAs» (PDF) . Autómatas y lenguajes formales 2017/18 . Archivado desde el original (PDF) el 8 de agosto de 2018.
18. Lawson (2004) pág. 46
19. Gold, EM (1978). "Complejidad de la identificación de autómatas a partir de datos dados". Información y control . 37 (3): 302–320. doi :10.1016/S0019-9958(78)90562-4.
20. De Vries, A. (28 de junio de 2014). Autómatas finitos: comportamiento y síntesis. Elsevier. ISBN 9781483297293.
21. Lang, Kevin J. (1992). "Los DFA aleatorios pueden aprenderse aproximadamente a partir de ejemplos uniformes dispersos". Actas del quinto taller anual sobre teoría del aprendizaje computacional - COLT '92 . págs. 45–52. doi :10.1145/130385.130390. ISBN 089791497X.S2CID 7480497  .
22. Oncina, J.; García, P. (1992). "Inferring Regular Languages ​​in Polynomial Updated Time". Reconocimiento de patrones y análisis de imágenes . Serie en Machine Perception and Artificial Intelligence. Vol. 1. págs. 49–61. doi :10.1142/9789812797902_0004. ISBN 978-981-02-0881-3.
23. Lang, Kevin J.; Pearlmutter, Barak A.; Price, Rodney A. (1998). "Resultados de la competencia de aprendizaje DFA de Abbadingo y un nuevo algoritmo de fusión de estados basado en evidencia". Inferencia gramatical (PDF) . Apuntes de clase en informática. Vol. 1433. págs. 1–12. doi :10.1007/BFb0054059. ISBN 978-3-540-64776-8.
24. Más allá de EDSM | Actas del VI Coloquio Internacional sobre Inferencia Gramatical: Algoritmos y Aplicaciones. 23 de septiembre de 2002. pp. 37–48. ISBN 9783540442394.
25. Lucas, SM; Reynolds, TJ (2005). "Aprendizaje de autómatas finitos deterministas con un algoritmo evolutivo de etiquetado de estados inteligente". IEEE Transactions on Pattern Analysis and Machine Intelligence . 27 (7): 1063–1074. doi :10.1109/TPAMI.2005.143. PMID  16013754. S2CID  14062047.
26. Heule, MJH (2010). "Identificación exacta de DFA mediante solucionadores SAT". Inferencia gramatical: resultados teóricos y aplicaciones . Inferencia gramatical: resultados teóricos y aplicaciones. ICGI 2010. Apuntes de clase en informática. Apuntes de clase en informática. Vol. 6339. págs. 66–79. doi :10.1007/978-3-642-15488-1_7. ISBN 978-3-642-15487-4.
27. Heule, Marijn JH ; Verwer, Sicco (2013). "Síntesis de modelos de software utilizando solucionadores de satisfacibilidad". Ingeniería de software empírica . 18 (4): 825–856. doi :10.1007/s10664-012-9222-z. hdl : 2066/103766 . S2CID  17865020.
28. Ulyantsev, Vladimir; Zakirzyanov, Ilya; Shalyto, Anatoly (2015). "Predicados de ruptura de simetría basados ​​en BFS para identificación de DFA". Teoría y aplicaciones de lenguajes y autómatas . Apuntes de clase en informática. Vol. 8977. págs. 611–622. doi :10.1007/978-3-319-15579-1_48. ISBN 978-3-319-15578-4.
29. Davis, Martin; Ron Sigal; Elaine J. Weyuker (1994). Segunda edición: Computabilidad, complejidad y lenguajes y lógica: fundamentos de la informática teórica (2.ª ed.). San Diego: Academic Press, Harcourt, Brace & Company. ISBN 0-12-206382-1.

Referencias

• Hopcroft, John E .; Motwani, Rajeev ; Ullman, Jeffrey D. (2001). Introducción a la teoría de autómatas, lenguajes y computación (2.ª ed.). Boston: Addison Wesley . ISBN 0-201-44124-1.
• Lawson, Mark V. (2004). Autómatas finitos . Chapman y Hall/CRC. ISBN 1-58488-255-7.Zbl 1086.68074  .
• McCulloch, WS; Pitts, W. (1943). "Un cálculo lógico de las ideas inmanentes en la actividad nerviosa". Boletín de biofísica matemática . 5 (4): 115–133. doi :10.1007/BF02478259. PMID  2185863.
• Rabin, MO; Scott, D. (1959). "Autómatas finitos y sus problemas de decisión". IBM J. Res. Dev . 3 (2): 114–125. doi :10.1147/rd.32.0114.
• Sakarovitch, Jacques (2009). Elementos de la teoría de autómatas . Traducido del francés por Reuben Thomas. Cambridge: Cambridge University Press . ISBN 978-0-521-84425-3.Zbl1188.68177  .​
• Sipser, Michael (1997). Introducción a la teoría de la computación . Boston: PWS. ISBN 0-534-94728-X.. Sección 1.1: Autómatas finitos, págs. 31–47. Subsección "Problemas decidibles relacionados con lenguajes regulares" de la sección 4.1: Lenguajes decidibles, págs. 152–155.4.4 DFA solo puede aceptar lenguajes regulares