Polígono de visibilidad

Región poligonal de todos los puntos visibles desde un punto dado en un plano

El polígono de visibilidad se muestra en amarillo. Cuatro obstáculos se muestran en azul.

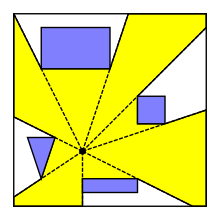
En geometría computacional , el polígono de visibilidad o región de visibilidad para un punto p en el plano entre obstáculos es la región poligonal posiblemente ilimitada de todos los puntos del plano visibles desde p . El polígono de visibilidad también se puede definir para la visibilidad desde un segmento o un polígono. Los polígonos de visibilidad son útiles en robótica , videojuegos y en varios problemas de optimización como el problema de la ubicación de instalaciones y el problema de la galería de arte .

Si el polígono de visibilidad está acotado, entonces es un polígono en forma de estrella . Un polígono de visibilidad está acotado si todos los rayos que salen del punto terminan en algún obstáculo. Este es el caso, por ejemplo, si los obstáculos son los bordes de un polígono simple y p está dentro del polígono. En este último caso, el polígono de visibilidad puede encontrarse en tiempo lineal . ^{[1] [2] [3] [4]}

Definiciones

Formalmente, podemos definir el problema del polígono de visibilidad plana como tal. Sea un conjunto de obstáculos (segmentos o polígonos) en . Sea un punto en que no está dentro de un obstáculo. Entonces, el polígono de visibilidad de puntos es el conjunto de puntos en , tales que para cada punto en , el segmento no interseca ningún obstáculo en . ${\displaystyle S}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle p}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle V}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle q}$ ${\displaystyle V}$ ${\displaystyle pq}$ ${\displaystyle S}$

De igual forma, el polígono de visibilidad de segmento o polígono de visibilidad de arista es la porción visible a cualquier punto a lo largo de un segmento de línea .

Aplicaciones

Los polígonos de visibilidad son útiles en robótica . Por ejemplo, en la localización de robots , un robot que utiliza sensores como un lidar detectará obstáculos que puede ver, lo que es similar a un polígono de visibilidad. ^[5]

También son útiles en los videojuegos , con numerosos tutoriales en línea que explican algoritmos simples para implementarlos. ^{[6] [7] [8]}

Algoritmos para polígonos de visibilidad de puntos

Se han propuesto numerosos algoritmos para calcular el polígono de visibilidad de puntos. Para distintas variantes del problema (por ejemplo, distintos tipos de obstáculos), los algoritmos varían en complejidad temporal.

Algoritmos ingenuos

Los algoritmos ingenuos son fáciles de entender e implementar, pero no son óptimos , ya que pueden ser mucho más lentos que otros algoritmos.

Algoritmo "físico" de proyección de rayos uniforme

En la vida real, un punto luminoso ilumina la región visible para él porque emite luz en todas las direcciones. Esto se puede simular disparando rayos en muchas direcciones. Supongamos que el punto es y el conjunto de obstáculos es . Entonces, el pseudocódigo se puede expresar de la siguiente manera: ${\displaystyle p}$ ${\displaystyle S}$

El algoritmo naive_bad_algorithm( , ) es  := para : ${\displaystyle p}$ ${\displaystyle S}$  ${\displaystyle V}$ ${\displaystyle \emptyset }$   ${\displaystyle \theta =0,\cdots ,2\pi }$ // dispara un rayo con ángulo  := para cada obstáculo en :  := min( , distancia desde el obstáculo en esta dirección) ${\displaystyle \theta }$  ${\displaystyle r}$ ${\displaystyle \infty }$  ${\displaystyle S}$ ${\displaystyle r}$ ${\displaystyle r}$ ${\displaystyle p}$ añadir vértice para retornar ${\displaystyle (\theta ,r)}$ ${\displaystyle V}$   ${\displaystyle V}$

Ahora bien, si fuera posible probar todos los ángulos infinitos, el resultado sería correcto. Lamentablemente, es imposible probar realmente cada dirección debido a las limitaciones de las computadoras. Se puede crear una aproximación lanzando muchos rayos, digamos 50, espaciados uniformemente. Sin embargo, esta no es una solución exacta, ya que dos rayos adyacentes podrían pasar por alto obstáculos pequeños por completo. Además, es muy lento, ya que uno puede tener que lanzar muchos rayos para obtener una solución aproximadamente similar, y el polígono de visibilidad de salida puede tener muchos más vértices de los necesarios.

Lanzamiento de rayos a cada vértice

El algoritmo descrito anteriormente se puede mejorar significativamente tanto en velocidad como en precisión si se tiene en cuenta que basta con disparar rayos a los vértices de cada obstáculo, ya que cualquier curva o esquina a lo largo del límite de un polígono de visibilidad debe deberse a alguna esquina (es decir, un vértice) de un obstáculo.

El algoritmo naive_better_algorithm( , ) es  := para cada obstáculo en : para cada vértice de : ${\displaystyle p}$ ${\displaystyle S}$  ${\displaystyle V}$ ${\displaystyle \emptyset }$  ${\displaystyle b}$ ${\displaystyle S}$ ${\displaystyle v}$ ${\displaystyle b}$ // dispara un rayo desde a  := distancia desde a  := ángulo de con respecto a para cada obstáculo en :  := min( , distancia desde a ) ${\displaystyle p}$ ${\displaystyle v}$  ${\displaystyle r}$ ${\displaystyle p}$ ${\displaystyle v}$  ${\displaystyle \theta }$ ${\displaystyle v}$ ${\displaystyle p}$  ${\displaystyle b'}$ ${\displaystyle S}$ ${\displaystyle r}$ ${\displaystyle r}$ ${\displaystyle p}$ ${\displaystyle b'}$ añadir vértice para retornar ${\displaystyle (\theta ,r)}$ ${\displaystyle V}$   ${\displaystyle V}$

El algoritmo anterior puede no ser correcto. Ver la discusión en Discusión.

La complejidad temporal de este algoritmo es . Esto se debe a que el algoritmo dispara un rayo a cada uno de los vértices y, para comprobar dónde termina el rayo, tiene que comprobar la intersección con cada uno de los obstáculos. Esto es suficiente para muchas aplicaciones sencillas, como los videojuegos, y como tal, muchos tutoriales en línea enseñan este método. ^[8] Sin embargo, como veremos más adelante, hay algoritmos más rápidos (o incluso más rápidos si el obstáculo es un polígono simple o si hay un número fijo de agujeros poligonales). ${\displaystyle O(n^{2})}$ ${\displaystyle n}$ ${\displaystyle O(n)}$ ${\displaystyle O(n\log n)}$

Algoritmos óptimos para un punto en un polígono simple

Un polígono de visibilidad para un punto en el centro (mostrado en blanco) dentro de un polígono simple, delineado en negro.

Dado un polígono simple y un punto , un algoritmo de tiempo lineal es óptimo para calcular la región en que es visible desde . Este algoritmo fue propuesto por primera vez en 1981. ^[2] Sin embargo, es bastante complicado. En 1983, se propuso un algoritmo conceptualmente más simple, ^[3] que tenía un error menor que se corrigió en 1987. ^[4] ${\displaystyle {\mathcal {P}}}$ ${\displaystyle p}$ ${\displaystyle {\mathcal {P}}}$ ${\displaystyle p}$

El último algoritmo se explicará brevemente aquí. Simplemente recorre el límite del polígono , procesando los vértices en el orden en que aparecen, mientras mantiene una pila de vértices donde es la parte superior de la pila. La pila constituye los vértices encontrados hasta ahora que son visibles para . Si, más tarde durante la ejecución del algoritmo, se encuentran algunos vértices nuevos que oscurecen parte de , entonces los vértices oscurecidos en se extraerán de la pila. Para cuando el algoritmo finalice, consistirá en todos los vértices visibles, es decir, el polígono de visibilidad deseado. En 2014 se publicó una implementación eficiente. ^[9] ${\displaystyle {\mathcal {P}}}$ ${\displaystyle {\mathcal {S}}=s_{0},s_{1},\cdots ,s_{t}}$ ${\displaystyle s_{t}}$ ${\displaystyle p}$ ${\displaystyle {\mathcal {S}}}$ ${\displaystyle {\mathcal {S}}}$ ${\displaystyle {\mathcal {S}}}$

Algoritmos óptimos para un punto en un polígono con agujeros

Para un punto de un polígono con agujeros y vértices en total, se puede demostrar que, en el peor de los casos, un algoritmo es óptimo. Dicho algoritmo se propuso en 1995 junto con su prueba de optimalidad. ^[10] Sin embargo, se basa en el algoritmo de triangulación de polígonos en tiempo lineal de Chazelle, que es extremadamente complejo. ${\displaystyle h}$ ${\displaystyle n}$ ${\displaystyle \Theta (n+h\log h)}$

Algoritmos óptimos para un punto entre segmentos

Segmentos que no se intersecan excepto en sus puntos finales

Un polígono de visibilidad para un punto en el centro (mostrado en blanco) entre un conjunto de segmentos de línea arbitrarios en el plano, a los que se les permite intersecarse solo en sus puntos finales, actuando como obstáculos (mostrados en negro).

Para un punto entre un conjunto de segmentos que no se intersecan excepto en sus puntos finales, se puede demostrar que, en el peor de los casos, un algoritmo es óptimo. Esto se debe a que un algoritmo de polígono de visibilidad debe generar los vértices del polígono de visibilidad en orden ordenado, por lo que el problema de la clasificación se puede reducir al cálculo de un polígono de visibilidad. ^[11] ${\displaystyle n}$ ${\displaystyle \Theta (n\log n)}$

Tenga en cuenta que cualquier algoritmo que calcule un polígono de visibilidad para un punto entre segmentos se puede utilizar para calcular un polígono de visibilidad para todos los demás tipos de obstáculos poligonales, ya que cualquier polígono se puede descomponer en segmentos.

Divide y vencerás

En 1987 se propuso un algoritmo de divide y vencerás para calcular el polígono de visibilidad ^{. [12]}

Barrido angular

^{En 1985 [13]} y 1986 ^[11] se propuso un algoritmo de barrido angular , es decir, de barrido de plano rotacional para calcular el polígono de visibilidad . La idea es primero ordenar todos los puntos finales del segmento por ángulo polar y luego iterarlos en ese orden. Durante la iteración, la línea de eventos se mantiene como un montón . En 2014 se publicó una implementación eficiente. ^[9]

Segmentos generalmente intersecantes

Para un punto entre segmentos que generalmente se intersecan, el problema del polígono de visibilidad es reducible, en tiempo lineal, al problema de la envolvente inferior . Por el argumento de Davenport-Schinzel , la envolvente inferior en el peor de los casos tiene número de vértices, donde es la función de Ackermann inversa . John Hershberger creó en 1989 un algoritmo óptimo de divide y vencerás en el peor de los casos que se ejecuta en el tiempo. ^[14] ${\displaystyle \Theta (n\alpha (n))}$ ${\displaystyle \alpha (n)}$ ${\displaystyle \Theta (n\log n)}$

Referencias

1. Franco P. Preparata y Michael Ian Shamos (1985). Geometría computacional: una introducción . Springer-Verlag . ISBN 0-387-96131-3. 1ª edición; 2ª impresión, corregida y ampliada, 1988: ISBN 3-540-96131-3 ; traducción rusa, 1989: ISBN 5-03-001041-6 .  
2. El Gindy, Hossam; Avis, David (1981). "Un algoritmo lineal para calcular el polígono de visibilidad a partir de un punto". Journal of Algorithms . 2 (2): 186–197. doi :10.1016/0196-6774(81)90019-5.
3. Lee, DT (mayo de 1983). "Visibilidad de un polígono simple". Visión artificial, gráficos y procesamiento de imágenes . 22 (2): 207–221. doi :10.1016/0734-189X(83)90065-8.
4. Joe, Barry; Simpson, RB (1987). "Correcciones al algoritmo de polígono de visibilidad de Lee". BIT Numerical Mathematics . 27 (4): 458–473. doi :10.1007/BF01937271. S2CID  19112466.
5. Guibas, Leonidas; Motwani, Rajeev; Raghavan, Prabhakar (1992). El problema de localización de robots en dos dimensiones . Simposio ACM-SIAM sobre algoritmos discretos. Sociedad de Matemáticas Industriales y Aplicadas.
6. Liow, Nicklaus. "SIGHT & LIGHT: cómo crear efectos de visibilidad y sombras 2D para tu juego" . Consultado el 9 de mayo de 2014 .
7. Patel, Amit (5 de julio de 2012). «Algoritmo de visibilidad 2D» . Consultado el 9 de mayo de 2014 .
8. Patel, Amit (5 de julio de 2012). «Blobs in Games: 2d Visibility» (Blobs en los juegos: visibilidad en 2D) . Consultado el 9 de mayo de 2014 .
9. Bungiu, Francisc; Hemmer, Michael; Hershberger, John; Huang, Kan; Kröller, Alexander (2014). "Cálculo eficiente de polígonos de visibilidad". arXiv : 1403.3905 [cs.CG].
10. Heffernan, Paul; Mitchell, Joseph (1995). "Un algoritmo óptimo para calcular la visibilidad en el plano" (PDF) . SIAM Journal on Computing . 24 (1): 184–201. doi :10.1137/S0097539791221505. hdl : 1813/8838 .
11. Suri, Subhash; O'Rourke, Joseph (1986). Algoritmos óptimos en el peor de los casos para construir polígonos de visibilidad con agujeros . Simposio sobre geometría computacional. ACM . págs. 14-23. doi :10.1145/10515.10517.
12. Arkin, E .; Mitchell, Joseph (1987). Un algoritmo de visibilidad óptima para un polígono simple con agujeros en forma de estrella (informe técnico). Investigación de operaciones e ingeniería industrial de la Universidad de Cornell. 746.
13. Asano, Tetsuo (1985). Un algoritmo eficiente para encontrar el polígono de visibilidad para una región poligonal con agujeros . Instituto de Ingenieros en Electrónica, Información y Comunicación. Vol. 68. págs. 557–559.
14. Hershberger, John (1989). "Encontrar la envolvente superior de segmentos de línea en el tiempo". Information Processing Letters . 33 (4): 169–174. doi :10.1016/0020-0190(89)90136-1. ${\displaystyle n}$ ${\displaystyle O(n\log n)}$

Enlaces externos

• http://web.informatik.uni-bonn.de/I/GeomLab/VisPolygon/index.html.en (visibilidad en polígonos simples - applets)

Software

• VisiLibity: una biblioteca C++ gratuita de código abierto para cálculos de visibilidad en entornos poligonales planos.
• visibilidad-polygon-js: una biblioteca de Javascript de dominio público para calcular un polígono de visibilidad para un punto entre segmentos utilizando el método de barrido angular.